Время полета

При выводе уравнения траектории показано, что абсцисса любой точки траектории

х = v₀t cos θ₀ (рис. 4),

откуда

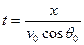
Из записанного уравнения можно сделать вывод, что если v ₀ и θ₀ заданы, то время полета снаряда до любой точки траектории пропорционально горизонтальному перемещению снаряда. Например, вершина траектории лежит над серединой полной горизонтальной дальности полета, следовательно, и время полета снаряда от точки вылета до вершины равно времени полета от вершины до точки падения и составляет половину полного времени полета t_c.

Для того чтобы определить полное время полета, необходимо в качестве абсциссы принять полную горизонтальную дальность

.

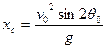Тогда

. (1.5)

Из уравнения 1.5 видно, что полное время полета, как и полная горизонтальная дальность и высота траектории, зависит от начальной скорости и угла бросания. Однако при совместном решении уравнений 1.5 и 1.3 можно прийти к выводу, что полное время полета в конечном счете зависит только от высоты траектории.

Рнс. 8. Траектории снаряда при одинаковом времени полета:

θ₁ = 65°, v ₀₁ = 338 м/с; θ₂ = 76°, v ₀₂=328 м/с; х_с1= 8850 м, х_с2= 4420 м, t_c1=t_c2= 60 с

Из уравнения 1.3

Подставив в формулу 1.5 вместо v₀ правую часть записанного равенства, получим

. (1.6)

Таким образом, для того чтобы определить полное время полета, достаточно знать высоту траектории.

Пример. Y_s = 4410 м, t_c =?

t_c = 0,903 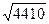= 0,903*66,41 ≈ 60 с.

Формула 1.6 дает возможность сделать важный практический вывод о том, что если высоты различных траекторий равны (рис. 8), то независимо от величин v₀, θ₀ и дальности полета время полета для всех таких траекторий будет одинаковым. Это положение используется при подготовке данных для стрельбы.

Лекція 9

Тема 4. Заняття 1. Рух снаряда в повітрі

1. Поняття про силу опору повітря.

2. Величина сили опору повітря.

Дата добавления: 2014-01-07