Начало жесткости траектории. Поправка угла прицеливания на угол места цели

Исследования показывают, что при стрельбе в воздухе при небольших углах бросания (до 15°) для равных осевых расстояний (ОЦ = ОЦ₀) понижения снаряда под линией бросания равны (рис. 28).

Это положение получило наименование «Начало Сан-Ро-берто» (в честь итальянского артиллериста Сан-Роберто).

Из этого положения следует, что при небольших углах бросания траектории имеют одинаковые очертания независи­мо от угла бросания, или при повороте траектории около точки вылета (в плоскости стрельбы) очертания ее практически не изменяются, а это в свою очередь дает основание утверждать, что при малых углах бросания углы прицеливания для достижения одинаковых наклонных дальностей не зависят от углов места цели (рис. 29). Это положение и принято называть началом жесткости траектории. Применение начала жесткости траектории при допущении, что при малых углах места цели наклонная дальность до цели равна топо-гпафической дальности, и дает основание считать, что для этих условий

Δφ = ε

Рис.28. Начало Сан – Роберто

Рис. 29. Начало жесткости траектории:

ОЦ ₀ = ОЦ; α = α₀

При углах места цели более 10 делений угломера и углах прицеливания более 150—200 тысячных поправка на превышение цели Δφ не будет равна углу места цели ε, так как, во-первых, при больших углах бросания даже незначительному изменению угла прицелива­ния сопутствует заметное изменение кривизны траектории и, во-вторых, при больших углах места цели наклонная (фактичеекая) дальность до цели значительно отличается от горизонтальной (топографической) дальности.

Покажем это для случая, когда цель выше горизонта орудия (угол места цели ε положительный), а угол прицеливания α меньше 45° (рис. 30).

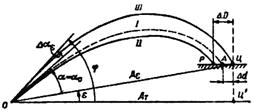
Рис. 30. Поправка угла прицеливания на угол места

цели (цель выше горизонта орудия, α<45°)

Если произвести выстрел при угле возвышения α₀ + α, то, в силу того что наклонная дальность ОЦ больше горизонтальной ОЦ', даже при условии полной жесткости траекто­рии снаряд не долетит до цели на отрезок Δ d (ОА = ОЦ'). Но при повороте траектории на угол ε (увеличении угла возвышения) увеличится и кривизна траектории и снаряд полетит не по траектории І, а по траектории II и упадет не в точке А, а в точке Р, т. е. не долетит до цели на величину Δ D> Δ d.

Чтобы траектория прошла через точку цели Ц, необходимо увеличить угол прицеливания на угол Δα_ε (траектория III).

Величину этого угла и называют поправкой угла прицеливания на угол места цели.

Поправка прицела на превышение цели в этом случае будет равна

Δφ = ε +Δα_ε. (1.13)

Знак поправки Δα_ε зависит от знака угла места цели и вида стрельбы.

При настильной и навесной стрельбе поправка угла при­целивания на угол места цели имеет знак угла места цели; поэтому поправка прицела на превышение цели Δφ при углах возвышения меньше 45° по абсолютной величине всегда больше ε.

При мортирной стрельбе поправка угла прицеливания на угол места цели имеет знак, противоположный знаку угла места цели.

На рис. 27 показано, что в этом случае и суммарная поправка прицела на превышение Δφ имеет знак, противоположный знаку угла места цели; поэтому из уравнения 1.13 следует, что при углах возвышения, больших 45°, поправка угла прицеливания на угол места цели по абсолютной величине всегда больше угла места цели.

Итак, в общем случае для учета превышения цели угол возвышения должен быть равен

φ == α₀ + ε +Δα_ε. (1.14)

где α₀ —угол прицеливания, соответствующий топографической (горизонтальной) дальности до цели;

ε — угол места цели (определяют расчетом);

Δα_ε — поправка угла прицеливания на угол места цели (определяют по Таблицам стрельбы).

Последние две величины берутся с учетом их знаков. В Таблицах стрельбы минометов и Таблицах стрельбы (издания девятое дополненное и десятое) 122 -мм гаубицы обр. 1938 г. приводятся суммарные поправки на превышение цели, т. е. величины ε +Δα_ε.. Для 122 -мм гаубицы эта поправка (Δ П_ε) рассчитана на превышение, равное 100 м, и помещена в основной таблице; в таблицах стрельбы минометов она приведена для различных значений превышения и помещена в специальной таблице.

Лекція 12

Тема 5. Заняття 1. Вплив балістичних умов на політ снаряда

1. Табличні умови стрільби.

2. Вплив відхилення початкової швидкості.

3. Вплив відхилення температури заряду.

4. Вплив відхилення ваги снаряда.

5. Вплив відхилення форми і стану поверхні снаряда.

Дата добавления: 2014-01-07