
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Застосування похідної до дослідження функції і побудови графіка
|
|
|
|
План повного дослідження функції
1) Область визначення
2) Точки перетину з осями координат (знаки функції), парність, періодичність.
3) Неперервність, точки розриву (їхній рід). Вертикальні асимптоти.
4) Монотонність і точки екстремуму.
5) Опуклість і точки перегину
6) Дослідження на нескінченості: горизонтальні та похилі асимптоти.
7) Побудова графіку
8) Область значень функції і обмеженість на ОДЗ.
Дослідження на монотонність (проміжки зростання, спадання)
Теорема 1. Якщо функція f неперервна на [a,b], диференційована на (а;b)

 , x є(а; b) то f зростаюча (спадна) на [а,b].
, x є(а; b) то f зростаюча (спадна) на [а,b].
Доведення. Нехай 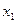 <
<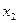 ,
, 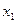 ,
,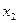 є [а,b]. Тоді за теоремою Лагранжа існує точка с є (
є [а,b]. Тоді за теоремою Лагранжа існує точка с є (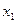 ,
,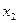 ) така, що
) така, що 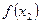 -
-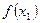 =
=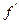 (с) (
(с) (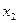 -
-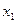 ).
).
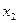 -
-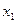 >0, то знак правої частини залежить від знаку
>0, то знак правої частини залежить від знаку 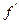 (с). Якщо
(с). Якщо 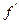 (с)
(с) 0, то
0, то
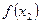 -
-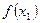
 0
0 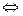
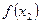

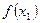 , тобто функція зростаюча на [a,b]. Якщо
, тобто функція зростаюча на [a,b]. Якщо 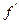 (с)
(с) 0, то
0, то 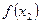 -
-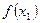
 0
0 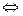
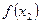

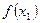 , тобто функція cпадна на [a,b].
, тобто функція cпадна на [a,b].
Приклад.  =
=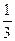
 -
- 
 +2x, ОДЗ: х є R
+2x, ОДЗ: х є R

 =
= -3x +2. Знайдемо проміжки сталих знаків
-3x +2. Знайдемо проміжки сталих знаків  . Оскільки
. Оскільки  елементарна функція, то вона може змінювати знаки тільки в точках, де вона перетворюється в нуль або не існує. Її ОДЗ: х є R. Знайдемо точки, в яких вона рівна нулю:
елементарна функція, то вона може змінювати знаки тільки в точках, де вона перетворюється в нуль або не існує. Її ОДЗ: х є R. Знайдемо точки, в яких вона рівна нулю:
|
 =0
=0
 -3x +2 =0
-3x +2 =0
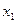 =1;
=1; 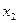 =2.
=2.
Нанесемо на числову пряму область визначення початкової функції y, і точки, де її похідна  може змінювати знак і визначимо знаки
може змінювати знак і визначимо знаки  . Отже, f зростаюча на (-
. Отже, f зростаюча на (-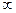 ; 1] і на [2;+
; 1] і на [2;+ ), f спадна на [1;2].
), f спадна на [1;2].
Дослідження на екстремуми
Точка  називається точкою максимуму функції f на множині А, якщо в цій точці функція приймає найбільше значення:
називається точкою максимуму функції f на множині А, якщо в цій точці функція приймає найбільше значення: 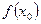

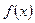 , x є А (перший малюнок).
, x є А (перший малюнок).
Точка  називається точкою мінімуму функції f на множині А, якщо в цій точці функція приймає найменше значення:
називається точкою мінімуму функції f на множині А, якщо в цій точці функція приймає найменше значення: 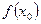

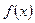 , x є А (другий малюнок).
, x є А (другий малюнок). 

 Точки максимуму і мінімуму на множині А називаються точками екстремуму функції f на множині А. Такі екстремуми ще називають абсолютними екстремумами на множині А.
Точки максимуму і мінімуму на множині А називаються точками екстремуму функції f на множині А. Такі екстремуми ще називають абсолютними екстремумами на множині А.
Якщо точка  є точкою екстремуму (max або min) функції f в деякому своєму околі, то
є точкою екстремуму (max або min) функції f в деякому своєму околі, то  називається точкою локального або місцевого екстремуму (max або min) функції f.
називається точкою локального або місцевого екстремуму (max або min) функції f.
На третьому малюнку точки a,b,c,d є точками локальних екстремумів, точки k,n є точками абсолютних екстремумів функції на області визначення.
Надалі розглядаємо в основному локальні екстремуми.
Теорема 2 (необхідна умова екстремуму). Якщо точка  є точкою локального екстремуму f то похідна в цій точці не існує або дорівнює 0.
є точкою локального екстремуму f то похідна в цій точці не існує або дорівнює 0.
Доведення. Нехай  є точкою локального мінімуму f і існує похідна
є точкою локального мінімуму f і існує похідна  =
= .
.
Розглянемо окремо ліву і праву границю:
 , бо чисельник
, бо чисельник  0, а знаменник < 0;
0, а знаменник < 0; 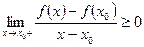 , бо чисельник залишається
, бо чисельник залишається  0, а знаменник вже > 0. Оскільки ця границя існує, то це можливо тільки коли ліва і права границі рівні нулю, тобто
0, а знаменник вже > 0. Оскільки ця границя існує, то це можливо тільки коли ліва і права границі рівні нулю, тобто  =0.
=0.
Означення. Точки в яких похідна дорівнює нулю або не існує називають критичними точками. Ці точки є підозрілими на екстремум.
Теорема 3 (перша достатня умова екстремуму). Якщо f неперервна в деякому околі т. і при переході через цю точку похідна
і при переході через цю точку похідна 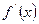 змінює знак, то
змінює знак, то  є точкою екстремуму функції f.
є точкою екстремуму функції f.
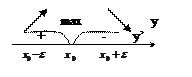 Доведення на малюнку:
Доведення на малюнку:

|
Приклад.  ОДОДЗ: x єR
ОДОДЗ: x єR
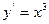 . Знаходимо критичні точки: ОДЗ: x є R, тобто
. Знаходимо критичні точки: ОДЗ: x є R, тобто  існує всюди.
існує всюди.
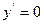

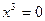 х=0 – точка мінімуму,
х=0 – точка мінімуму,  .
.
Теорема 4 (друга достатня умова екстремуму). Нехай функція двічі диференційована в деякому околі точки  і
і  =0, а
=0, а  >0 (
>0 ( <0), то
<0), то  є точкою мінімуму (максимуму) функції.
є точкою мінімуму (максимуму) функції.
Доведення. За теоремою Тейлора в достатньо малому околі точки  :
: 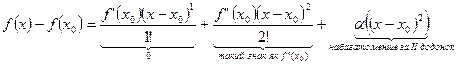 . Отже, якщо
. Отже, якщо  >0, то
>0, то 
 в деякому околі точки
в деякому околі точки  , тобто
, тобто  є точкою мінімуму функції.
є точкою мінімуму функції.
Приклад. y=3x- D(y): x Є R
D(y): x Є R

 D(
D( ): x є R
): x є R  3-3
3-3 =0 x=
=0 x= 1-критичні точки
1-критичні точки
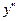 = - 6х
= - 6х 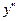 (1)= - 6 < 0, то х=1 є точкою максимуму функції, y(1)=2,
(1)= - 6 < 0, то х=1 є точкою максимуму функції, y(1)=2,
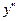 (-1)= 6 > 0, то х= -1 є точкою мінімуму функції, y(-1)= -2.
(-1)= 6 > 0, то х= -1 є точкою мінімуму функції, y(-1)= -2.
Дослідження на опуклість
 Нехай функція f неперервна на (а,b)
Нехай функція f неперервна на (а,b)
Функція називається опуклою вниз (вгнутою) на інтервалі (а,b), якщо для будь-яких точок  із (а,b) графік функції на проміжку (
із (а,b) графік функції на проміжку ( ) лежить не вище від січної, що проходить через точки з абсцисами
) лежить не вище від січної, що проходить через точки з абсцисами  . Позначається: f
. Позначається: f на (а,b).
на (а,b).
Функція буде строго опуклою вниз на (а,b), якщо – графік на ( ) лежить нижче від січної.
) лежить нижче від січної.
Функція називається опуклою вверх (опуклою) на інтервалі (а,b), якщо для будь-яких точок  із (а,b) графік функції на проміжку (
із (а,b) графік функції на проміжку ( ) лежить не нижче від січної, що проходить через точки з абсцисами
) лежить не нижче від січної, що проходить через точки з абсцисами  . Позначається: f
. Позначається: f 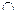 (а,b).
(а,b).
Функція буде строго опуклою вверх на (а,b), якщо – графік на ( ) лежить вище від січної.
) лежить вище від січної.
Якщо функція неперервна в деякому околі точки  і при переході через точку
і при переході через точку  функція змінює опуклість то ця точка називається точкою перегину функції.
функція змінює опуклість то ця точка називається точкою перегину функції.
Приклади. 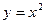 - опукла вниз на R. y=ln x – опукла вверх на (0,
- опукла вниз на R. y=ln x – опукла вверх на (0,  ).
).
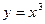 - опукла вверх на (
- опукла вверх на (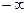 ,0], опукла вниз на [0,
,0], опукла вниз на [0,  ), і точка х=0 є її точкою перегину.
), і точка х=0 є її точкою перегину.

Розглянемо графік опуклої вниз функції. Нехай  . Побудуємо дотичні в цих точках. Позначимо кути, які дотичні утворюють з додатнім напрямком Ох
. Побудуємо дотичні в цих точках. Позначимо кути, які дотичні утворюють з додатнім напрямком Ох 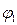 ,
,  ,
, 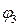 відповідно.
відповідно. 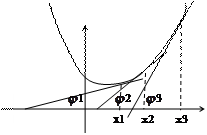
З малюнка бачимо, що кут зростає при зростанні х:
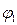 <
< <
<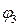 (кут вважаємо з проміжку [
(кут вважаємо з проміжку [ ]).
]).
Функція tg х зростає на ( ) то
) то
tg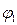 <tg
<tg <tg
<tg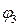 , тобто
, тобто  . А це означає, що
. А це означає, що  зростаюча функція на даному проміжку.
зростаюча функція на даному проміжку.
 Для опуклої вверх і диференційованої на (а,b) функції її похідна
Для опуклої вверх і диференційованої на (а,b) функції її похідна  на (а,b).
на (а,b).
Отже, для того щоб дослідити функцію на опуклість потрібно дослідити на монотонність її похідну  , а для цього шукають
, а для цього шукають  , тобто
, тобто 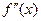 . Тому справедливі теореми.
. Тому справедливі теореми.
Т.1. Якщо f двічі диференційована на (а,b) і 1)  (x)>0 на (а,b) то f опукла вниз на (а,b);
(x)>0 на (а,b) то f опукла вниз на (а,b);
2)  (х)<0 на (а,b) то f опукла вниз на (а,b).
(х)<0 на (а,b) то f опукла вниз на (а,b).
Т.2. Якщо точка є (а,b), функція f неперервна на (a,b) і існує друга похідна
є (а,b), функція f неперервна на (a,b) і існує друга похідна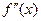 зліва і справа від т.
зліва і справа від т.  , яка при переході через точку
, яка при переході через точку  змінює знак, то
змінює знак, то  є точкою перегину функції f.
є точкою перегину функції f.
Приклад1. Дослідити на опуклість функцію  .
.
Функція елементарна, тому неперервна на своїй області визначення, тобто на R.


 – не існує при х=0.
– не існує при х=0.
|
 – немає розв’язків.
– немає розв’язків.
Наносимо на числову пряму область визначення початкової функції.
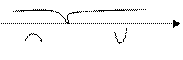 Приклад 2. Дослідити на опуклість функцію
Приклад 2. Дослідити на опуклість функцію  .
.
|
тобто на R. 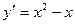
 – існує завжди.
– існує завжди.  .
.
Дослідження на асимптоти.

Означення. Асимптотою графіка функції f(х) називається пряма, до якої наближається точка графіка функції при нескінченному віддаленні від початку координат: d(M, l) .
.
Асимптоти можуть бути вертикальні, горизонтальні і похилі.
1) Вертикальна пряма з рівнянням 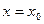 буде вертикальною асимптотою графіка функції f, якщо в точці
буде вертикальною асимптотою графіка функції f, якщо в точці  є нескінченний розрив, тобто хоча б одна ліва або права границя в цій точці є нескінченністю:
є нескінченний розрив, тобто хоча б одна ліва або права границя в цій точці є нескінченністю: 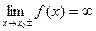 .
.
Нехай точка графіка М(х,у), y=f(x). Тоді при  d=x-
d=x-
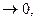 а OM=
а OM=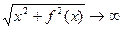 .
.
Приклад. Функція  . ОДЗ:
. ОДЗ: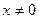 . В точці 0 – розрив.
. В точці 0 – розрив.  – нескінченний розрив (ІІ рід). Вертикальна асимптота х=0. (В такому випадку корисно знайти окремо ліву і праву границю функції в точці розриву.)
– нескінченний розрив (ІІ рід). Вертикальна асимптота х=0. (В такому випадку корисно знайти окремо ліву і праву границю функції в точці розриву.)
2) Горизонтальна пряма з рівнянням у=b буде асимптотою графіка функції f, якщо  (границя може бути тільки на одній з нескінченостей на +
(границя може бути тільки на одній з нескінченостей на +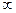 чи на -
чи на -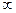 ).
).
Нехай точка графіка М(х,у), y=f(x). Тоді при 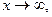 d=f(x)-b
d=f(x)-b 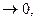 а OM=
а OM=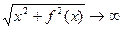 .
.
 Приклад.
Приклад. 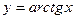
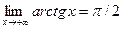 ,
, 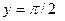 – горизонтальна асимптота на
– горизонтальна асимптота на  .
.
 ,
,
 – горизонтальна асимптота на
– горизонтальна асимптота на 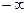 .
.
3) Похила пряма з рівнянням y=kx+b є асимптотою графіка функції f(x), якщо існують і є числами границі  ,
,  (границі можуть бути тільки на одній з нескінченостей на +
(границі можуть бути тільки на одній з нескінченостей на +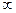 чи на -
чи на -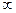 ).
).
Приклад. Дослідити на асимптоти на нескінченності функцію 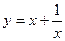 .
.
ОДЗ: 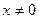 . Можна шукати границю на нескінченності.
. Можна шукати границю на нескінченності.  – не число, немає горизонтальної асимптоти. Але може бути похила.
– не число, немає горизонтальної асимптоти. Але може бути похила.
 =1+0=1 – число, k=1,
=1+0=1 – число, k=1,
 – число, b=0. Отже, у=х – похила асимптота на
– число, b=0. Отже, у=х – похила асимптота на 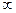 , тобто одночасно на +
, тобто одночасно на +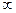 і на -
і на -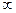 .
.
Повне дослідження функції
Приклад. Дослідити функцію і побудувати її графік 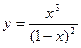 .
.
1) ОДЗ: 1-x 0
0
x 1
1
ОДЗ: х є (-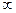 ; 1)
; 1)  (1;
(1; 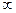 ).
).
2) Функція загального вигляду (ні парна ні непарна), тому що ОДЗ не симетрична відносно точки 0. Неперіодична бо область визначення неперіодична (розрив періодично не повторюється).
х=0 у=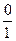 =0 А(0;0) у=0
=0 А(0;0) у=0  <0 x=0 та ж точка А(0;0).
<0 x=0 та ж точка А(0;0).
Знаки функції. Функція елементарна, тому може змінювати знак тільки в точках, де вона дорівнює нулю, або не існує. Нанесемо на числову пряму область визначення і точку, де функція дорівнює нулю:

|
 . Розрив х=1
. Розрив х=1
 - розрив 2-го роду (нескінченний), тому є вертикальна асимптота в точці 1, х=1 – рівняння вертикальної асимптоти.
- розрив 2-го роду (нескінченний), тому є вертикальна асимптота в точці 1, х=1 – рівняння вертикальної асимптоти.
4) 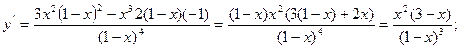
Критичні точки:
|
 ОДЗ
ОДЗ 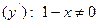 х
х 1
1
х=1- критична точка
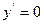 х=0; х=3- критичні точки.
х=0; х=3- критичні точки.

|
5)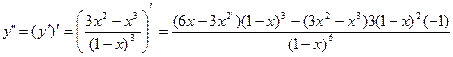 =
=
=
Критичні точки: х=1, 6х=0, х=0, т.х=0 є точкою перегину, у(0)=0.
6)  немає горизонтальної асимптоти, але може бути похила.
немає горизонтальної асимптоти, але може бути похила.
 k=
k=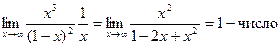 . b=
. b=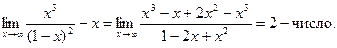 Отже, є похила асимптота y=x+2 на
Отже, є похила асимптота y=x+2 на і на
і на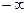 .
.
7. Графік функції.
8)  , як бачимо з графіка.
, як бачимо з графіка.
Функція необмежена на області визначення.
Дослідження функції на найменше і найбільше значення на відрізку
Якщо функція неперервна на [а,b] то за теоремою Вейєрштраса існує найбільше і найменше значення на цьому відрізку, тобто існують точки  такі, що
такі, що
 , х є
, х є 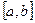 . Із теорем про монотонність і екстремуми отримуємо наступний план дослідження функції на найменше та найбільше значення на відрізку.
. Із теорем про монотонність і екстремуми отримуємо наступний план дослідження функції на найменше та найбільше значення на відрізку.
План
1. Знайти  і її критичні точки (точки, в яких похідна не існує або дорівнює нулю).
і її критичні точки (точки, в яких похідна не існує або дорівнює нулю).
2. Знайти значення функції f в цих точках і на кінцях відрізка.
3. Порівняти знайдені значення, вибрати найменше і найбільше.
Приклад. Дослідити функцію  на абсолютні екстремуми (найбільше і найменше значення) на
на абсолютні екстремуми (найбільше і найменше значення) на  .
.
ОДЗ: D(y) є R. Функція елементарна, тому неперервна на R і, зокрема на [0,2].
 ОДЗ: D(y) є R
ОДЗ: D(y) є R  -1=0
-1=0  =1 x=
=1 x=  1 -1
1 -1  -відкидаємо.
-відкидаємо.
 - найменше значення.
- найменше значення.
y(0)=0
y(2)=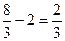 - найбільше значення.
- найбільше значення.
Можна також вказати область значень функції на даному проміжку – [-2/3;2/3].
Зауваження. Якщо треба дослідити функцію на найбільше та найменше значення на скінченому інтервалі (а,b), чи на нескінченному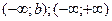 , то в плані замість значень функції на кінцях проміжку шукають відповідні односторонні границі: замість f(a) шукають f(a+)=
, то в плані замість значень функції на кінцях проміжку шукають відповідні односторонні границі: замість f(a) шукають f(a+)= f(x), замість f(b) шукають f(b-). Так можна знайти область значень функції на проміжку, бо абсолютні екстремуми не обов’язково існують в даному випадку.
f(x), замість f(b) шукають f(b-). Так можна знайти область значень функції на проміжку, бо абсолютні екстремуми не обов’язково існують в даному випадку.
Застосування похідної до розв’язування прикладних задач на екстремум деяких величин
1. Виражають дану величину через інші величини з умови задачі так, щоб вона була функцією тільки від однієї змінної (якщо це можливо).
2. Визначають проміжок зміни цієї змінної.
3. Досліджують цю функцію на найбільше і найменше значення на проміжку.
Задача. Потрібно побудувати прямокутну площадку, використавши а метрів сітки, біля стіни так, щоб з одного боку вона прилягала до стіни, а з інших трьох була огороджена сіткою. При якому співвідношенні сторін площа такої площадки буде найбільшою?
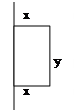 S=xу – функція двох змінних. L=x+у+x=a у=a-2x
S=xу – функція двох змінних. L=x+у+x=a у=a-2x
S=x (a-2x) – функція однієї змінної х; х є  .
.
S=x (a-2x)=а x - 2x S’=a-4x, x є R, S’=0 a- 4x=0 x=
S’=a-4x, x є R, S’=0 a- 4x=0 x=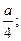
x=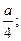 S(
S( )=
)= – найбільше значення. S(0)=0, S(
– найбільше значення. S(0)=0, S( . Знайдемо другу сторону прямокутника: у = a -
. Знайдемо другу сторону прямокутника: у = a -  . Співвідношення сторін:
. Співвідношення сторін:  .
.
Відповідь. Найбільша площа буде дорівнювати  , якщо сторона паралельна до стіни в два рази більша від іншої сторони.
, якщо сторона паралельна до стіни в два рази більша від іншої сторони.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1356; Нарушение авторских прав?; Мы поможем в написании вашей работы!