Рівняння Шредінгера

1⁰. У квантовій механіці постає важлива проблема про відшукання такого рівняння, яке б мало таке саме значення, як рівняння руху Ньютона для класичної механіки. Положення частинки в квантовій механіці описується заданням псі-функції, тому рівняння має бути хвильовим.

Основне рівняння квантової механіки було знайдено у 1926 році Е.Шредінгером. Воно постулюється. Фундаментальне лінійне диференційне рівняння нерелятивістської квантової механіки, яким описується динамічний стан мікросистеми називається рівнянням Шредінгера. Його найзагальніший вигляд такий:

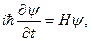(7.3)

де Н – оператор Гамільтона системи, оператор повної енергії

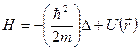
У вужчому розумінні - це основне часове рівняння нерелятивістської динаміки мікросистеми, яка перебуває в зовнішньому полі:

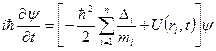, (7.4)

де 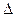– оператор Лапласа (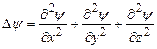), 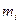– маса і -ої частинки, 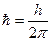, , U – потенціальна енергія нерелятивістських частинок системи.

2⁰. Важливо також знайти стаціонарні розв’язки рівняння Шредінгера, які не містять часу. Якщо потенціальна енергія U не залежить явно від часу, то стаціонарні стани описуються стаціонарним рівнянням Шредінгера:

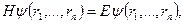(7.5)

де Е - повна енергія системи. Хвильова функція 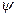в цьому рівнянні є функцією координат. Окремим випадком рівняння є рівняння Шредінгера для безспінової частинки, яка міститься в певному силовому полі:

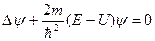(7.6)

Для цілком вільної частинки (U = 0)

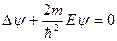(7.7)

. Функції 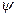, які задовольняють рівнянню Шредінгера при заданому 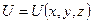називаються власними функціями. Вони існують (при вимозі однозначності, скінченності і неперервності) лише при певних значеннях Е, які називаються власними значеннями енергії. Сукупність власних значень Е утворюють енергетичний спектр частинки. Коли U – монотонна функція і 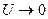на нескінченності, то в області 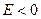власні значення енергії утворюютьдискретний спектр. Отже, з рівняння Шредінгера автоматично випливає квантованість основних параметрів мікросистеми. Знаходження власних значень енергії і власних функцій є задачею квантової механіки.

4⁰. Коли , часове рівняння Шредінгера має рішення:

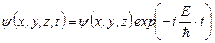(7.8)

Залежність стану частинки від часу t описується періодичною функцією часу з циклічною частотою , яка визначається енергією Е частинки. Ця формула відповідає зв’язку енергії частинки Е з частотою хвилі де Бройля.

Коли частинка знаходиться в енергетичному стані з 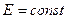, то ймовірність 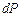знайти її в елементі об’єму не залежить від часу:

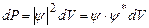
Такий стан частинки називається стаціонарним станом.

Атом, який знаходиться в стаціонарному стані, має постійну енергію і не випромінює електромагнітних хвиль.

Дата добавления: 2014-01-07