Види алгоритмів пошуку: послідовний, бінарний

End

Begin

End

Звернемо увагу на те, що підпрограма-процедура swap рядку (4) використовується в багатьох алгоритмах впорядкування для перестановки елементів місцями. Код цієї процедури наведено нижче:

procedure swap (x,y)

temp ← x

x ← y

y ←temp

Для визначення часової складності алгоритму виконаємо наступні дії. Біля кожного рядку алгоритму зазначимо його вартість (число операцій) і кількість разів, за яку виконується цей рядок. Зауважимо, що рядки усередині циклу виконуються на один раз менше, ніж перевірка, оскільки остання перевірка виводить з циклу. Для кожного j від 1 до i підрахуємо, скільки разів буде виконаний рядок (3), і позначимо це число через kj. Аналогічну дію виконаємо і для рядку (4).

Таблиця 1 – Визначення часової складності алгоритму впорядкування обміном

№	Команда	Вартість	Кількість виконань
(1)	for i←n-1 step -1 until 1 do	с1	п
(2)	for j←1 step 1 until і do	с2	п-1
(3)	if a[j] > a[j+1] then	с3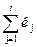
(4)	swap(a[j], a[j+1])	с4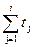

Рядок вартістю с, що повторений m разів, дає внесок cm в загальну кількість операцій. Склавши внески всіх рядків, одержимо вираз, що позначає часову складність алгоритму впорядкування обміном:

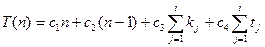
Обчислимо суму кількості виконань для рядку (3).

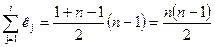
Таким чином, часова складність алгоритму T(n) дорівнює:

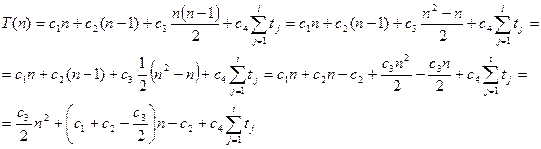
Як бачимо, функція Т(n) – квадратична, тобто має вигляд Т(n)=an²+bn+с, де константи a, b i c визначаються значеннями c₁, … c₄.

Слід зауважити, що час роботи алгоритму залежить не тільки від n, але і від того, який саме масив розмірністю n поданий їй на вхід. Для алгоритму впорядкування обміном найбільш сприятливий випадок, коли послідовність уже впорядкована. Процедура обміну swap у такому разі не буде виконана жодного разу, а часова складність алгоритму T_min(n) дорівнюватиме:

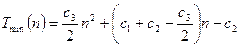
Таким чином, у найбільш сприятливому випадку час T_min(n), необхідний для обробки масиву розміру n, залишається бути квадратичною функцією від n.

Якщо ж масив розташований у зворотному (спадному) порядку, час роботи алгоритму буде максимальним: кожен елемент a[j] прийдеться міняти місцями з елементом a[j+1]. При цьому t_j = j.

Обчислимо суму кількості виконань для рядку (4).

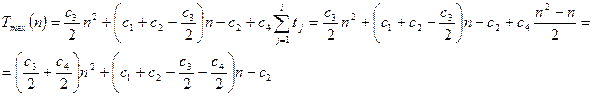Як бачимо, у гіршому випадку час роботи алгоритму T_mах(n) також є квадратичною функцією від n.

Аналіз середнього значення часової складності алгоритму впорядкування обміном T_avg(n) залежить від обраного розподілу ймовірностей, і на практиці реальний розподіл може відрізнятися від передбачуваного, який, зазвичай, вважають рівномірним. Іноді рівномірний розподіл моделюють, використовуючи генератори випадкових чисел. Проте, можна припустити, що в середньому обмін відбувається приблизно у і/2 випадках і його загальна кількість приблизно дорівнює значенню (1+2+..+n)/2≈n²/4. У такому випадку середнє значення часової складності алгоритму впорядкування обміном T_avg(n) можна показати формулою:

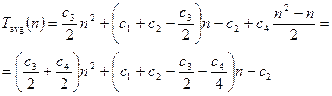
Звичайно, алгоритм впорядкування обміном можна легко модифікувати. Один із шляхів полягає у тому, що можна позбавитися великої кількості непотрібних порівнянь, запам’ятавши чи відбувався обмін на попередньому кроці. Якщо обміну не було, то послідовність вважається впорядкованою, і алгоритм закінчує роботу. Цей процес удосконалення алгоритму можна продовжити, якщо запам’ятовувати не тільки сам факт обміну, але і місце (індекс) останнього обміну. Адже зрозуміло, що всі пари елементів з індексом, меншим від j, вже упорядковані, і наступні перегляди можна закінчувати на цьому індексі.

Проте, всі запропоновані нами вдосконалення жодним чином не впливають на кількість обмінів – вони лише зменшують кількість надлишкових повторних перевірок. Нажаль, обмін двох елементів – більш ресурсоємна операція, ніж порівняння, тому всі наші вдосконалення дають лише незначний ефект.

Таким чином, аналіз алгоритму впорядкування обміном показав, що ніяких переваг, окрім легкозапам’ятовуючої назви, цей алгоритм не має. Проте, саме на прикладі цього алгоритму ми розглянули методику визначення часової складності алгоритмів, яку надалі застосуємо при аналізі інших алгоритмів.

Впорядкування вибором

Ідея методу впорядкування вибором полягає у тому, що на i -му кроці вибирається найменший елемент серед елементів послідовності a[i]..a[n], який міняється місцями з елементом a[i].

У залежності від результату пошуку елемент a[i] або залишається в i- ій позиції або вони міняються місцями і процес повторюється.

Таблиця 2 – Визначення часової складності алгоритму впорядкування вибором

№	Команда	Вартість	Кількість виконань
(1)	for i←1 step1 until n-1 do	с1	n
	begin{for}
(2)	min←a[i]	с2	n-1
(3)	index←i	с3	n-1
(4)	for j←i+1 step 1 until n do	с4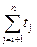
	begin {for}
(5)	if a[j] < min then	с5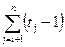
	begin{if}
(6)	min←a[j]	с6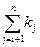
(7)	index←j	с7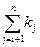
	end{if}
(8)	swap(a[i], a[index])	с8	n-1
	end{for}
	end{for}

Склавши внески всіх рядків, одержимо вираз, що позначає часову складність алгоритму впорядкування вибором:

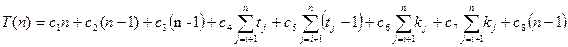
Обчислимо суму кількості виконань оператора повторення рядка (4) і оператора умови, що знаходиться в рядку (5).

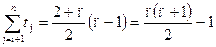
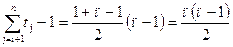
Таким чином, часова складність алгоритму T(n) дорівнює:

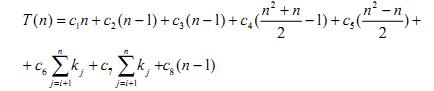
Слід зауважити, що, як і у випадку впорядкування обміном, час роботи алгоритму впорядкування вибором залежить не тільки від n, але і від того, яка саме вихідна послідовність розмірністю n. Обчислення часових складностей Tmax(n) і Tavg(n) алгоритму впорядкування вибором відбувається аналогічним до алгоритму впорядкування обміном чином.

У випадку, коли послідовність уже впорядкована оператори в рядках (6)-(7) виконуватися не будуть. Таким чином, часова складність алгоритму Tmin(n) дорівнюватиме:

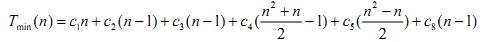
Як бачимо, навіть у найбільш сприятливішому випадку час Tmin(n), необхідний для обробки послідовності, залишається бути квадратичною функцією від n. Слід зазначити, що, незважаючи на відсутність значної різниці в значенні функції Т(n) алгоритму впорядкування вибором у порівнянні з алгоритмом впорядкування обміном, впорядкування вибором є більш придатнішим. Пов’язано це, зокрема, з таким моментом. Кожен з алгоритмів використовує процедуру обміну swap(x,y). В алгоритмі впорядкування обміном ця процедура виконується не менш, ніж n(n-1)/2 разів. Але, оскільки процедура swap(x,y) виконується після оператора умови, то можна очікувати, що кількість обмінів буде дещо меншим за n(n-1)/2. Однак, в алгоритмі впорядкування вибором процедура swap (x,y) знаходиться поза внутрішнім оператором повторення і тому виконується рівно n-1 раз для послідовності розмірністю n. А це значно менше за розглянуту в алгоритмі впорядкування обміном кількість.

Впорядкування вставками

Ідея методу полягає у тому, що розглядаються дії алгоритму на його i-му кроці. При цьому, послідовність розділена на дві частини: впорядковану a[1]...a[i] і неупорядковану a[i+1]...a[n]. На кожному наступному, (i+1)-му кроці алгоритму береться a[i+1] елемент і вставляється на потрібне місце в упорядковану частину послідовності.

Пошук потрібного місця для чергового елемента вхідної послідовності здійснюється шляхом послідовних порівнянь з елементом, що знаходиться перед ним. У залежності від результату порівняння елемент або залишається на поточному місці (вставка закінчена), або вони міняються місцями і процес повторюється.

Таким чином, у процесі вставки елемент x якби „просівається” до початку масиву. При цьому зупинка відбувається у випадку коли:

• знайдено елемент, менший від x або

• досягнуто початок послідовності.

Біля кожного рядку процедури зазначимо його вартість (число операцій) і кількість разів, за яку виконується цей рядок. Для кожного i від 2 до n підрахуємо, скільки разів буде виконаний рядок (4), і позначимо це число через t_i.

Таблиця 3 – Визначення часової складності алгоритму впорядкування вставками

№	Команда	Вартість	Кількість виконань
(1)	for i←2 step1 until n do	с1	n
	begin{for}
(2)	key←A[i]	с2	n-1
(3)	j←i-1	с3	n-1
(4)	while (j>0) and (a[j]>key) do	с4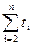
	begin{while}
(5)	a[j+1]←a[j]	с5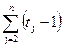
(6)	j←j-1	с6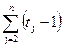
	end{while}
(7)	a[j+1]←key	с7	n-1
	end{for}

Склавши внески всіх рядків, одержимо вираз, що позначає часову складність алгоритму впорядкування вставками:

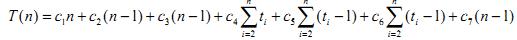
Як і у випадку аналізу алгоритму обміном, зауважити, що час роботи процедури залежить не тільки від n, але і від того, який саме масив розмірністю n поданий їй на вхід.

Якщо вихідна послідовність вже упорядкована у зворотному (спадному) порядку, час часова складність роботи алгоритму Тmax(n) буде максимальною: кожен елемент a[j] прийдеться порівнювати з усіма елементами a[j-1].. a[1].

При цьому t_і = і. Обчислимо суми

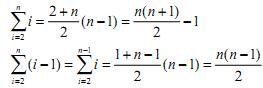
Як бачимо, у найгіршому випадку часова складність роботи алгоритму Тmax(n) буде дорівнює

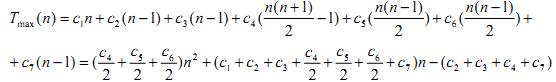
Функція Тmax(n) - квадратична, тобто має вигляд багаточлена (полінома) Тmax(n)=an²+bn+с, де константи a, b i c визначаються значеннями c₁, … c₇.

Середнє значення часової складності роботи алгоритму Тavg(n) буде доволі близьким до Тmax(n), адже в середньому біля половини елементів послідовності a[1]..a[j-1] більше за a[j]. Це означає, що t_i в середньому можна вважати рівним і /2, отже і функція часової складності роботи алгоритму Тavg(n) буде квадратичною:

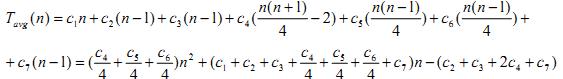
Цікаво, що у найбільш сприятливішому випадку (послідовність впорядкована), рядок (4) завершується після першої ж перевірки, так що всі t_і рівні 1, і часова складність Тmin(n) дорівнює

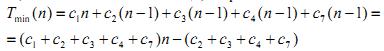
Таким чином, у найбільш сприятливішому випадку час Тmin(n), необхідний для впорядкування послідовності розмірністю n, є лінійною функцією від n, тобто має вигляд Тmin(n)=an+b для деяких констант а і b (ці константи знову визначаються обраними значеннями с₁,...,с₇).

Наведений приклад показує, що час роботи у найгіршому та найбільш сприятливішому випадках може значно відрізнятися.

Послідовний пошук – алгоритм, що по черзі порівнюють елементи заданого списку з ключем до тих пір, доки не знайдуть елемент з вказаним значенням ключа (вдалий пошук) або весь список буде перевірений, але необхідний елемент не знайдений (невдалий пошук). Частіше застосовується простий додатковий прийом: якщо додати ключ вкінець списку, то пошук обов’язково буде вдалим, тобто, можна прибрати перевірку завершення списку в кожній ітерації алгоритму. Розглянемо псевдокод такої поліпшеної версії, вважаємо, що вхідні данні мають вид масиву.

Алгоритм SequentialSearch (А [0.. п], К)

// Вхідні дані: Масив А з п елементів та ключ пошуку К

// Вихідні дані: Позиція першого елементу масиву

// А[0.. п — 1], значення якого співпадає с К; якщо елемент не знайден, повертає начення –1

А[ п ] 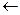К

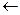і 0

Дата добавления: 2014-01-07