Расчет зубьев цилиндрических прямозубых колес на контактную прочность

Расчет сводится к удовлетворению условия, чтобы рабочие контактные напряжения не превышали допускаемые. Расчет ведут для зацепления в полюсе, т.к. выкрашивание начинается у полюсной линии в зоне однопарного зацепления. В качестве исходной принимают формулу Герца для определения σ_Н (касательных напряжений) при сжатии цилиндров, соприкасающихся вдоль образующих.

Е_пр – приведенный модуль упругости материалов сопряженных зубчатых колес; , где Е₁ и Е₂ – модули упругости материалов шестерни и колеса. Если Е₁ = Е₂, то Е_пр = Е = 2,15·10⁵.

μ – коэффициент Пуассона (поперечное сжатие); для стали μ 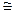0,3;

q – удельная нагрузка, действующая нормально к профилю зуба

,

где F_n – сила нормального взаимоотношения между зубьями; l _Σ – суммарная длина контактных линий; l _Σ = b_w; К_ε·ε_α = 1.

Определим ρ_пр – приведенный радиус кривизны профилей зубьев в зоне контакта. Он находится из зависимости:

.

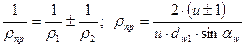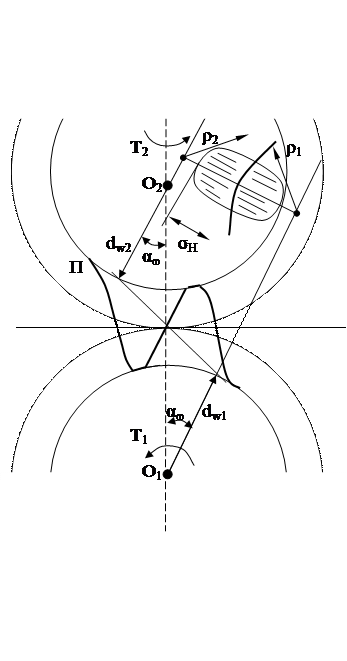
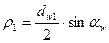- радиус кривизны зуба шестерни;

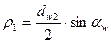- радиус кривизны зуба колеса.

Приведенная кривизна:

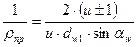
Подставляя полученные значения в формулу Герца, получим:

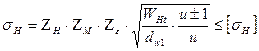(4)

(4) – основная формула для расчетов цилиндрических прямозубых колес на контактную прочность.

В формуле обозначено:

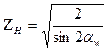· - коэффициент, учитывающий форму сопряженных поверхностей зубьев; при α_w = 20⁰ Z_Н = 1,77

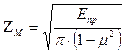· - коэффициент, характеризующий механические свойства материалов сопряженных зубчатых колес; Z_М = 275 – для стальных колес

· Z_ε – коэффициент, характеризующий влияние коэффициента торцевого перекрытия ε_α или суммарную длину контактных линий l _Σ; l _Σ колеблется от b_w - в зоне контактного зацепления до 2 b_w – в зоне двухпарного зацепления. Расчет ведут по некоторой эффективной длине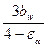

При отсутствии требований повышенной точности расчетов можно принимать: 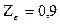- соответствует ε_α = 1,6

· и – передаточное число рассчитываемой пары.

Величина расчетных контактных напряжений одинакова для шестерни и колеса. Расчет ведут по тому элементу, для которого меньше [σ_H]. Чаще это колесо, а не шестерня.

Формулу (4) применяют при проверочных расчетах. При проектных расчетах определяют а_w или d_w1 (можно и d_w2) по заданным Т₁, Т₂ и и. С этой целью формулу (4) решают относительно а_w или d_w1. При этом в формуле оставляют только те из неизвестных параметров, которые можно оценить или выбрать на основе накопленного опыта. Другие неизвестные параметры включают в обобщенный коэффициент, которому дают приближенную оценку. Обозначим 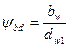и найдем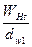

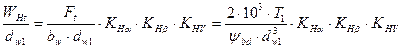
Подставляя это значение в (4), получим:

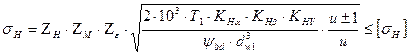
Решая относительно d_w1, получим:

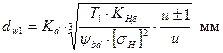(5)

(5) – основная формула для проведения проектных расчетов. Здесь за К_d обозначено: - вспомогательный коэффициент; К_d = 770 – для стальных колес;

Т₁ – критический момент на валу шестерни рассчитанной пары, (Н·м);

и – передаточное число пары.

Решая (4) относительно а_w, заменим:

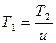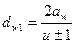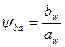; ; - коэффициент ширины колес; .

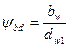После преобразования формулы (4) получим:

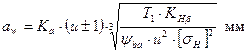(6)

(6) – основная формула для расчета межосевого расстояния, где

- вспомогательный коэффициент; К_а = 495 – для прямозубых передач. Формулы (5) и (6) равноправны. При расчете по этим формулам нужно задаваться значениями ψ_ba и ψ_bd. Их выбирают в зависимости от расположения колес относительно опор, твердости зубьев и вида передачи. Имеются таблицы и рекомендации. Если по условию проектного задания основные параметры редуктора (механизма) должны соответствовать ГОСТ (это требование обычно ставится при проектировании редукторов для серийного выпуска), то значение а_w должно быть определено по ГОСТ. В этом случае предпочтительнее формула (6).

· ψ_ba = 0,3…0,4 для размеров в основном диапазоне редукторов;

· ψ_ba = 0,15…0,2 для КПП;

· ψ_ba = 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25 – стандартный ряд значений ψ_ba.

Для многоступенчатых редукторов, у которых нагрузка повышается от ступени к ступени, каждой последующей ступени значения ψ_ba и ψ_bd принимают больше, чем в предыдущей. Это способствует хорошему соотношению размеров колес по ступеням. Увеличение ширины колес или ψ_ba или ψ_bd позволяет уменьшить габариты и массу передачи, но требует повышение точности изготовления и жесткости конструкции. Ширину колес ограничивают, т.к. с увеличением ширины колес возрастает К_Hβ и ликвидируются преимущества увеличения ширины. Коэффициенты ψ_ba и ψ_bd находят: 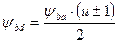. Проще задаваться значением ψ_ba.

ψ_bd характеризует шестерню.

Если одно или оба колеса выполнены не из стали, то в формулах (5) и (6) численные коэффициенты нужно умножить на .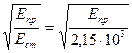

Если зубчатая передача выполнена с угловым смещением, то те же коэффициенты умножаются на 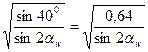, где α_w – угол зацепления пары со смещением.

Контактная прочность зубчатых колес (формулы 4, 5, 6) зависит от радиусов кривизны профилей зубьев, которые выражаются через d_w и a_w, ширины колес b_w и от передаточного числа и, но совсем не зависит от модуля.

Модуль передачи может быть сколь угодно малым, лишь бы выполнялось условие:

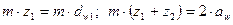
Минимально допустимую величину модуля можно определить:

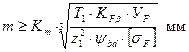- зависит от расчета на изгиб.

Но часто получаются зубья с очень мелким модулем, применения ограничено. Лучше определить модуль из условия равнопрочности зубьев на изгиб и контактную прочность, выразив:

.

После преобразования формулы (3) получим:

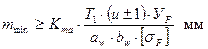, (7)

где К_ma = 1400 для прямозубых передач.

Т₁ – в Н·м; У_F – в мм; a_w – в мм; b_w – в мм; [σ_F] – МПа.

С другой стороны величина модуля должна быть проверена по условию:

,

где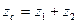

Модуль выбирается больший из выражения (7).

В передачах большинства редукторов модуль выбирают:

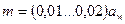- для улучшаемых и нормализованных колес;

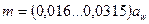- для закаленных колес.

Большее значение соответствует работе с неизбежным износом, кратковременным режимом работы, значительными перегрузками и средними скоростями. Меньшее значение – продолжительным режимом работы, малыми перегрузками и большими скоростями.

Модуль зубчатых колес нужно выбирать минимальным, т.к. с его увеличением растут наружные диаметры заготовок и вес, трудоемкость обработки и потери на трение. С другой стороны 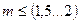мм – для силовых передач принимать не рекомендуют из-за возможности большого понижения несущей способности в результате износа, повышенного влияния неоднородности материалов, опасности разрушения при перегрузках.

Дата добавления: 2014-01-06