Определение расчетных нагрузок при расчете зубчатых передач

К₁ – коэффициент нагрузки при расчете на изгиб и контактную прочность.

Y₁ – специфический коэффициент при расчете на изгиб.

Z₁–специфический коэффициент при расчете на контактную прочность.

F₁ – индекс, обозначающий расчет на изгиб.

H₁ – индекс, обозначающий расчет на контактную прочность.

L – расчет на малоцикловую выносливость.

М – расчет по max напряжениям.

Р – допускаемые напряжения.

1 – индекс, относящийся к шестерни или к валу шестерни.

2 – к колесу или к валу колеса.

σ_HPM1 – допускаемое контактное напряжение для шестерни

σ_FPM1 – допускаемое напряжение изгиба для шестерни

[σ_H1]_max; [σ_F1]_max

Расчетная нагрузка на зубчатые колеса складывается из:

a) Полезной или номинальной нагрузки, в предположении, что она распределяется по длине зубьев равномерно

b) Внешней динамической нагрузки

c) Дополнительной нагрузки на опасном участке длины зубьев из-за упругих перекосов валов и начальных погрешностей изготовления, т.е. из концентрации нагрузки

d) Дополнительной динамической внутренней нагрузки, связанной с погрешностями изготовления и др. факторами.

Расчетная нагрузка:

,

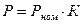где К – коэффициент нагрузки; Р_ном – номинальная нагрузка.

,

где К_А – коэффициент внешней динамичности нагрузки; К_α – коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых колес с 7-ой степенью точности К_α = 1; К_β – коэффициент концентрации нагрузки (коэффициент неравномерности распределения нагрузки по ширине колеса); К_V – коэффициент внутренней динамичности нагрузки.

Нагрузка по длине зуба или ширине колеса распределяется равномерно только при идеально точном изготовлении передачи и при абсолютно жестких валах и опорах. В действительности из-за упругих деформаций валов, упругих смещений, износа подшипников и погрешностей изготовления зубчатые колеса перекашиваются друг относительно друга. Поясним это явление на примере, учитывающем только прогиб валов.

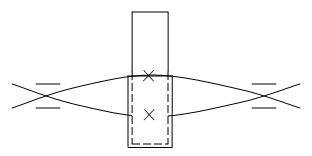
Самое благоприятное расположение валов

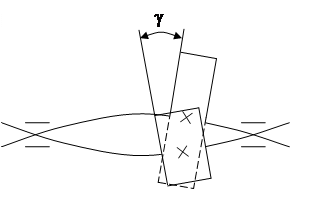
Несимметричное расположение валов относительно опор

Передачи по прирабатываемости делят на:

a) Прирабатывающиеся (если НВ 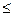350 хотя бы одного из колес, а окружная скорость < 15 м/с)

b) Неприрабатывающиеся (если оба колеса НВ 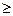350; υ > 15 м/с).

Для прирабатывающихся колес различают начальный коэффициент концентрации нагрузки К⁰_β и К_β (после проработки).

Расчет К_β связан с определением угла γ. Нужно учитывать не только деформации валов, опор и самих колес, но и ошибки монтажа и приработку зубьев. Это сложно. Для определения К_β используют графики. Составленные на основе расчета и практики эксплуатации.

Для уменьшения К_β следует:

a) Повысить точность изготовления передач

b) Повысить жесткость валов и опор

c) Выбирать более благоприятное расположение колес относительно опор

d) Выполнять зубья бочкообразными с небольшой конусностью или в виде конусной бочки.

Неизбежные ошибки в изготовлении и сборке зубчатых колес, а также деформации зубьев под нагрузкой приводят к тому, что при равномерном вращении шестерни колесо вращается неравномерно, т.е:

.

Это приводит к работе передачи с шумом и вибрациям и к динамическим нагрузкам.

Величина дополнительных динамических нагрузок зависит от величины ошибки шага, окружной скорости, присоединенных масс, упругости зубьев и др. деталей передач.

Расчет К_V не менее сложен чем К_β. Чаще принимают:

,

где ν – динамическая добавка;

W_V – удельная окружная динамическая сила;

,

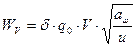где δ – коэффициент, учитывающий проявление погрешностей зацепления на динамическую нагрузку; q₀ – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса; V – окружная скорость; a_ω – межосевое расстояние; u – передаточное число.

,

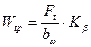где W_tp – удельная расчетная окружная сила; b_ω – расчетная ширина колес; F_t – окружная сила.

Для уменьшения К_V следует:

· Повышать точность изготовления передачи и монтажа

· Делать зубья шестерни и колеса равнопрочными по напряжениям изгиба

· Применять модификацию (плантирование зубьев) – для быстроходных передач.

Влияние дополнительных нагрузок различно на прочность зубьев при изгибе и контактным напряжениям, поэтому различают:

- при расчете на изгиб

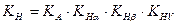- на контактную прочность.

Дата добавления: 2014-01-06