Шкали найменувань

Припустимо, що число відмінних станів (математичний термін – число класів еквівалентності) скінчене. Кожному класу еквівалентності поставимо у відповідність позначення, відмінне від позначень інших класів. Тепер вимірювання буде полягати в тому, що, виконуючи експеримент над об’єктом, визначити приналежність результату до того чи іншого класу еквівалентності та записати це за допомогою символу, який позначає даний клас. Таке вимірювання називається вимірюванням у шкалі найменувань (іноді цю шкалу називають також номінальною або класифікаційною); вказана множина і утворює шкалу.

Істотно використовувати шкалу найменувань у тих випадках, коли класифікуються дискретні за своєю природою явища (наприклад, різні об’єкти). Для позначення класів можуть бути використаними як слова природної мови (наприклад, географічні назви, власні імена людей тощо), довільні символи (герби та прапори держав, емблеми родів війська і т. д.), номера (реєстраційні номера авто, офіційних документів, номера на майках спортсменів), так і їх різні комбінації (наприклад, поштові адреси, екслібриси власних бібліотек та інше). Усі ці позначення еквівалентні простій нумерації (усі ми маємо ідентифікаційний код).

Оскільки позначення, що присвоюється класам, у принципі довільне (хоча після присвоєння однозначне), цю свободу вибору можна використати для зручності. Так, при великому та/або нефіксованому числі класів їх конкретизація спрощується та полегшується, якщо позначення вводяться ієрархічно. Прикладом можуть служити поштові адреси (країна, область, місто) – населений пункт – вулиця – будинок – квартира.

Необхідність класифікації виникає і у тих випадках, коли стани, що класифікуються, створюють неперервну множину. Задача зводиться до попередньої, якщо всю множину розбити на скінчене число підмножин, штучно створюючи тим самим класи еквівалентності. Тепер приналежність стану до якогось класу знову можна реєструвати у шкалі найменувань. Однак умовність введення класів (не їх шкальних позначень, а самих класів) рано чи пізно проявиться на практиці. Наприклад, виникають труднощі точного перекладу з однієї мови на іншу при описі кольорових відтінків: в англійській мові голубий, лазуровий та синій кольори не відрізняються; не виключено, що англійці інакше бачать світ (наприклад, в одному англійському тлумачному словнику слово “синій” пояснюється як “колір чистого неба, деревного диму, знятого молока, свинцю”, а у другому – як “колір неба або моря, а також речей більш блідих або темніших, як дим, віддалені пагорби, місячне світло, синяк”).

Назви хвороб також створюють шкалу найменувань. Психіатр, ставлячи хворому діагноз “шизофренія”, “параноя”, “маніакальна депресія” або “психоневроз”, використовує номінальну шкалу; і все ж іноді лікарі не дарма згадують, що “треба лікувати хворого, а не хворобу”: назва хвороби лише позначає клас, усередині якого насправді існують відмінності, тому що еквівалентність усередині класу носить умовний характер. Треба твердо пам’ятати, що позначення класів – це тільки символи, навіть якщо для цього використані номера. Номера лише зовні виглядають як числа, насправді вони числами не являються. Якщо в одного спортсмена на формі № 4, а у другого – № 8, то ніяких інших висновків, окрім того, що це різні учасники змагань, робити не можна. Не можна сказати, що другий “удвічі кращий”. З номерами не можна поводитися як з числами, виключно визначення їх рівності або нерівності: тільки ці відношення визначені між елементами номінальної шкали.

Тому при обробленні експериментальних даних, зафіксованих в номінальній шкалі, безпосередньо із самими даними можна виконувати тільки операцію перевірки їх збігу або не збігу. Зобразимо цю операцію за допомогою символу Кронекера: δ _{ij =} { 1: x _i = x _j; 0: x _i ≠ x _j}, де x _i та x _j – записи різних вимірів.

З результатами цієї операції можна виконувати більш складні перетворення: рахувати кількість збігів (наприклад, число спостережень k –го класу дорівнює n _k = 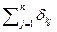, n – загальне число спостережень), обчислювати відносні частоти класів (наприклад, частота k –го класу є p _k = n _k/ n), порівнювати ці частоти між собою (знаходячи, наприклад моду – номер найбільш зустрічаємого класу k _max = arg p _k), виконувати різні статистичні процедури, суворо слідкуючи, однак, щоби у цих процедурах з вихідними даними не виконувалося нічого, окрім операції перевірки їх на спів падання (наприклад, можна використати χ ²–тест, інші тести на відносні частоти, коефіцієнт погодженості тощо).

Порядкові шкали

У випадках, коли спостережувана (вимірювана) ознака стану має природу, що не тільки дозволяє ототожнювати стани з одним із класів еквівалентності, але й дає можливість у деякому відношенні порівнювати різні класи, то для вимірювань можна вибрати більш сильну шкалу, ніж номінальна. Якщо ж не скористатися цим, то ми відмовимося від частки корисної інформації. Однак посилення вимірювальної шкали залежить від того, які саме відношення між класами дійсно існують.

Наступною по силі за номінальною шкалою є порядкова шкала (використовується також назва рангова шкала). Цей клас шкал з’являється, якщо окрім аксіом тотожності 1⁰ – 3⁰ класи задовольняють наступним аксіомам впорядкованості:

4⁰. Якщо А > B, то B < A.

5⁰. Якщо А > B, та B > C, то A > C.

Позначивши такі класи символами та встановивши між цими символами відношення порядку, отримаємо шкалу простого порядку. Прикладами застосування такої шкали являються нумерація у черзі, військові звання, призові місця у конкурсі.

Іноді виявляється, що не кожну пару класів можна впорядкувати по перевазі: деякі пари вважаються рівними. У такому випадку аксіоми 4⁰ та 5⁰ видозмінюються:

4’. Або А ≤ B, або А ≥ B.

5’. Якщо А ≥ B та B ≥ C, то A ≥ C.

Шкала, що відповідає аксіомам 4⁰ та 5⁰ називається шкалою слабкого порядку. Прикладом такої шкали служить упорядкування за ступенем спорідненості з конкретною особою (мати = батько > син = дочка, дядько = тітка < брат = сестра і т. п.).

Інша ситуація виникає, коли є пари класів, не порівняних між собою, тобто ані А ≤ B, ані В ≤ А (це відрізняється від умови слабкого порядку, коли одночасно А ≥ B та В ≥ А, тобто А = В). У такому випадку кажуть про шкалу часткового порядку. Шкали часткового порядку виникають у соціологічних дослідженнях суб’єктивних переваг. Наприклад, при вивченні покупного попиту суб’єкт часто не у змозі оцінити, який саме з двох різних товарів йому більше подобається (наприклад, клітчаті шкарпетки чи фруктові консерви, велосипед чи магнітофон тощо).

Характерною особливістю порядкових) шкал є те, що відношення порядку нічого не каже про дистанцію між класами, що порівнюються. Тому порядкові експериментальні дані, навіть якщо вони зображені цифрами, не можна розглядати як числа, над ними не можна виконувати дії, що приводять до отримання різних результатів при перетворенні шкали, не порушуючи порядку. Наприклад, не можна обчислювати вибіркове середнє порядкових вимірів, тобто 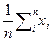, тому що перехід до монотонно перетвореної шкали x ` = f ( x ) при усередненні дасть 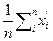≠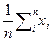. Однак допустима операція, що дозволяє встановити, котре з двох спостережень, x _i або x _j, переважає, хоча формально цю операцію можна виразити через різницю x _i - x _j. Введемо індикатор додатних чисел – функцію C ( t ) = {1: t ≥ 0; 0: t < 0 }. Тоді, якщо x _i ≥ x _j і ми ввели цифрову шкалу порядку, то C ( x _i - x _j) = 1, а C ( x _j – x _i) = 0, що і дозволяє встановити перевагу x _i перед x _j. Число R i = 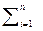C ( x _i - x _j), де n – число порівнюваних об’єктів (1 ≤ R _i ≤ n), називається рангом i –го об’єкта. (Звідси походить друга назва порядкових шкал – рангові). Якщо має місце слабкий порядок, то частина спостережень співпадає і всі члени отримують однаковий (старший для них) ранг.

Таким чином, при вимірах у порядкових (у суворому смислі) шкалах оброблення даних повинне основуватися тільки на допустимих для цих шкал операціях – обчисленні δ _ij та R i. З цими числами можна “працювати” далі вже довільним чином: окрім знаходження частот та мод (як і для порядкових шкал), дозволяється можливість визначити вибіркову медіану (тобто спостереження з рангом R i, найближче до числа n / 2); можна визначити коефіцієнти рангової кореляції між двома серіями порядкових спостережень (r _s Спірмена, τ Кендала); будувати за допомогою отриманих величин інші статистичні процедури.

Суть зауваження “у суворому смислі” полягає у тому, що порядкові у суворому смислі шкали визначаються тільки для заданого набору порівняних об’єктів, у цих шкал немає загальноприйнятого, а тим більше абсолютного, стандарту. Тому при деяких умовах правомірне висловлювання “перший у світі, другий в Європі” – просто чемпіон світу зайняв друге місце на європейських змаганнях.

6. Модифіковані порядкові шкали

Мабуть, досвід роботи із сильними числовими шкалами та бажанням зменшити відносність порядкових шкал, надати їм хоча б зовнішню незалежність від вимірюваних величин спонукає дослідників до різних модифікацій, що придають порядковим шкалам (так лише здається) посилення. Друга важлива причина спроб посилення шкали полягає у тому, що багато вимірюваних у порядкових (принципово дискретних) шкалах величини мають дійсний або мислимий неперервний характер: сила вітру або землетрусу, твердість речовини, глибина та міцність знань, володіння навичками тощо. Сама можливість введення між довільними двома значеннями третього сприяє спробам посилити шкалу.

Все це разом узяте привело до появи та практичного використання порядкових шкал, але не у такому “суворому смислі”, як згадувані. При цьому іноді з отриманими даними починають оперувати як із числами, навіть якщо зроблена модифікація не виводить шкалу із класу порядкових. Ось деякі із відомих модифікацій.

Шкала твердості по Моосу. Із двох мінералів твердіший той, що залишає на другому подряпини або вм’ятини при достатньо сильному стисканні. Відношення “А твердіше В” – типове відношення порядку. У 1811 р. німецький мінералог Ф. Моос запропонував посилити стандартну шкалу твердості, постулюючи тільки десять градацій. За еталони прийняті наступні мінерали із зростаючою твердістю: 1 – тальк, 2 – гіпс, 3 – кальцій, 4 – флюорит, 5 – апатит, 6 – ортоклаз, 7 – кварц, 8 – топаз, 9 – корунд, 10 – алмаз. Шкала Мопса встановлює штучний слабкий порядок, так як проміжних одиниць градацій твердості ця шкала не має. Градації твердості все рівно не носять числового характеру: не можна казати ні що алмаз у двічі твердіше апатиту, ні що різниця у твердості флюориту та гіпсу така ж, як у корунду та кварцу; виміри твердості методом подряпування не дають підстав для виправдання таких тверджень.

Шкала сили вітру по Бофорту. У 1806 р. англійський гідрограф та картограф адмірал Ф. Бофорт запропонував бальну шкалу сили вітру, визначаючи її по характеру хвилювання моря: 0 – штиль, 4 – помірний вітер, 6 – сильний вітер, 10 – шторм (буря), 12 – ураган. Окрім штиля, градації сили вітру мають умовний, якісний характер.

Шкала магнітуд землетрусів по Ріхтеру. У 1935 р. американський сейсмолог Ч. Ріхтер запропонував 12-бальну шкалу для оцінки енергії сейсмічних хвиль у залежності від наслідків проходження їх по даній території. Потім він розвинув метод оцінки сили землетрусу в епіцентрі по його магнітуді на поверхні землі та глибині.

Бальні шкали оцінки знань учнів. Слухаючи відповіді учнів або порівнюючи їх письмові роботи, досвідчений викладач може знайти різницю між ними і встановити, чиї відповіді краще. Це типове відношення порядку.

Потреба суспільства в офіційному визначенні ступеня кваліфікованості учнів незалежно від того, де, коли та як вони отримують освіту, сприяла введенню загальноприйнятих шкал для оцінювання знань учнів у вигляді балів (такі шкали введені всюди). Всі відчувають, у тому числі й на власному досвіді, неточність, наближеність цієї шкали. Одна із спроб “покращити” шкалу балів полягає у збільшенні числа градацій. У школах прийнята 12-бальна, у вузах – 2-бальна (для заліків) та 4-бальна (для іспитів) система оцінок, у деяких європейських країнах 10-бальна, а в англомовних країнах – 100-бальна система. Це не рятує положення, і викладачі неофіційно (“для себе”) вводять додаткові градації – приєднують до балів плюси, мінуси, точки. Все це відбувається тому, що не існує ні абсолютного стандарту, подібно до еталонів твердості або висоти хвиль, і знання можуть оцінюватися лише у порядковій шкалі. Тим не менше мало хто (не тільки учні, а й викладачі) розуміють, що бальна шкала належить до класу порядкових. Справа доходить до того, що навіть в офіційних випадках, що впливають на долі людей, враховують середньоарифметичний бал – величину, що не має смислу у порядковій шкалі! Деякий відтінок об’єктивності бальній шкалі намагаються придати директивним визначенням того, яким вимогам потрібен задовольняти учень, щоби мати право на той чи інший бал, тобто ввести незалежні стандарти. Однак викладачі неминуче по-різному розуміють та виконують інструкції, і оцінки все рівно стають відносними. Відомо, що рівень знань відмінників різних шкіл або вузів помітно різняться. Саме тому у відповідальних випадках влаштовують не конкурси документів, а конкурси самих претендентів, тобто вертаються до порядкового вимірювання, безпосереднього порівняння володарів знання.

7. Шкали інтервалів

Якщо впорядкування об’єктів можна виконати настільки точно, що відомі відстані між довільними двома з них, то вимір виявиться помітно сильнішим, ніж у шкалі порядку. Істотно виражати всі відстані в одиницях, хоча й довільних, проте однакових по всій довжині шкали. Це означає, що об’єктивно рівні інтервали вимірюються однаковими по довжині відрізками шкали, де б вони не розміщалися. Наслідком такої рівномірності шкал цього класу являється незалежність відношення двох інтервалів від того, в котрій із цих шкал ці інтервали виміряні (тобто яка одиниця довжини інтервалу та яке значення прийняте за початок підрахунку). Дійсно, якщо два інтервали в одній шкалі виражаються числами ∆ ₁ х та ∆ ₂ х, а при іншому виборі нуля і одиниці ∆ ₁ у та ∆ ₂ у, то, оскільки це об’єктивно ті ж самі інтервали, маємо ∆ ₁ х / ∆ ₂ х = ∆ ₁ у / ∆ ₂ у, звідки випливає, що введені шкали можуть мати довільні початок підрахунку та одиниці довжини, а зв’язок між показаннями у таких шкалах є лінійним: у = ах + b, a > 0, -∞ < b < ∞. Це співвідношення можна виразити словами: ”шкала інтервалів єдина з точністю до лінійних перетворень”

Прикладами величин, котрі по фізичній природі або не мають абсолютного нуля, або допускають свободу вибору в установленні початку розрахунку і тому вимірюються в інтервальних шкалах, являються температура, час, висота місцевості.

Початок літочислення у християн установлене від Різдва Христова, а у мусульман – на 622 роки пізніше – від переїзду Мохамеда (Магомета) у Медину; одиниці літочислення прив’язані до відносних переміщень Сонця та Місяця, проте в астрономії існує цілих шість різних визначень року. Висоту прийнято рахувати від рівня океану, але це призвело до того, що більша частина території Голландії та акваторії Каспійського моря має... від’ємну висоту, бо розташовані нижче рівня океану.

Назва “шкала інтервалів” підкреслює, що у цій шкалі тільки інтервали мають смисл справжніх чисел і тільки над інтервалами слід виконувати арифметичні операції: якщо виконати арифметичні операції над самими підрахунками по шкалі, забувши про їх відносність, та є ризик отримати безглузді результати. Наприклад, якщо сказати, що температура води підвищилася у двічі при її нагріві від 9 до 18⁰ по шкалі Цельсія, то для тих, хто користується шкалою Фаренгейта, це буде звучати досить дивно, тому що у цій шкалі температура води у тому ж досліді зміниться від 37 до 42⁰.

Подібно до того як визначення значення символу Кронекера є єдиною допустимою операцією в номінальній шкалі, а обчислення рангу спостереження – у порядковій шкалі, в інтервальній шкалі єдиною новою допустимою операцією над спостереженнями є визначення інтервалу між ними. Над інтервалами ж можна виконувати довільні арифметичні операції, а разом з ними – використовувати підходящі способи статистичного або іншого оброблення даних.

8. Шкали відношень

Нехай величини, що спостерігаються, задовольняють не тільки аксіомам 4⁰ та 5⁰, але й аксіомам адитивності:

6⁰. Якщо A = P та B > 0, то A + B > P.

7⁰. A + B = B + A.

8⁰. Якщо A = P та B = Q, то A + B = P + Q.

9⁰. (A + B ) + C = A + ( B + C ).

Це суттєве підсилення шкали: виміри у такій шкалі являється “повноправними” числами, з ними можна виконувати довільні арифметичні операції, так як віднімання, множення та ділення – лише часткові випадки додавання. Введена таким чином шкала називається шкалою відношень. Цей клас шкал володіє наступною особливістю: відношення двох значень вимірюваної величини не залежать від того, у котрій з таких шкал зроблені виміри: х ₁/ х ₂ = у ₁/ у ₂. Цій вимозі задовольняє відношення виду у = ах ( а ≠ 0 ). Таким чином, величини, що вимірюються у шкалі відношень, мають істотний, абсолютний нуль, хоча залишається свобода у виборі одиниць.

Прикладами величин, природа котрих відповідає шкалі відношень, являються довжина, вага, електричний опір, гроші.

9. Шкали різниць

До числа шкал, єдиних з точністю до лінійних перетворень, відноситься шкала інтервалів (у = ах + b, a > 0 та b довільні) та шкала відношень (y = ах, a > 0 - перетворення розтягування). Розглянемо особливості шкал, інваріантних до зсуву: y = х + b.

Повторно застосовуючи зсув до y (z = y + b = z + 2 b ), далі до z і т.д., виявляємо, що в такій шкалі значення не змінюється при довільному числі зсувів: y = x + nb, n = 0,1,2,…Постійна b являється характерним параметром шкали і називається її періодом. Отриману шкалу називають шкалою різниць (іноді її називають циклічною або періодичною). У таких шкалах вимірюється напрям із однієї точки (шкала компасу, роза вітрів), час доби (циферблат годинника), фаза коливань (у градусах чи у радіанах).

Циклічні шкали являються частковим випадком інтервальних шкал. Однак угода про хоча і довільний, проте єдиний початок підрахунку шкали дозволяє використовувати покази у цій шкалі як числа, застосовувати до них арифметичні дії (до тих пір, поки хто-небудь не забуде про умовність нуля, наприклад при переході на літній час або навпаки).

Дата добавления: 2014-01-07