Лекція 8. В будь-якому випадку при перевірці надійності повинні залучатись великі репрезентативні групи досліджуваних від 200 осіб і вище

В будь-якому випадку при перевірці надійності повинні залучатись великі репрезентативні групи досліджуваних від 200 осіб і вище

Тема: Пошук у ширину та пошук у глибину

План:

1. Пошук у ширину.

2. Пошук у глибину.

3. Пошук у ширину.

Раніше ми вже розглядали різноманітні пошукові алгорит-ми: пошук заданої інформації в одновимірному масиві, в ме-режі, у рядку. Під час дослідження задач, що пов'язані з оброб-кою інформації, яку можна представити у вигляді графів, та-кож постає питання пошуку. У першу чергу - це пошук шляху від однієї заданої вершини до іншої.

Існує два підходи до здійснення такого пошуку. Розглянемо перший із них - пошук у ширину.

Як відомо, одним із найпоширеніших способів представлен-ня графа є матриця суміжності. Саме на перегляді цієї матриці і базується метод пошуку в ширину.

Для зручнішого пояснення цього методу розглянемо конкрет-ний приклад графа, зображеного на малюнку 1, а та відповідній йому матриці суміжності (мал. 21, б). Нехай також відомо, що необхідно визначити існування у даному графі шляху від вер-шини 1 до вершини 7.

№

а) б)

Мал.1

Почнемо пошук шуканої вершини 7 із заданої вершини 1 і зафіксуємо для себе цю інформацію, будуючи дерево пошуку, в якому на першому кроці нашого пошукового алгоритму є лише одна вершина 1 (мал. 22, а) та послідовність вершин, які перегля-даються (мал. 22, б). Встановимо покажчики перегляду вершин у послідовності так: верхній вказуватиме на номер вершини, з якої ми дивимося, а нижній - на номер останньої «видимої» вершини. Відповідно на першому кроці такою вершиною є єдина вершина 1.

І ще одна інформація, яка може бути нам надалі корисною. Якщо забігти наперед і розглянути заданий граф (мал. 21, а), то можна помітити, що вершину з номером 1 знову побачимо, коли перейдемо до перегляду вершин 2, 3 та 4. Але повертатися у неї немає сенсу, оскільки при цьому ми «зациклимося» і бу-демо крутитися на одному і тому самому місці. Тому варто за-пам'ятовувати номери вершин, у яких ми вже побували, для того, щоб виключити їх надалі з перегляду. Яким чином мож-на реалізувати такий захист? Можна запропонувати два спосо-би: перший - проглядати послідовність переглянутих вершин (мал. 22, б), другий - використати множину для їх фіксації (мал. 2, в). Який з них ефективніший? Якщо кількість вер­шин невелика, то раціональніше скористатися множиною, як-що ж вона більша за 256 - то переглядом послідовності. Але у цьому разі інформацію про заданий граф необхідно представля-ти у вигляді списку суміжних вершин.

Мал.2

Продовжимо пошук вершини 7. З малюнка 21, а видно, що з вершини 1 ми бачимо вершини 2, 3 і 4. Ту саму інформацію ми можемо отримати і з таблиці суміжності (мал. 21, б), пере­глянувши рядок, що відповідає номеру вершини, з якої ми дивимося, тобто перший рядок таблиці. Давайте зафіксуємо цю інформацію у дереві пошуку (мал. 23, а), у послідовності номерів вершин, які ми переглянули (1) і які ми бачимо (2, 3, 4) (мал. 23, в). Серед них поки що шуканої вершини 7 немає

Мал.23

Для подальшого пошуку перейдемо до однієї з нових вершин, які ми побачили. Це вершини 2, 3 і 4. У нашій послідовності (мал. 3, б) першою записана вершина 2, тому й перейдемо до неї. Які вершини ми бачимо з вершини 2 (мал. 1, а)? Це верши-ни 1, 3, 5 і 6. Цю саму інформацію можна отримати з другого рядка таблиці суміжності (мал. 1,6). Однак лише вершини 5 і 6 є новими, а вершини 1 і 3 ми вже бачили на попередніх кроках нашого алгоритму. Доповнимо дерево пошуку (мал. 4, а), по-слідовність переглянутих і «видимих» вершин (мал. 4, б) та множину (мал. 4, в) новою інформацією.

б) в)

Мал. 4

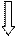Чи завершили ми наш пошук? Зрозуміло, що ні, оскільки ні у дереві пошуку, ні у послідовності ми ще не дісталися шуканої вершини 7. Тому переходимо у послідовності вершин до на-ступної «побаченої» вершини 3. Тепер її можна буде назвати не лише «побаченою», але ще й «переглянутою». Згідно із зображенням графа і відповідної йому таблиці суміжності з вершини З ми бачимо вершини 1, 2, 4 і 5. Але вони не є новими, тому ми їх не фіксуємо ні у дереві пошуку, ні у послідовності вершин, ні у множині (мал. 5, а, б, в).

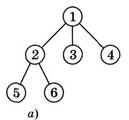
Мал.5

Переходимо до наступної вершини у послідовності, якою є вершина 4. Звідси ми бачимо вершини 1 і 3. Але і ці вершини вже є «побаченими», тому у нашому алгоритмі змінюється лише вершина, яку ми переглядаємо наступною. Такою верши­ною є вершина з номером 4, тобто наступна у нашій послідов-ності «переглянутих» і «видимих» вершин (мал. 26, б). З вер-шини 4 ми знову-таки нічого нового не побачимо, оскільки вершини 1 та 3 ми вже бачили раніше. Інформація на малюн-ках 26, а та 26, в залишилася незмінною.

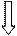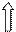
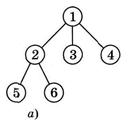
Мал.6

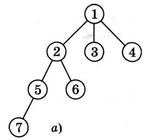
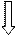Продовжуючи логіку нашого алгоритму, переходимо до вер-шини 5 - наступної у нашій послідовності (мал. 7, б). З верши-ни 5 ми бачимо вершини 2, 3, 7. Перші дві з цих вершин уже були переглянуті, а от вершина 7 не тільки нова, але й ще шука-на. Тому алгоритм можна вважати завершеним, а відповідь на поставлене на початку запитання буде такою: «У заданому графі вершина 7 є досяжною з вершини 1».

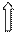Мал.7

Проаналізуємо описаний алгоритм з точки зору його ре-алізації у вигляді програми. Як було вже сказано вище, інфор-мація про граф міститиметься у таблиці суміжності або у списку суміжності. Інформація про «переглянуті» і «побачені» верши-ни - в одновимірному масиві. Алгоритм обробки цього масиву відповідає роботі зі структурою даних «черга», де «голова» чер-ги вказує на поточну вершину, з якої ми дивимося далі, а «хвіст» вказує на останню видиму вершину. Під час виконання алгоритму «голова» переміщується вправо на нову вершину, в яку ми переходимо для подальшого перегляду нових вершин, а «хвіст» також переміщується вправо одночасно з дописуван-ням нових видимих вершин.

Тепер ми можемо проаналізувати умови завершення роботи алгоритму пошуку в ширину. Таких випадків є два: шукана вершина знайдена і відомий шлях до неї, або шукана вершина є недосяжною і шлях до неї відсутній.

Ми розглянули саме перший випадок пошуку вершини в графі, коли шукана вершина 7 є досяжною із заданої вершини 1. Шлях від вершини 1 до вершини 7 присутній у черзі, але без додаткової інформації він дещо прихований. Для отримання цього шляху необхідно запам'ятовувати також і номери вер­шин, з яких ми побачили кожну наступну вершину. На малюнку 8 ця інформація позначена індексами для кожної поточної вершини, записаної у чергу.

10

21

31

41

52

62

75

Другий випадок може бути розтлумачений так: «голова» черги досягнула її «хвоста», а серед нових «побачених» вершин так і не з'явилася шукана. Це означає, що ми переглянули всі досяжні вершини графа, але не змогли дістатися до шуканої.

Підіб'ємо підсумок наших міркувань і опишемо алгоритм пошуку в ширину в словесній формі.

1. Вказати номер вершини k, з якої починається пошук за-даної шуканої вершини І.

2. Почати перегляд вершин заданого графа з вершини k, за­писавши її в чергу: і:= k. Одночасно ця вершина є і останньою «побаченою» вершиною: j:= k.

3. Зафіксувати всі нові вершини, які можна побачити з вершини і, в порядку зростання їх номерів, записуючи їх у чергу і збільшуючи при цьому на кожному кроці індекс «хвоста» чер-г и; на 1 (j:= j + 1).

4. Якщо серед нових «побачених» вершин, записаних у чергу, є шукана вершина, то перейти до п. 8.

Для переходу до перегляду наступної «побаченої» вершини збільшити значення індексу «голови» черги і (і:=і + 1).

5. Якщо значення індексу «голови» черги і збіжиться зі значенням індексу його «хвоста»; то перейти до п.10.

6. Перейти до перегляду наступної «побаченої» вершини і (п. 3).

7. Вивести інформацію про те, що шукану вершину І досягнуто і шлях до неї від вершини k існує.

8. Перейти до п. 11.

9. Вивести інформацію про те, що шукана вершина І недосяжна від вершини k і шлях до неї відсутній.

10.Завершити алгоритм.

Підіб'ємо остаточний підсумок розглянутого методу. По-перше, тепер зрозуміло, чому цей метод носить назву «пошук у ширину». Адже дійсно ми ведемо пошук шуканої вершини, роз-глядаючи на кожному новому кроці одночасно всі нові вершини по рядках таблиці суміжностей, які ще не бачили. По-друге, можна зробити висновок, що метод пошуку в ширину дає най коротший шлях від заданої вершини до шуканої. Для того щоб остаточно у цьому пересвідчитися, далі ми перейдемо до іншого методу - пошуку в глибину.

Спробуємо провести оцінку алгоритму пошуку в ширину. Під час формування черги з вершин заданого графа, що скла-дається з п вершин і т ребер, кожна вершина переглядається лише один раз. Це відповідає оцінці О(п). Але при цьому пере-глядаються всі ребра, яким належить поточна вершина. Отже, оцінка перегляду ребер становить О(т). Оскільки перегляд ребер іде паралельно з переглядом вершин, що їм належать, то остаточна оцінка алгоритму визначається як 0(п + пі). Отже, можна зробити висновок, що час роботи алгоритму прямо пропорційний розміру заданого графа.

Дата добавления: 2014-01-07