Влияние на адсорбцию на границе раствор-газ строения и размера молекул ПАВ. Правило Траубе, его аналитическое выражение и физическое обоснование

Переход от изотермы поверхностного натяжения к изотерме адсорбции графическим методом, расчет величины Гмах с помощью уравнения Ленгмюра.

σ tgα=-(z/c)= Г с/Г сtgα=Гмах Г Г=ГмахКС/1+КС

=-(dσ/dc) α Гмах→S₀=

z Г= =1/ГмахNa→δ₀=МГмах/ρ

с c c c

Правило Дюкло-Траубе. Величина поверхностной активности (g) ↑ при ↓ полярности углеводородного радикала. g в гомологическом ряду ПАВ изменяется в геометрической прогрессии при увеличении длины цепи в арифметической прогрессии. При увеличении длинны цепи ↓ растворимость ПАВ и ↑ адсорбция.

σ Г Гмах=const

σ₀

уксусная кислота(С₂) С₅

пропионовая кислота (С₃) С₄

масляная к-та(С₄) С₃

валериановая кислота(С₅) С₂

с с

При увеличении длинны цепи в гомологическом ряду алифатического соединения на одну группу СН₂, поверхностная активность ↑ в 3,2 раза(относится к водным растворам при комнатной температуре) Аналитическое выражение q_n+1/q_n=3.2

К_n+1/K_n=3.2. Физический смысл А=RTlnK. Работа адсорбции- работа обратимого переноса 1 моля вещества из объема в 1 поверхностный слой. A_n+1-A_n=RTlnK_n+1-RTlnK_n=

=690кал/моль К_n+1/K_n=3.2. сущность этого правила состоит в том, что работа адсорбции на каждую группу СН₂-const=690кал/моль.

18. Уравнение Шишковского, связь с его помощью уравнений Ленгмюра и Гиббса.

σ

σ₀ 1 2 3 1 и 3- прямые 2-переходный

σ=σ₀-σ₀Bln(C/A +1) константа В- постоянная величина в ряду гомологов

В=0,15-0,3; const 1/А- удельная капиллярная с постоянная, изменяется в ряду

гомологов ак же как на поверхностно активных. 1-«С» мала ln(C/A +1)≈C/A

σ=σ₀-σ₀BlnC/A -d σ= σ₀B (dC/A)

-(dσ/dC)≈1/A. Определение константы уравнения Шишковского, рассмотрим участок 2: σ=σ₀-σ₀BlnC/A- уравнение прямой линии в координатах σ lnC.

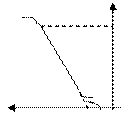-ln(1/A) σ tgα=-σ₀β→tg(180-α)= σ₀β→если σ=σ₀, то σ₀BlnC/A=0→lnC=-ln(1/A)

σ ₀ →Гмах= K=1/A 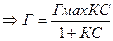Связь уравнений Ленгмюра и Гиббса с

α помощью уравнения Шишковского:

lnC разделим и проинтегрируем σ=σ₀-ГмахRTln(1+КС)→ГмахRT=σ₀B. K=1/A.т.о., у-ния, описывающие изотермы адсорбции и поверхностного натяжения, взаимосвязаны между собой.(к 19).

19. Построение изотермы адсорбции по изотерме поверхностного натяжения расчетным путем с помощью уравнения Шишковского. Связь между константами уравнения Шишковского и Ленгмюра. (см 18)

Переход от уравнения Гиббса к уравнению Ленгмюра с

lnC α помощью уравнения Шишковского:

-dσ=σ₀-σ₀Bln(C+A)= σ₀В-(dC/C+A)

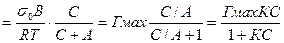-показывает общность теории адсорбции, вывод на основании разных представлений. 2-ой вид уравнения Шишковского:σ=σ₀-ГмахRTln(1+КС)

Дата добавления: 2014-01-06