
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Швидкості точок тіла
|
|
|
|
Знайдемо спочатку розподіл швидкостей у вільному твердому тілі. Згідно із законом про розподіл швидкостей та прискорень зробимо висновок про характер руху тіла.
Введемо у розгляд дві системи координат (див. рис. 5.1), одна з яких є нерухомою ( ), а друга – жорстко зв'язана з тілом (
), а друга – жорстко зв'язана з тілом ( ).
).
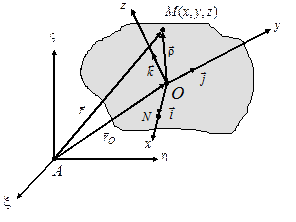
| Виберемо у тілі довільну т. і знайдемо її швидкість. Положення т. і знайдемо її швидкість. Положення т. 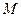 в цих двох системах координат визначимо векторним способом. Нехай вектор в цих двох системах координат визначимо векторним способом. Нехай вектор  визначає положення т. визначає положення т. 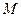 в рухомій с. к. ( в рухомій с. к. ( ). Положення т. ). Положення т. 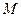 в нерухомій с. к. буде визначатися вектором в нерухомій с. к. буде визначатися вектором 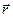 . З рисунку випливає, що . З рисунку випливає, що
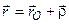 .
Розкладемо вектор .
Розкладемо вектор  за ортами рухомої с. к.: за ортами рухомої с. к.:
|
| Рис. 7.1.Системи координат. | 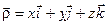 , (7.1) , (7.1)
|
тоді
 , ,
| (7.2) |
і, диференціюючи цей вираз за часом, отримаємо

| (7.3) |
(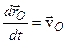 ).
).
Знайдемо похідні від одиничних векторів. Для цього розглянемо дві системи рівнянь:
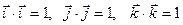 ; ;
| (7.4) |
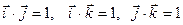 . .
| (7.5) |
Диференціюємо першу рівність системи (7.4) за часом:
 . .
| (7.6) |
Тут  - швидкість точки
- швидкість точки  кінця вектора
кінця вектора 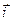 (точки, що окреслює годограф орта
(точки, що окреслює годограф орта 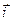 ). На підставі рівності (7.6) вектор
). На підставі рівності (7.6) вектор  . Але оскільки
. Але оскільки  , тобто
, тобто 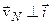 , то, очевидно, вектор
, то, очевидно, вектор 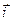 здійснює обертальний рух і тоді
здійснює обертальний рух і тоді

| (7.7) |
згідно з формулою Ейлера. Тут  - невідома кутова швидкість орта
- невідома кутова швидкість орта 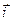 .
.
Для двох інших рівностей системи (7.4) отримуємо
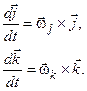
| (7.8) |
Щоб знайти  , розглянемо рівності (7.5). Диференціюючи першу з них, отримаємо
, розглянемо рівності (7.5). Диференціюючи першу з них, отримаємо
 . .
| (7.9) |
Підставляючи у вираз (7.9) рівності (7.7) і (7.8), будемо мати
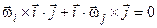 ,
,
звідки легко знайти (використовуючи правило циклічної перестановки у змішаному добутку: 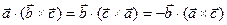 і комутативність скалярного добутку), що
і комутативність скалярного добутку), що
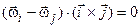 . .
| (7.10) |
Рівність (7.10) є вірною тільки якщо 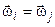 , оскільки окрім того, що
, оскільки окрім того, що 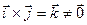 вірно й те, що вектори
вірно й те, що вектори 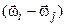 і
і  в загальному випадку не є ортогональними.
в загальному випадку не є ортогональними.
Якщо досліджувати аналогічним чином інші рівності (7.5), то неважко встановити, що
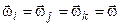 ,
,
тоді похідні від ортів можна переписати так:
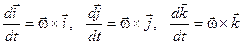 . .
| (7.11) |
Підставимо формули (7.11) в (7.3):
 .
.
Отже, отримали
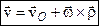 , - , -
| (7.12) |
закон розподілу швидкостей у вільному твердому тілі.
Фізичний зміст вектора 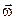 поки що невизначений, але можна відмітити, що за умови
поки що невизначений, але можна відмітити, що за умови 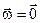 :
: 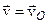 , тобто тіло здійснює поступальний рух, а при
, тобто тіло здійснює поступальний рух, а при 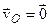 (що відповідає «закріпленню» тіла у точці
(що відповідає «закріпленню» тіла у точці 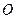 ) формула (7.12) переходить у формулу Ейлера (однак при цьому ми не можемо стверджувати, що вісь обертання є нерухомою).
) формула (7.12) переходить у формулу Ейлера (однак при цьому ми не можемо стверджувати, що вісь обертання є нерухомою).
Із формули (7.12) дістаємо висновок: рух вільного твердого тіла можна уявити як складений з двох рухів: поступального разом із полюсом 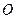 і обертального навколо деякої осі, що проходить через полюс
і обертального навколо деякої осі, що проходить через полюс 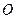 . Ця вісь називається миттєвою віссю обертання, вона змінює у просторі своє положення і напрямок, а
. Ця вісь називається миттєвою віссю обертання, вона змінює у просторі своє положення і напрямок, а 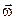 є миттєвою кутовою швидкістю. Відмітимо також, що вектори
є миттєвою кутовою швидкістю. Відмітимо також, що вектори 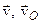 і
і  не лежать в одній площині.
не лежать в одній площині.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 229; Нарушение авторских прав?; Мы поможем в написании вашей работы!