Конвективний теплообмін

Конвекцією називається перенос теплоти при переміщенні і перемішуванні всієї маси нерівномірно нагрітих рідини чи газу. При цьому, перенос теплоти залежить від швидкості руху рідини чи газу прямо пропорційно. Цей вид передачі теплоти супроводжується завжди теплопровідністю, яка має місце, наприклад, в граничному ламінарному шарі товщиною 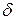чи ламінарному підшарі товщиною турбулентного граничного шару (рис.8.1) при обтіканні середовищем твердого тіла.

Рис.8.1. Схема динамічного граничного шару.

Одночасний перенос теплоти конвекцією і теплопровідністю називається конвективним теплообміном.

В інженерних розрахунках часто визначають конвективний теплообмін між потоками рідини чи газу і поверхнею твердого тіла. Цей процес конвективного теплообміну називають конвективною тепловіддачею або просто тепловіддачею.

Диференціальні рівняння конвекції. Процес конвективного теплообміну між поверхнею тіла і середовищем (рідиною або газом) описується законом Ньютона-Ріхмана або диференціальним рівнянням тепловіддачі, згідно з яким, кількість теплоти, переданої від рухомого середовища до поверхні твердого тіла і навпаки прямо пропорційна різниці температур поверхні тіла і середовища:

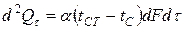, (8.1)

де 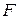– площа теплообміну; – час; a - коефіцієнт тепловіддачі,Вт/м²·К; – температура поверхні тіла; 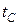– температура середовища.

Цю ж теплоту можна визначити за законом Фур’є як теплоту, що проходить через ламінарний шар чи підшар теплопровідністю:

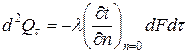. (8.2)

Густина теплового потоку за законом Ньютона-Ріхмана:

, (8.3)

Перенос тепла в рухомому середовищі описується диференціальним рівнянням конфекції (рівнянням Фур’є-Кірхгофа):

, (8.4)

де – компоненти вектора швидкості W на координатні осі x, y, z, а – коефіцієнт температуропровідності; 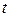– температура; – час; q_v - потужність внутрішнього джерела (стоку) тепла Вт/м³; с_р - теплоємність при постійному тиску, кДж/кг·К; r - густина середовища, кг/м³.

Рух середовища в процесі конвективного теплообміну описується рівнянням руху в’язкої рідини (Нав’є – Стокса), проекція якого на вісь :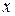

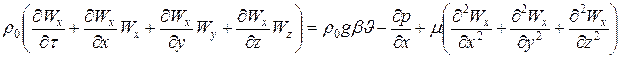, (8.5)

де 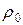– густина середовища при температурі 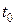; 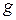– прискорення вільного падіння; 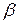– коефіцієнт об’ємного розширення (для ідеального газу ); .

Закон збереження маси щодо елементарного об’єму середовища виражається рівнянням нерозривності:

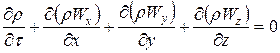. (8.6)

Наведені рівняння разом з умовами однозначності дозволяють аналітично досліджувати задачі конвективного теплообміну в будь-якому конкретному випадку. Рішення цих диференціальних рівнянь складна і трудомістка задача, і вона можлива при обмежених простих випадків. Тому при дослідженні конвективного теплообміну застосовують метод теорії подібності.

Основи теорії подібності. Теорія подібності – це наука про подібні явища. Явища подібні, якщо вони мають подібні умови однозначності і чисельно однакові визначальні критерії подібності.

Подібними явищами називаються такі фізичні явища, що однакові якісно за формою і змістом, тобто мають одну фізичну природу, розвиваються під дією однакових сил і описуються однаковими за формою диференціальними рівняннями і крайовими умовами.

Обов'язковою умовою подібності фізичних явищ повинна бути геометрична подібність систем, де ці явища протікають. Два фізичних явища будуть подібні лише в тому випадку, якщо будуть подібні усі величини, що характеризують їх. Для всіх подібних систем існують безрозмірні комплекси величин, що називаються критеріями подібності.

Основні положення теорії подібності формулюють у вигляді 3-х теорем.

1 теорема: Подібні явища мають однакові критерії подібності.

2 теорема: Будь-яка залежність між змінними, що характеризує будь-які явища, може бути представлена, у формі залежності між критеріями подібності, складеними з цих змінних, котра буде називатися критериальным рівнянням.

3 теорема: Два явища подібні, якщо вони мають подібні умови однозначності і чисельно однакові визначальні критерії подібності.

Умовами однозначності є:

· наявність геометричної подібності систем;

· наявність однакових диференціальних рівнянь;

· існування єдиного рішення рівняння при заданих граничних умовах;

· відомі чисельні значення коефіцієнтів і фізичних параметрів.

За допомогою теорії подібності визначається коефіцієнт тепловіддачі, який є функцією багатьох параметрів:

α = f₁(Х; Ф; l_o; x_c; y_c; z_c; W_o; Δt; λ; а; с_р; ρ; ν; β), (8.7)

де: Х – характер руху середовища (вільний, примусовий);
Ф – форма поверхні;
l_o – характерний розмір поверхні (довжина, висота, діаметр і т.д.);
x_c; y_c; z_c – координати;
W_o – швидкість середовища (рідина, газ);
Δt = (t_'ст - t_'с) – температурний напір;
λ – коефіцієнт теплопровідності середовища;
а – коефіцієнт температуропровідності середовища;
с_р -ізобарна питома теплоємність середовища;
ρ -густина середовища;
ν= μ / r – коефіцієнт кінематичної в'язкості середовища; (μ – коефіцієнт динамічної в'язкості; r – густина середовища);

β – температурний коефіцієнт об'ємного розширення середовища.

Безрозмірний коефіцієнт тепловіддачі, згідно з теорією подоби, розраховується за допомогою критеріального рівняння, яке складається основі експериментальних досліджень для кожного конкретного виду конвективного теплообміну:

Nu = f₂(Х; Ф; X₀; Y₀; Z₀; Re; Gr; Pr), (8.8)

де: X₀; Y₀; Z₀ – безрозмірні координати;
Nu = α·l₀/λ - критерій Нуссельта (безрозмірний коефіцієнт тепловіддачі), характеризує теплообмін між поверхнею стінки і рідиною (газом);
Re = W·l₀/ν - критерій Рейнольдса, характеризує співвідношення сил інерції і в'язкості і визначає характер течії рідини (газу);
Gr = (β·g·l₀³·Δt)/ν² - критерій Грасгофа, характеризує подйомну силу, що виникає в рідині (газі) унаслідок різниці густин;
Pr = ν/а = (μ·c_p)/λ - критерій Прандтля, характеризує фізичні властивості рідини (газу).

Після визначення критерію Нуссельта розраховується величина коефіцієнта тепловіддачі: .

Для розрахунку безрозмірного коефіцієнта тепловіддачі використовуються основні розрахункові формули конвективного теплообміну, що дані для середніх значень коефіцієнтів тепловіддачі по поверхні стінки.

Вільна конвекція. В необмеженому просторі (рис.8.2. а):

а). Горизонтальна труба діаметром d при 10³<(Gr· · Pr) <10⁸.

Nu= 0,5·(Gr·Pr)^0,25 (Pr_с/Pr_ст)^0,25. (8.9)

б). Вертикальна труба і пластина:
1). ламінарна течія - 10³<(Gr · Pr) <10⁹:

Nu= 0,75·(Gr·Pr)^0,25·(Pr_с/Pr_ст)^0,25. (8.10)

2). турбулентна течія - (Gr · Pr) > 10⁹:

Nu= 0,15· (Gr·Pr)^0,33 ·(Pr_с/Pr_ст)^0,25. (8.11)

а) б)

Рис.8.2. Зміна по висоті стінки при вільній конвекції в необмеженому просторі (а) і вільна конвекція в обмеженому об’ємі (б)

Тут значення Gr, Pr і Pr_с беруться при температурі рідини (газу), а Pr_ст при температурі поверхні стінки. Визначальна температура – температура середовища; визначальний лінійний розмір для горизонтальних труб – діаметр, вертикальних поверхонь – висота.

в). Горизонтальна пластина: розрахункове значення Nu збільшується на 30%, якщо нагріта поверхня зорієнтована вверх і на 30% зменшується, якщо нагріта поверхня зорієнтована вниз. Визначальний розмір – менша сторона пластини. Для повітря Pr_с/Pr_ст = 1 і наведені формули спрощуються.

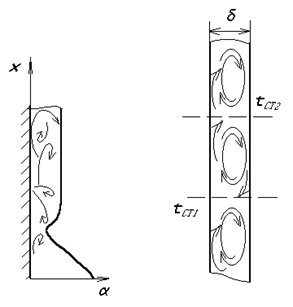
В обмеженому просторі (рис.8.2. б) середня густина теплового потоку розраховується за формулами теплопровідності із заміною коефіцієнта теплопровідності 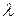середовища еквівалентним 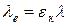. Якщо 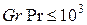, приймається . В області 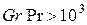приймається .

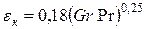Визначальний розмір – ширина каналу, визначальна температура – середня температура середовища. Густина теплового потоку: .

Примусова конвекція. Режим течії (рис.8.3) визначається по величині Re.

а) б)

Рис.8.3. Схеми ламінарної (а) і турбулентної (б) течії рідини в трубах.

а). Течія рідини в гладких трубах круглого перетину.

1). ламінарна течія (рис. 3.а) – Re < 2100

Nu= 0,15·Re^0,33·Pr^0,33·(Gr·Pr)^0,1·(Pr_с/Pr_ст)^0,25·ε_l (8.12)

або 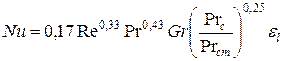, (8.13)

де ε_l - коефіцієнт, що враховує зміну середнього коефіцієнта тепловіддачі по довжині труби і залежить від відношення довжини труби до його діаметра (l/d). Значення цього коефіцієнта представлені в таблиці 8.1.

Таблиця 8.1.

Значення ε_l при ламінарному режимі.

l/d
εl	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1,0

2). перехідний режим – 2100 < Re < 10⁴

Nu= К₀·Pr^0,43·(Pr_с/Pr_ст)^0,25·ε_l . (8.14)

Коефіцієнт К₀ залежить від критерію Рейнольдса Re і представлена в таблиці 8.2.

Таблиця 8.2.

Значення К₀.

Re?10^4	2,1	2,2	2,3	2,4	2,5
ДО0	1,9	2,2	3,3	3,8	4,4	6,0	10,3	15,5	19,5	27,0	33,3

3). турбулентна течія (рис.8.3.б) – Re = 10⁴

Nu = 0,021· Re^0,8·Pr^0,43· (Pr_с/Pr_ст)^0,25·ε_l . (8.15)

Значення коефіцієнта ε_l представлені в таблиці 8.3.

Таблиця 8.3.

Значення ε_l при турбулентному режимі.

l/d	εl
Re = 2·10^3	Re = 2·10^4	Re = 2·10^5
	1,9	1,51	1,28
	1,70	1,40	1,22
	1,44	1,27	1,15
	1,28	1,18	1,10
	1,18	1,13	1,08
	1,13	1,11	1,06
	1,05	1,05	1,03
	1,02	1,02	1,02
	1,00	1,00	1,00

б).Обтікання горизонтальної поверхні.
1). ламінарна течія – Re < 4 · 10⁴

Nu= 0,66·Re^0,5·Pr^0,33 ·(Pr_с/Pr_ст)^0,25. (8.16)

2). турбулентна течія – Re > 4·10⁴

Nu = 0,037·Re^0,5·Pr^0,33 ·(Pr_с/Pr_ст)^0,25. (8.17)

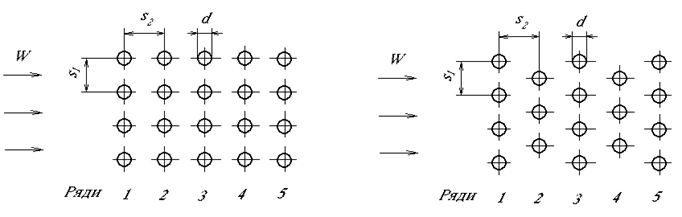Теплообмін при поперечному обтіканні. а). Пучки труб (рис.8.4) (кут атаки j = 90⁰). Використувються два види розташування труб в пучках: коридорне (рис.8.4. а) і шахового (рис.8.4. б).

а) б)

Рис.8.4. Схеми розташування труб в пучках.

Середній коефіцієнт тепловіддачі при може бути визначений з рівняння:

. (8.18)

Для шахового пучка 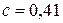; ; для коридорного ; .

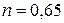Коефіцієнт, який враховує вплив відносних поперечного 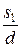і поздовжнього 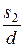кроків для коридорного пучка 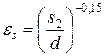; для шахового при ; при .

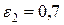Коефіцієнт, який враховує номер ряду для першого ряду ; для другого ряду шахового пучка коридорного ; для третього і наступних рядів .

За визначальну температуру приймається середня температура середовища, визначальний розмір – зовнішній діаметр труби, швидкість течії середовища – швидкість в самому вузькому перетині ряду труб.

Середнє значення коефіцієнта тепловіддачі:

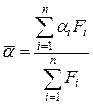, (8.19)

де – середній коефіцієнт тепловіддачі 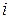-го ряду; 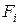– сумарна площа поверхні труб 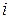-го ряду; – число рядів у пучку.

б). Поперечне обтікання одиночної труби.
1). при Re = 5 - 10³

Nu= 0,57·Re^0,5·Pr^0,38 ·(Pr_с/Pr_ст)^0,25. (8.20)

2). при Re = 10³ - 2·10⁵

Nu = 0,25 Re^0,6·Pr^0,38 ·(Pr_с/Pr_ст)^0,25. (8.21)

Теплообмін при кипінні. При бульбашковому кипінні (т.А-т.К на рис.8.5) теплообмін описується рівнянням:

, (8.22)

де – критерій кипіння; – питома теплота випаровування; 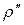– густина пари; – відривний діаметр бульбашок; 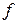– частота видривання бульбашок. За визначальний геометричний розмір прийнята капілярна стала ; 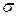– напруження поверхневого натягу; 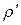– густина рідини.

Для води в т.А (рис.8.5) ; в т.К 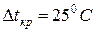, , 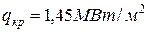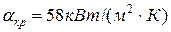; правіше т.В, ; .

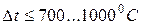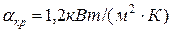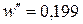Добуток характеризує середню швидкість росту бульбашок пари , яка залежить від тиску. При тиску 0,1МПа для води м/с, етилового спирту м/с. Для різних рідин наближене значення 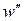можна знайти за емпіричною формулою:

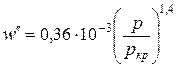, (8.23)

де 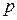– тиск рідини; 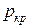– критичний тиск.

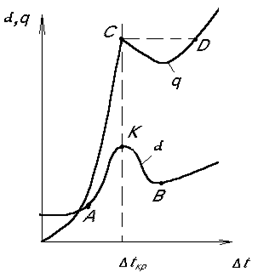Рис.8.5. Характер зміни і при кипінні.

На рис.8.5 (лівіше т.А має місце вільна конвекція; в інтервалі т.А – т.К – бульбашкове кипіння; в інтервалі т.К – т.В – неусталене плівкове кипіння; правіше т.В усталене плівкове кипіння).

Для розрахунку теплообміну при одночасному впливі швидкості примусового руху рідини і кипіння використовується емпірична залежність:

, (8.24)

де – шуканий коефіцієнт тепловіддачі; 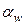– коефіцієнт тепловіддачі при примусовому русі без кипіння; 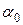– коефіцієнт тепловіддачі при розвинутому кипінні.

Теплообмін при конденсації. При конденсаці насищеної пари і ламінарній течії плівки конденсату (рис.8.6) за нехтування конвективним переносом теплоти в ній густина теплового потоку:

; (8.25)

або 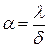, (8.26)

де 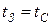– температура зовнішньої поверхні плівки конденсату; 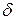– товщина плівки; 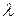– коефіцієнт теплопровідності конденсату.

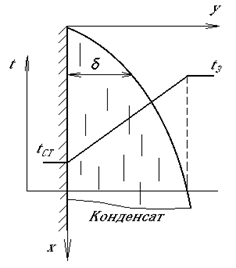Рис.8.6. Схема плівкової конденсації

Для визначення середнього значення при утворенні на поверхні твердого тіла плівки конденсату використовують рівняння:

, (8.27)

де – критерій Галілея; 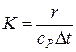– критерій фазового переходу; ; 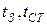– температури поверхонь плівки конденсату і твердого тіла (стінки).

Фізичні параметри плівки конденсату визначаються при температурі 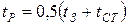, теплота пароутворення при температурі . Для вертикальних труб чи стінки , для горизонтальних труб . Вплив перегріву пари може бути врахований шляхом підстановки замість величини 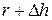, де 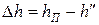– теплота перегріву пари; – ентальпія рідини, що кипить; – ентальпія сухої насиченої пари.

Визначальний для вертикальних стінки чи труби визначальний розмір – їх висота, для горизонтальних – менший розмір пластини і діаметр труби.

Дата добавления: 2014-01-07