Композиция законов распределенияНаиболее достоверным способом суммирования является композиция законов распределения

Ø Исходными данными о суммируемых погрешностях являются их полные вероятностные характеристики,
т.е. плотности вероятностей или функции распределения.

Ø Задача состоит в том, что бы найти закон распределения суммы случайных погрешностей.

Ø 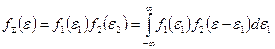Закон распределения суммы случайных величин представляет собой композицию законов распределения,
которая находится с помощью свертки:

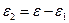где – плотности вероятностей суммы и плотности вероятностей слагаемых,

Ø 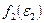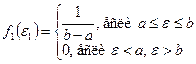5.1. Композиция двух законов распределения, один из которых характеризуется равномерной функцией плотности распределения

а другой – непрерывной функцией плотности распределения

Ø 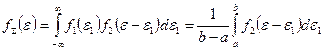Плотность вероятности суммы этих двух случайных погрешностей (композиция) определяется выражением:

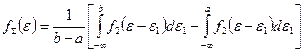Ø 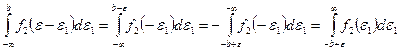Учитывая, что

Ø Отсюда

Ø Таким образом,

Ø Графическая интерпретация

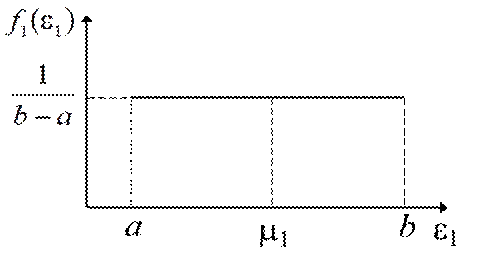
Ø Из полученного выражения следует, что композиция представляет собой разность смещенных друг относительно друга на (b – a) интегральных функций распределения второй составляющей.

Ø Умножение на коэффициент делает результат нормированным, т.е. позволяет получить под построенной кривой площадь, равную единице.

5.1.1. Композиция двух законов распределения,
каждый из которых характеризуется равномерной функцией плотности распределения (при)

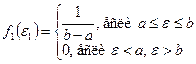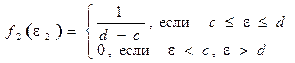
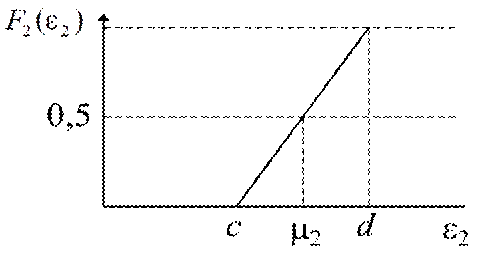
Ø Для построения результирующего закона распределения отметим на оси абсцисс точки a; b; a+ m₂; m₁; m₁ + m₂; b+ m₂. Вокруг точек a+ m₂ и b+ m₂ построим две кривые интегральной функции F ₂(e – a) и F ₂(e – b), как это показано на рисунке:

Ø Частный случай – при
треугольный закон (закон Симпсона)

Ø 5.1.2. Композиция двух законов распределения, первый
из которых характеризуется равномерной функцией плотности распределения, а второй – нормальной

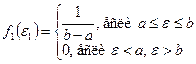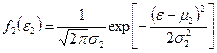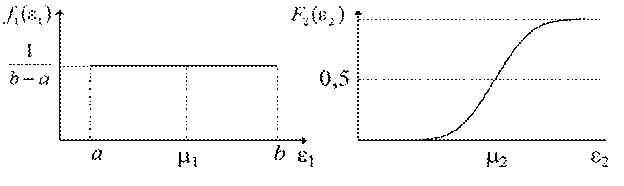
Ø Для построения результирующего закона распределения отметим на оси абсцисс точки a; b; a+ m₂; m₁; m₁ + m₂; b+ m₂. Вокруг точек a+ m₂ и b+ m₂ построим две кривые интегральной функции F ₂(e – a) и F ₂(e – b), как это показано на рисунке:

Ø 5.2. Композиция двух законов распределения, каждый
из которых характеризуется нормальной функцией плотности распределения

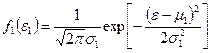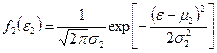Ø 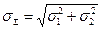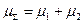даёт закон распределения, характеризующийся нормальной функцией плотности распределения
с характеристиками и

Ø В итоге

Дата добавления: 2014-01-06