Дроселювання газів і пари. Диференціальний та інтегральний дросель ефект. Інверсія. Дроселювання водяної пари

Основні поняття та визначення. Рівняння першого закону термодинаміки для потоку речовини. Технічна та наявна роботи. Оборотне витікання газів та пари через сопла та дифузори.Швидкість витікання і масова витрата ідеального газу через сопла. Аналіз рівняння масової витрати ідеального газу і критичний тиск. Критична швидкість і максимальна витрата ідеального газу при витіканні через сопло. Основні закономірності течії ідеального газу по каналам змінного перерізу (у соплах та дифузорах). Випадки витікання ідеального газу зі звуженого сопла. Витікання ідеального газу з комбінованого сопла Лаваля. Витікання газів з урахуванням тертя (дійсний процес витікання). Витікання водяної пари.

Джерела інформації: [1], с.197-236; [2] с. 86-94; [8], с.325-333;

Основні поняття та визначення. У багатьох галузях техніки широко застосовуються машини та апарати, у яких робоче тіло перебуває у безперервному русі (потоку). При цьому речовина надходить до одного місця системи зі швидкістю w ₁ і параметрами р ₁, v ₁, Т ₁, а в іншому – видаляється зі швидкістю w ₂ і параметрами р ₂, v ₂, Т ₂. Приклади таких систем: ділянка каналу змінного перерізу, парові та газові турбіни, компресори, парові котли та інші теплообмінні пристрої.

Для термодинамічного аналізу потоку приймаються такі припущення:

змінну за поперечним перерізом потоку швидкість (біля стінки каналу вона дорівнює нулю і максимальна на вісі каналу) замінюють середнім значенням w, яке визначається виразом

,

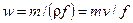де m - масова витрата; ρ - густина потоку; f - площа поперечного перерізу каналу;

розглядають тільки такий потік, у якому швидкість і інші параметри у кожному його перерізі не змінюються у часі, тобто стаціонарнийпотік, який характеризується сталою масовою витратою

або mv = fw.

(9.1)

Рівняння (9.1) відображає умову нерозривності (суцільності) потоку. Якщо злогарифмувати, а потім здиференціювати це рівняння при , отримаємо рівняння нерозривності у диференціальній формі

(9.2)

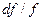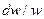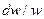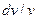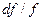Рівняння (9.2) установлює зв’язок між степенем зміни перерізу (профілю) каналу , степенем зміни об’єму dv / v і швидкості потоку . Якщо > , то < 0, тобто канал має звужуватися; якщ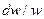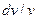о < , то 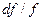> 0, тобто канал має розширюватися; якщ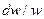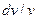о = , то 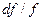= 0, тобто канал повинен мати незмінний переріз (цей випадок характеризує течію краплинної рідини, для якої dv = 0).

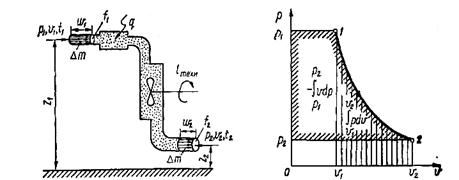
Рівняння першого закону термодинаміки для потоку речовини. Розглянемо відкриту (проточну) систему зі стаціонарним потоком речовини (рис. 9.1), до якої підводиться питома теплота q, а також підводиться (у компресорі) або відводиться (у турбіні) питома технічна робота на валу l _техн. Технічна робота – це робота робочого тіла у проточній системі, яка не пов’язана з дефомацією границь системи, тобто зміною її об’єму Ця робота, наприклад, здійснюється газом при обертанні ротора турбіни. На відміну від закритих у відкритих системах потік робочого тіла несе з собою крім внутрішньої енергії також і кінетичну енергію свого руху відносно границь системи. У деяких випадках необхідно ураховувати зміну потенціальної енергії робочого тіла у полі зовнішніх сил. При введенні робочого тіла необхідно долати дію внутрішнього тиску у системі. Отже, над робочим тілом, що надходить до системи, має бути здійснена деяка робота зовнішньої сили – робота введення (-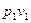), яка збільшує повну енергію системи. При виведенні робочого тіла з системи має витрачатися робота на подолання тиску зовнішнього середовища – робота виведення робочого тіла (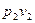). Роботу введення – виведення робочого тіла називають роботою проштовхування

.

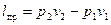Математичний вираз першого закону термодинаміки для потоку у інтегральній формі:

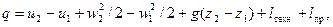
або з урахуванням того, що ,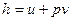

(9.3)

У диференціальній формі

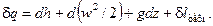(9.4)

Отже, теплота, що підводиться до потоку речовини, витрачається на зміну ентальпії, кінетичної і потенціальної енергії речовини, а також на виконання технічної роботи.

У багатьох випадках зміною потенціальної енергії можна знехтувати, а отже рівняння (9.3) набуде вигляду

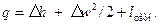
(9.5)

Якщо зіставити рівняння (9.5) з рівнянням першого закону термодинаміки для закритої системи, отримаємо

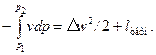
(9.6)

Інтеграл у (9.6) зображається у p – v координатах (рис. 9.2) площею 12p₂ p₁ і являє собою частину питомої роботи зміни об’єму робочого тіла, яка може бути корисно використана на зміну його питомої кінетичної енергії і виконання питомої технічної роботи. У зв’язку з цим інтеграл (9.6) називають питомою наявною роботою:

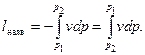(9.7)

Питома наявна робота політропного процесу визначається за формулою (4.32).

  Рис. 9.1. Схема відкритої термодина- Рис. 9.2. Графічне зображення мічної системи наявної роботи

Якщо зіставити рівняння (9.6) і (9.7), вираз першого закону термодинаміки для потоку можна записати у такому виді:

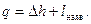
(9.8)

Оборотне витікання газів та пари через сопла та дифузори. Течія газів і пари по каналах є важливою частиною робочого процесу багатьох пристроїв в енергетичних установках, головним чином, різних турбомашин і струминних апаратів. Канали, в яких відбувається прискорена течія газів і пари (dw > 0) зі зменшенням тиску, називаються соплами, а канали, в яких відбувається сповільнена течія газів і пари (dw < 0) і підвищення тиску – дифузорами. Сопла та дифузори бувають звуженими і розширеними. Течію в соплах часто називають витіканням. При певних умовах його можна розглядати як оборотний процес:

а) близькість станів робочого тіла в будь-якому перерізі каналу до рівноважного;

б) відсутність тертя, завихрень та інших опорів течії;

в) можливість повного обернення процесу течії при послідовних сполученнях сопел і дифузорів, тобто при сполученнях прискорених і сповільнених потоків.

Окремий випадок становить нерівноважна течія газів і пари при практично незмінній швидкості (dw = 0), але при наявності більш-менш значних місцевих опорів. Така течія

має назву дроселювання.

Технічна робота у соплах та дифузорах не здійснюється, тому рівняння першого закону термодинаміки для потоку має вигляд

(9.9)

З іншого боку, для об’єму робочого тіла, яке рухається у потоці без тертя, можна застосувати вираз першого закону термодинаміки для закритої системи

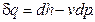
(9.10)

Якщо прирівняти праві частини двох останніх рівнянь, отримаємо

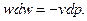
(9.11)

З (9.11) витікає, що 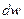і завжди мають протилежні знаки. Отже, збільшення швидкості течії у соплах (dw > 0) можливе лише при зменшенні тиску в ньому (dp < 0). Навпаки, гальмування потоку у дифузорах (dw < 0) супроводжується збільшенням тиску (dp >0).

Оскільки довжина сопел і дифузорів мала і час перебування потоку у них незначний, теплообміном між стінками цих каналів та потоком можна знехтувати і витікання вважати адіабатним (q = 0). При цьому рівняння першого закону термодинаміки для потоку (9.5) при 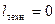прийме вигляд

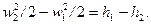
(9.12)

Отже, прискорення адіабатного потоку відбувається за рахунок зменшення ентальпії dh < 0, а сповільнення потоку викликає її збільшення (dh > 0).

Зінтегрувавши співвідношення (9.11)

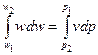
і порівнявши його з рівнянням (9.12), дістаємо, що для рівноважного адіабатного потоку

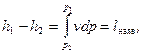
(9.13)

тобто наявна робота при адіабатному розширенні дорівнює наявному теплоперепаду .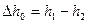

Швидкість витікання та масова витрата ідеального газу через сопла. Розглянемо процес рівноважного (без тертя) адіабатного витікання газу через сопло з резервуару, в якому газ має параметри р ₁, v ₁, Т ₁. Швидкість газу на вході до сопла позначимо через w ₁. Будемо вважати, що тиск газу на виході з сопла p ₂ дорівнює тиску середовища, в яке витікає газ.

Задачами термодинамічного аналізу витікання (розрахунку сопла) є визначення швидкості газу на виході з сопла, витрати газу, а також площі вихідного перерізу і профілю (форми) сопла.

Швидкість адіабатного витікання можна знайти з рівняння (9.12)

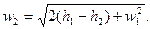
(9.14)

У багатьох випадках w ₂ >> w ₁, тоді (якщо площа вхідного перерізу сопла достатньо велика) можна прийнти w ₁ = 0 і швидкість адіабатного витікання буде дорівнювати

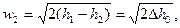
(9.15)

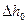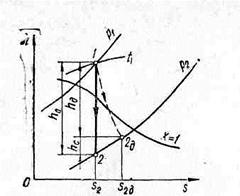
де – питомий наявний адіабатний теплоперепад. Для водяної пари 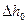зручно визначати з h – s діаграми рис. 9.3, де пряма 1-2 зображає процес адіабатного витікання. Якщо 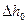виразити у кДж/кг, формула (9.15) прийме вид

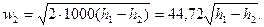
Вираз для швидкості адіабатного витікання ідеального газу можна отримати з (9.6) з урахуванням прийнятих припущень (l _техн = 0 і w ₁ = 0) і формули для наявної адіабатної роботи (4.26):

(9.16)

Масову секундну витрату газу m через сопло перерізом f ₂ (площа вихідного перерізу) можна визначити за допомогою рівняння нерозривності m = f ₂ w ₂ / v ₂, підставляючи у нього w ₂ з (9.16) і v ₂ з рівняння адіабати p ₁ v ₁ ^k = p ₂ v ₂ ^k. Отже

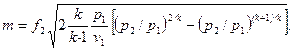
(9.17)

Аналіз рівняння масової витрати ідеального газу і критичний тиск. З виразу (9.17) витікає, що для даного ідеального газу і визначених p ₁, v ₁ масова витрата газу при витіканні залежить тільки від відношення тисків 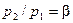_. Крива витрати газу через сопло, яка побудована за рівнянням (9.17) у вигляді 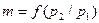, показана на рис. 9.4, а.

При р ₂ = р ₁ (β = 1) витрата дорівнює нулю (див. рис. 9.4, а). Зі зменшенням тиску середовища р ₂ витрата газу збільшується і досягає максимального значення при 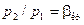. При подальшому зменшенні відношення 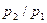значення m за формулою (9.17) зменшується і при 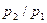= 0 стає рівним нулю. Порівняння описаної залежності з експериментальними даними показало, що для β_кр < 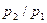< 1 результати досліду повністю збігаються з даними аналізу рівняння (9.17), а для 0 < 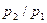< β_кр вони розходяться – дійсна масова витрата на цій ділянці залишається постійною (пряма lm).

Для пояснення цього розходження теорії з експериментом А. Сен-Венан у 1839 р. запропонував гіпотезу: у звуженому соплі неможливо отримати тиск газу нижчий критичного значення р _кр, яке відповідає максимальній витраті газу через сопло. Для значень 0 < 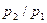< β_кр тиск у гирлі звуженого сопла перестає бути рівним тиску середовища р ₂, куди відбувається витікання, і, навіть не зважаючи на зниження тиску середовища до повного вакууму, залишається постійним і рівним критичному тиску р _кр. Для значень β_кр < 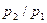< 1 тиск у гирлі звуженого сопла дорівнює тиску середовища р ₂, тому теорія збігається з дослідними даними.

Як відомо з фізики, зміна тиску (пружна деформація) розповсюджується у матеріальному стисливому середовищі зі швидкість звуку а. Тому, коли швидкість витікання менше за швидкість звуку, зменшення зовнішнього тиску середовища за соплом р ₂ досягає гирла сопла. В результаті у гирлі сопла установлюється тиск, рівний тиску середовища.

Якщо швидкість витікання досягає швидкості звуку, хвиля розрідження, яка виникає при подальшому зменшенні тиску середовища за соплом, не може передавтись до його гирла, оскільки відносна швидкість її розповсюдження (а – w) буде дорівнювати нулю. Починаючи з цього моменту тиск у гирлі сопла буде незмінним (критичним), швидкість витікання залишиться рівною швидкості звуку, а витрата газу – максимальною, не зважаючи на зниження тиску середовища за соплом. Отже швидкість витікання зі звужуваного сопла не може бути більше швидкості звуку у газі (рис. 9.4, в). Тиск p ₂ і швидкість w ₂, при яких установлюється максимальна масова витрата, називаються критичними (p _2кр, w _2кр). Критична швидкість витікання дорівнює швидкості звуку і тому її називають звуковою.

 

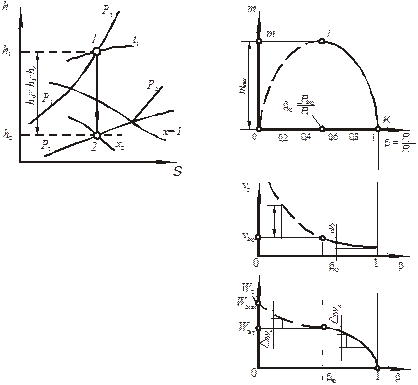
  Рис. 9.3. Процес адіабатного Рис. 9.4. Залежність секундної витрати (а), витікання водяної пари питомого об’єму (б) і швидкості витікання(в) на h – s діаграмі від перепаду тисків    

Використовуючи вираз (9.17), можна знайти значення критичного відношення тисків β_кр, при якому масова витрата середовища буде максимальною. Для цього вираз (9.17) необхідно здиференціювати по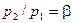і отриману похідну прирівняти до нуля. Тоді

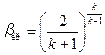
(9.18)

Величина β_кр залежить тільки від показника адіабати k, тобто від природи робочого тіла: для одноатомного газу k = 1,66 і β_кр = 0,49; для двохатомного газу k =1,4 і β_кр = 0,528; для багатоатомних газів і перегрітої пари k = 1,3 і β_кр = 0,546. швидкості

За допомогою рівняння (9.18) можна визначити критичний тиск у вихідному перерізі сопла, при якому витрата газу через сопло досягає максимальної величини

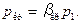
(9.19)

При заданому початковому тиску р ₁ критичний тиск р _кр – найменший тиск, який установлюється у вихідному перерізі звуженого сопла.

Критична швидкість і максимальна витрата ідеального газу при витіканні через сопло. Критична швидкість установлюється у гирлі сопла при витіканні у навколишнє середовище з тиском, який дорівнює або нижче критичного. Її можна визначити з рівняння (9.16), якщо підставити в нього замість відношення 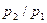значення β_кр з (9.18),

.

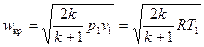(9.20)

Критична швидкість залежить тільки від природи газу та його початкових параметрів. Покажемо, що критична швидкість дорівнює швидкості звуку в газі при критичних параметрах р _кр і v _кр. З рівняння адіабати pv^k = const витікає, що v ₁ = v _кр (p _кр/ p ₁)^{1/ k}. З урахуванням (9.18) дістаємо

(9.21)

Підставляючи значення v ₁ з (9.21) і значення р ₁ з (9.19) у (9.20), отримаємо

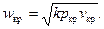
(9.22)

З курсу фізики відомо, що 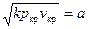є швидкість розповсюдження звуку у середовищі з параметрами р = р _кр і v = v _кр. Таким чином, критична швидкість газу при витіканні дорівнює місцевій швидкості звуку у вихідному перерізі сопла.

Максимальну секундну масову витрата газу можна визначити з рівняння (9.17) при з (9.18)

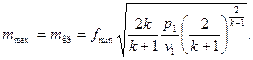
(9.22)

Максимальна витрата газу визначається станом газу на вході до сопла 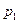і, величиною вихідного перерізу сопла 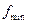і показником адіабати газу k, тобто його природою.

Основні закономірності течії ідеального газу по каналам змінного перерізу (у соплах та дифузорах). Рівняння (9.2) визначає умови нерозривності потоку і показує, що форма каналу залежить від зміни об’єму газу і його швидкості. Дослідимо це рівняння при адіабатному витіканні ідеального газу.

Після диференціювання рівняння адіабати pv^k = const отримаємо:

(9.23)

З рівняння (9.11) знаходимо

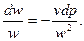
(9.24)

З урахуванням (9.23) і (9.24) рівняння (9.2) набуде вигляду

але величина kvp є квадрат швидкості звуку а ², отже

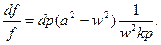
(9.25)

Проаналізуємо рівняння (9.25) стосовно двох каналів: сопла та дифузора.

Нехай рух газу здійснюється через сопло (dw > 0 і dp < 0). З рівняння (9.25) витікає, що знак df у цьому випадку протилежний знаку 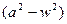. Якщо 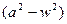> 0, w < a і df < 0: для прискореного руху в області дозвукових швидкостей переріз сопла повинен уздовж потоку зменшуватися (сопло звужене). Якщо 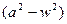< 0, w > a і df > 0: для прискореного руху в області надзвукових швидкостей переріз сопла повинен збільшуватися (сопло розширене). У самому вузькому перерізі сопла швидкість газу дорівнює швидкості звуку, що і є найбільшим значенням швидкості газу при його адіабатному витіканні зі звуженого сопла (df < 0). Для отримання надзвукових швидкостей газу в соплах наобхідно, щоб вони мали спочатку звужену частину, а потім розширену. Таке комбіноване (складене) сопло вперше було застосовано шведським інженером К.Г. Лавалем у 80-х роках минулого століття для отримання надзвукових швидкостей пари. Зараз сопла Лаваля застосовують у реактивних двигунах літаків та ракет.

Нехай рух газу здійснюється через дифузор (dw < 0 і dp > 0). З рівняння (9.25) витікає, що знак df у цьому випадку збігається зі знаком 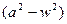. Якщо 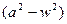> 0, w < a і df > 0: для сповільненого руху в області дозвукових швидкостей переріз дифузора повинен уздовж потоку збільшуватися. Якщо 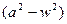< 0, w > a і df < 0: для сповільненого руху в області надзвукових швидкостей переріз дифузора повинен зменшуватися.

Таким чином, в залежності від швидкості газу на вході той самий канал може бути і соплом і дифузором. Треба підкреслити ще один істотний висновок, який характеризує особливості течії при переході через критичну швидкість (w = a): безперервний перехід швидкості руху через швидкість звуку вимагає обернення зовнішнього впливу в критичному перерізі (закон обернення впливів).

З наведеного вище випливає, що для випадку геометричного впливу на потік цей вплив (зміна площі поперечного перерізу каналу df) в критичному перерізі змінює свій знак, а величина f проходить через мінімум, тобто критичний переріз, в якому швидкість руху чисельно дорівнює місцевій швидкості звуку.

Випадки витікання ідеального газу зі звуженого сопла. Перший випадок. Тиск зовнішнього середовища більше критичного (β_кр < 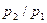< 1). При цих умовах використовується весь перепад тиску від р ₁ до р ₂ і відбувається повне розширення газу. Швидкість газу у вихідному перерізі сопла менше швидкості звуку. Тиск газу у вихідному перерізі сопла дорівнює тиску завнішнього середовища (р _вих = р ₂). Швидкість витікання і масова витрата газу при заданому вихідному перерізі визначаються за формулам (9.16) і (9.17).

Площу вихідного перерізу сопла можна визначити за формулою (9.17), якщо відома витрата m:

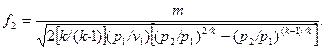
(9.26)

Другий випадок. Тиск зовнішнього середовища менше критичного (0 < 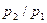< β_кр). При ціх умовах використовується не весь перепад тиску від р ₁ до р ₂, а тільки його частина від р ₁ до р _кр. Відбувається неповне розширення газу, і швидкість газу у вихідному перерізі звужуваного сопла дорівнює критичній швидкості (місцевій швидкості звуку). Тиск у гирлі сопла дорівнює критичному тиску: р _кр = р ₁β_кр. Критична швидкість витікання і максимальна витрата ідеального газу визначаються за формулами (9.20) і (9.22).

Площа вихідного перерізу сопла при заданій витраті (мінімальний переріз) визначається за формулою (9.22)

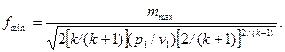
(9.27)

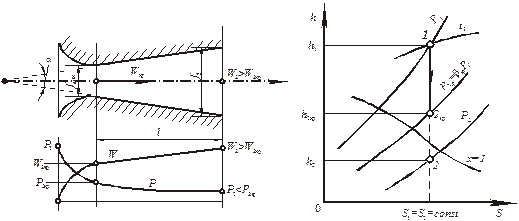
Витікання ідеального газу з комбінованого сопла Лаваля. Комбіноване сопло Лаваля призначено для використання великих перепадів тиску і для отримання швидкостей витікання, які перевищують швидкість звуку. Сопло Лаваля складається з короткої звуженої ділянки і розширеної конічної насадки (рис. 9.5). Досліди показують, що кут конусності розширеної частини має бути = 8... 12^о з умови безвідривної течії і мінімальних втрат. При більших кутах спостерігається відрив течії від стінок каналу. При витіканні газу з комбінованого сопла до навколишнього середовища з тиском менше критичного в найбільш вузькому перерізі сопла установлюються критичний тиск р _кр і критична швидкість w _кр. У розширній частині сопла відбувається подальше збільшення швидкості газу і падіння тиску до тиску зовнішнього середовища.

 

  Рис. 9.5. Комбіноване сопло Лаваля (а) Рис. 9.6. До визначення критичної та його характеристики (б) швидкості витікання водяної пари

Швидкість витікання і масова витрата ідеального газу (при заданій площі) визначаються за формулами (9.16) і (9.17). При заданій витраті площу мінімального перерізу сопла 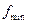можна обчислити за формулою (9.22), а площу вихідного перерізу сопла – за формулою (9.17).

Довжину звужуваної частини беруть рівною діаметру критичного перерізу сопла або з конструктивних міркувань. Довжина розширної частини сопла визначається за виразом

(9.28)

де – кут конусності сопла; D – діаметр вихідного перерізу сопла; d - діаметр сопла у мінімальному перерізі.

Витікання газів з урахуванням тертя (дійсний процес витікання). Отримані вище формули швидкості витікання і масової витрати газу справедливі тільки для оборотного процесу витікання, бо не ураховують сили тертя між робочим тілом і стінками каналу і внутрішнє тертя між струминками потоку внаслідок різниці швидкостей у перерізі каналу, а також завихрення у потоці. Наявність тертя потребує витрати частини енергії потоку на його подолання. Внаслідок цього дійсна швидкість витікання буде менше теоретичної при тому ж перепаді тиску.

Відношення дійсної швидкості газу w _д при необоротному витіканні газу з сопла до теоретичної швидкості w при оборотному витіканні при однакових початкових і кінцевих тисках і нульовій початковій швидкості називають швидкісним коефіцієнтом сопла:

φшв = w д/ w.

(9.29)

Цей коефіцієнт φ_шв, згідно з дослідними даними, для добре оброблених каналів змінюється від 0,96 до 0,98 (значення φ_шв наводять у спеціальних курсах паротурбінних установок і загальної теплотехніки).

Наявність сил тертя робить адіабатний процес необоротним. Кінетична енергія потоку, яка витрачається на подолання сил тертя, переходить у теплоту, яка сприймається робочим тілом, збільшуючи його ентальпію та ентропію при виході з каналу.

Втрати кінетичної енергії:

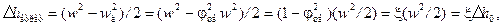
(9.30)

де 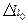– теоретичний (наявний) питомий теплоперепад.

Величину 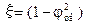називають коефіцієнтом втрати енергії (з (9.30) він дорівнює відношенню втрат у соплі до наявного теплоперепаду: 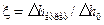). Отже дійсний корисно використаний питомий теплоперепад буде меншим за теоретичний 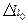на величину втрат , тобто .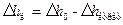

Відношення дійсної кінетичної енергії робочого тіла 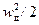до теоретичної 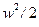називають коефіцієнтом корисної дії каналу і позначають :

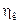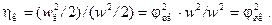
(9.31)

ККД каналу дорівнює квадрату коефіцієнта швидкості газу. Теплота тертя без урахування початкової швидкості визначається так:

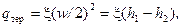
де h ₁, h ₂ - ентальпії робочого тіла на початку і в кінці оборотного адіабатного (ізоентропійного) процесу розширення. Рівняння (9.29), (9.31) справедливі для ідеального і реального газів.

Витікання водяної пари. Для водяної пари усі формули і закономірності теорії витікання ідеального газу можна застосовувати тільки для наближених обчислень, якщо вважати для перегрітої пари значення k = 1,3, а для сухої насиченої пари k = 1,135.

У випадках, коли приходиться користуватися рівняннями, у які входить показник адіабати k, його значення необхідно визначати у кожному окремому випадку за параметрам початкових і кінцевих станів процесу витікання реального газу:

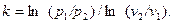
(9.32)

Найбільш доцільно обчислення швидкості витікання і масової витрати робочого тіла здійснювати за допомогою h – s діаграми даної речовини (див. рис. 9.3).

Якщо швидкість витікання менше критичної, її розраховують за формулою

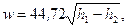
(9.33)

де h ₁ і h ₂ визначають за допомогою таблиць або h – s діаграм (в кДж/кг) за початковими параметрами і кінцевому тиску, виходячи з умови адіабатного процесу s ₁ = s ₂.

При критичному режимі витіканні (див. рис. 9.6) швидкість витікання водяної пари визначають за формулою . При цьому h ₁ (кДж/кг) береться з таблиць або h – s діаграми водяної пари за початковими параметрами. Значення ентальпії h _кр безпосередньо визначити неможливо, бо невідома величина критичного тиску. Тому рекомендується параметри пари у критичному перерізі визначати з деякою похибкою, використовуючи залежності, які справедливі для ідеального газу, методом послідовних наближень. Для цього спочатку задаються значенням k = 1,3 і за допомогою співвідношення 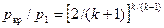знаходять р _кр. Потім з таблиць водяної пари, враховуючи, що s ₁ = s _кр, за р _кр і s _кр визначають питомий об’єм у критичному перерізі v _кр. Далі за допомогою співвідношення (9.32) при p ₂ = p _кр і v ₂ = v _кр знаходять нове значення коефіцієнта k, за яким знову обчислюють р _кр. Цю операцію повторюють до тих пір, поки значення р _кр, за яким обчислюють k, не совпаде зі значеннм його, обчисленим за формулою для р _кр / р ₁. Цей метод є наближеним, але, як показує практика, він дає у більшості випадків достатньо добрий результат.

Швидкість витікання водяної пари з комбінованого сопла обчислюють за формулою (9.33), де h ₁ – питома ентальпія водяної пари на вході до сопла, кДж/кг; h ₂ – питома ентальпія пари при параметрах середовища, куди відбувається витікання, кДж/кг. При необоротному процесі витікання 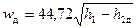. Масова витрата визначається з рівняння суцільності 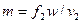; для критичного режиму витікання .

Рис. 9.7. Оборотний (1-2) і необоротний (1-2_д) процеси адіабатного витікання водяної пари

Процес витікання водяної пари на h – s діаграмі зображено на рис. 9.7: оборотний процес – лінією 1-2 і необоротний процес – умовно штриховою лінією 1 - 2 д. З рисунку бачимо, що ентальпія пари після розширення у соплі у необоротному процесі буде більше, ніж у оборотному, за рахунок теплоти тертя. Дійсний корисно використаний питомий теплоперепад буде меншим за теоретичний 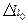на величину втрат (9.30). Якщо значення втрат відкласти уверх по адіабаті 1-2 (див. рис. 9.7) і провести горизонталь до перехрещення з ізобарою р ₂, точка 2 д буде характеризувати стан пари за соплом при дійсному процесі витікання, а штрихова крива 1 - 2 д умовно зобразить необоротне витікання.

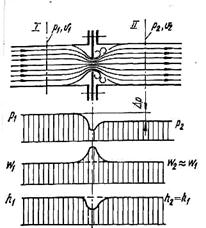
Дроселювання газів і пари. Диференціальний та інтегральний дросель ефект. Інверсія. Якщо під час руху потоку газу або пари зустрічається різке звуження перерізу каналу (не повністю відкритий вентиль або кран; зустрічається перегородка з невеликим отвором, як зображено на рис. 9.8, а), яке створює опір потоку, то в цьому місці швидкість потоку різко зростає, а тиск падає (рис. 9.8, б і в). Після звуження перерізу швидкість потоку зменшується і відновлюється до початкового значення, але тиск відновлюється не повністю.

Процес зниження тиску потоку речовини внаслідок його проходження через місцевий опір без здійснення зовнішньої роботи називають дроселюванням. Дроселювання часто застосовується в теплосилових установках при регулюванні потужності двигунів, вимірюванні витрати, у холодильній техніці. Вивчення процесу дроселювання може бути основою для одного зі способів складання рівняння стану реальних газів. Оскільки зниження тиску 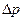пропорційно витраті газу або пари, є можливість вимірювати цю витрату. На цьому принципі працюють деякі типи витратомірів. При відсутності теплообміну (q = 0) і, якщо потік не здійснює технічну роботу (l _техн = 0), рівняння першого закону термодинаміки для потоку має вигляд

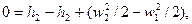
  Рис. 9.8. Дроселювання потоку речовини при проходженні через діафрагму

або

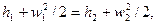
(1)

де h ₁ і h ₂ - питомі ентальпії у перерізаї І і ІІ, віддалених від місцевого опору.

При помірних швидкостях течії зміна кінетичної енергії потоку дуже мала, отже, для процесу дроселювання дістаємо

h 1 = h 2,

(2)

тобто після дроселювання ентальпія газу або пари залишається незмінною.

Користуючись далі співвідношенням для наявної роботи (9.6), знаходимо, що при дроселюванні dp < 0 або р ₂ < р ₁, тобто після дроселювання тиск газу або пари знижується, а питомий об’єм збільшується. За другим законом термодинаміки для нерівноважного адіабатного процесу ds > 0 або s ₂ > s ₁, тобто після дроселювання ентропія газу або пари більша, ніж у початковому стані. Розглянемо, як змінюється температура робочого тіла при зниженні тиску після дроселювання. Оскільки для ідеального газу h ₂ - h ₁ = c_pm (t ₂ - t ₁) на основі (2) дістаємо t ₂ = t ₁, тобто при дроселюванні ідеального газу його температура не змінюється. При дроселюванні реальних газів їх температура може зменшуватись, збільшуватись або залишатися незмінною (поведінка реальних газів значно відрізняється від поведінки ідеального). Характер і зміна температури при дроселюванні реальних газів визначаються дією міжмолекулярних сил.

Явище зміни температури реальних газів при дроселюванні вперше було виявлено Д.П. Джоулем та Дж. Томсоном у 1852 р. і отримало назву ефекту Джоуля-Томсона або дросельного ефекту.

Відношення нескінченно малої зміни температури до відповідної нескінченно малої зміни тиску при дроселюванні називають диференціальним дросель-ефектом, який виражається таким чином

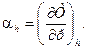
(3)

Якщо тиск і температура змінюються на скінченну величину при дроселюванні, то такий ефект називають інтегральним дросель-ефектом. Значення 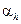визначають з диференціального рівняння

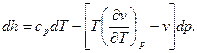
(4)

Оскільки при дроселювання dh = 0, то 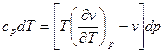, звідки

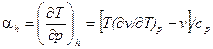
(5)

і

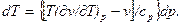
(6)

Рівняння (6) справедливе для будь-якої речовини. Для ідеального газу (дv/дT) _p = R/p = v/T, отже чисельник в рівнянні (5)

T (дv / dT)_p- v = Tv / T-v = 0,

а рівняння (5) приймає вигляд

дT/дp = 0 або dT = 0 і T ₁ =T ₂.

Отже при дроселюванні ідеального газу його температура не змінюється.

Як показує дослід, при дроселюванні реального газу його температура змінюється (ефект Джоуля-Томсона). При цьому знак диференціального дросель-ефекту для однієї й тієї ж речовини може бути додатним ((dT / дp) _h > 0) і газ охолоджується (dT < 0 бо dp < 0) і від’ємним ((дT/дp) _h < 0) і газ нагрівається (dT > 0 бо dp < 0) у різних областях стану.

Стан реального газу при адіабатному дроселюванні, у якому температурний ефект дроселювання змінює свій знак, називають точкою інверсією, а температура, при якій диференціальний дросель-ефект дорівнює нулю 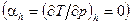, називають температурою інверсії. Якщо початкова температурі реального газу перед дроселем менше температури інверсії, то газ при дроселюванні охолоджується, якщо вище температури інверсії – нагрівається.

Для знаходження точки інверсії і умов, при яких має місце нагрівання або охолодження газу, проаналізуємо рівняння (5). При дроселюванні газу завжди dp має від’ємний знак (dp < 0), а теплоємність с_р - величина додатна. Тому знак диференціального дросель-ефекту α _h, а отже, і зміна dT, залежать від знаку виразу T (дv/дT) _p – v, а знак dT завжди йому протилежний: 1) при T (дv/дT) _p – v > 0 dT < 0; 2) при T (дv/дT) _p – v = 0 dT = 0; 3) при T (дv/дT) _p – v < 0 dT > 0. Другий випадок можна використати для отримання рівняння температури інверсії, при якій (дT/дp) _h = 0:

T (дv / дT) p - v = 0, T = v (дT / дv) p.

(7)

Цей вираз називають рівнянням кривої інверсії. Дроселювання при скінчених перепадах тисків називають інтегральним дросель-ефектом. Він визначається інтегруванням рівняння (6)

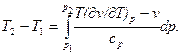
(8)

Розглянемо дроселювання газу, який підкоряється рівнянню Ван-дер-Ваальса. З рівняння Ван-дер-Ваальса 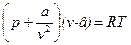знайдемо частинну похідну: (дv/дТ) _р = R /(p - a / v ² + 2 ав / v ³). Якщо підставити значення частинної похідної в рівняння (6), після декотрих припущень отримаємо наступний наближений вираз для диференціального дросель-ефекут, який справедливий при р → ∞ або при v → ∞:

α h = (dT / dp) h = (2 a/RT-b)/ cp,

(9)

де с_р – ізобарна теплоємність; а і b – сталі рівняння Ван-дер-Ваальса; R - газова стала; Т - температура газу. Оскільки при дроселюванні завжди дp < 0, а c_p > 0, знак c _p буде залежати від знаку чисельника (9). При цьому можливі три випадки:

1) dT < 0 при T < 2a /(bR) → 2a / RT - b > 0 → 2a > bRT → T < ;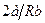

2) dT > 0 при T > ;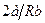

3) dT = 0 при T = .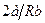

Отже, температура інверсії, де диференціальний дросель-ефект α _h = 0, дорівнює

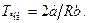
(10)

Виразимо Т _інв через критичну температуру, для чого використаємо рівняння 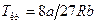, отже

.

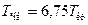Кожний реальний газ, який підкоряється рівнянню Ван-дер-Ваальса, має визначену температуру інверсії, яка при р = 0 у 6,75 разів вище критичної температури.

Температура інверсії більшості газів, за виключенням водню та гелію, у яких відповідно 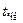= -55 ^оС і - 240 ^оС, достатньо велика, і процеси їх дроселювання звично протікають зі зменшенням температури. Більш докладний аналіз процесу дроселювання реального газу показує, що він має не одну, а безліч температур інверсії, які утворюють на p – - діаграмі так звану інверсійну криву. Рівняння інверсійної кривої, якщо маємо рівняння стану реального газу, може бути отримано у явній формі з приведеноuj раніше співвідношення. При будь-якому значенні тиску речовина має дві точки інверсії: одна з них знаходиться у області рідини, а інша - у області перегрітої пари (газу).

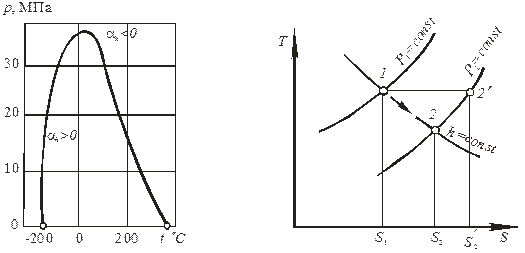
На рис. 9.9, а зображено інверсійну криву азоту. З діаграми бачимо, що будь-якому тиску відповідають дві точки інверсії при різних температурах. Крива інверсії проходить через максимум. Якщо для речовини справедливо рівняння Ван-дер-Ваальса, то з його аналізу витікає, що об’єм в точці максимуму кривої інверсії дорівнює критичному об’єму, максимальний тиск дорівнює дев’ятикратному критичному тиску, а максимальна температура дорівнює трьохкратній критичній температурі.

  а б

Рис.9.9. Інверсійна крива азоту (а) та умовне зображення процесу дроселювання потоку речовини на Т – s -діаграмі  

Інверсійна крива поділяє pT -діаграму на дві області. Всі процеси дроселювання, які починаються усередині інверсійної кривої, супроводжуються охолодженням речовини; ззовні інверсійної кривої всі процеси дроселювання протікають з нагріванням речовини. Процеси, які починаються на інверсійній кривій, відповідають випадку інверсії, коли Т ₁ = Т ₂ = Т _інв.

Теоретичні висновки щодо дросельного ефекту, які зроблені на основі рівняння Ван-дер-Ваальса, повністю підтверджуються дослідами, але з кількісного боку дають значні відхилення. З молекулярної точки зору знак зміни температури реальних газів при дроселюванні залежить від того, які сили взаємодії (притягання або відштовхування) між молекулами переважають у даному стані. Якщо переважають сили притягання (b мале у порівнянні з а в рівнянні Ван-дер-Ваальса), гази при дроселюванні будуть охолоджуватись. У випадку переваги ефекту дії сил відштовхування, гази при дроселюванні будуть нагріватися.

Оскільки процес дроселювання потоку речовини супроводжується явищами тертя і завихрення, він є необоротним і тому не може зображатися будь-яким графіком, а умовно зображається на Т – s -діаграмі штриховою лінією 1-2, яка збігається у початковій та кінцевій точках з ізоентальпою (див. рис. 9.9, б).

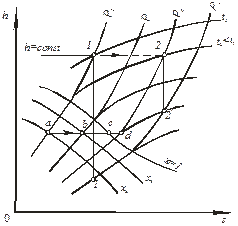
Дроселювання водяної пари.Задачі, які пов’язані з дроселюванням водяної пари, легше всього вирішуються з використанням h – s -діаграмі. Основна умова дроселювання (h 1 = h 2) визначає кінцевий стан пари перехрещенням горизонталі, які проходять через початкову точку, з ізобарою кінцевого тиску (рис. 9.10). З діаграми витікає, що температура водяної пари при дроселюванні зменшується (для водяної пари t кр = 374 ^оС, тому t інв = 4127 ^оС), при чому волога наcичена пара в залежності від початкового тиску, ступеня сухості і кінцевого тиску після дроселювання може бути вологою (a-b), сухою насиче ною (а-с) або навіть перегрітою (а-d), але з більш низьким тиском і температурою.

Рис. 9.10. Умовне зображення процесу дроселювання водяної пари на h – s -діаграмі

Слід звернути увагу на те, що при дроселюванні водяної пари питомий наявний теплоперепад (на рис. 9.10 характеризується відрізками 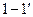до дроселювання і 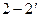після нього) зменшується, внаслідок чого працездатність потоку падає. Не дивлячись на те, що дроселювання є необоротним процесом і супроводжується втратою енергетичної цінності потоку, внаслідок простоти конструкції дросельних пристроїв вони широко застосовуються у техніці для регулювання і зміни витрати, а також отримання низьких температур і зрідження газів.

Дата добавления: 2014-01-07