Критерій Михайлова

Критерій Михайлова, як і критерій Гурвіца і Рауса, заснований на аналізі характеристичного рівняння системи, тому з його допомогою можна судити про стійкість замкнутих і розімкнених систем.

Ліва частина характеристичного рівняння називається характеристичним поліномом і має вигляд:

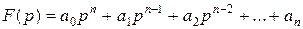
Підставивши в цей поліном замість змінної p чисто уявний корінь jw: p®jw отримаємо функцію комплексної змінної:

F(jw) = а₀(jw)ⁿ + а₁(jw)^n-1 + а₂(jw)^n-2 +…+ a_n.

Функцію F(jw) можна представити у вигляді суми дійсної і уявної частини: F(jw) = P(w)+jQ(w).

Дійсна частина P(w) містить тільки парні ступені w:

P(w) = a_n – a_n-2w² + a_n-4w⁴ - …

Уявна частина містить тільки непарні ступені:

Q(w) = a_n-1w – a_n-3w³ + …

Кожному значенню w відповідає комплексне число, яке може бути зображено у вигляді вектора на комплексній площині. Якщо тепер змінювати w від 0 до ¥, то кінець вектора F(jw) опише деяку криву, яка називається характеристичною кривою або годографом Міхайлова.

Критерій Міхайлова:

Автоматична система управління, що описується рівнянням n-го порядку, стійка, якщо при зміні w от 0 до ¥ характеристичний вектор системи F(jw) обернеться проти годинникової стрілки на кут 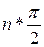, не звертаючись при цьому в нуль. Це означає, що характеристична крива стійкої системи винна при зміні w від 0 до ¥ пройти послідовно n чвертей.

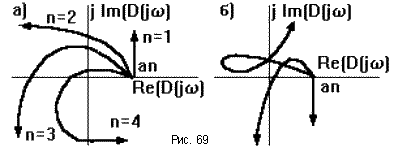
Крива F(jw) завжди починається в точці на дійсній осі, віддаленій в позитивному напрямі від початку координат на величину a_n. Характеристичні криві, що відповідають стійким системам, мають плавну спіралеподібну форму і йдуть в нескінченність в тій чверті, номер якої дорівнює порядку характеристичного рівняння. Якщо характеристична крива проходить n чвертей непослідовно, або проходить менше число чвертей, то система нестійка.

Якщо крива F(jw) проходить через початок координат, то система знаходиться на межі стійкості. Якщо F(jw)= 0 при w = 0 - аперіодична межа стійкості; якщо F(jw)= 0 при w ≠ 0 - коливальна межа.

Визначення типу межі стійкості по вигляду годографа Міхайлова

1. Астатизм першого порядку - "аперіодична" межа стійкості.

2. Астатизм другого порядку - "аперіодична" межа стійкості.

3. "Коливальна" межа стійкості.

4. Межа стійкості типу "нескінченний корінь".

Слідство з критерію Міхайлова:

Система стійка, якщо дійсна і уявна частини характеристичної функції F(jw) звертаються в нуль по черзі, тобто корені рівнянь Р(w) =0 і Q(w) =0 перемежаються.

Дата добавления: 2014-01-07