
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка качества дискретных систем
|
|
|
|
Качество дискретных систем управления характеризуется такими же показателями, как и качество непрерывных систем: точностью в установившихся режимах, длительностью и перерегулированием переходного процесса.
Длительность и перерегулирование оценивают непосредственно по переходной характеристике. Переходная характеристика дискретной системы строится гораздо проще, чем для непрерывной системы. Для этого записывают z-изображение выходной величины при единичном ступенчатом воздействии
 ,
,
а затем по изображению находят оригинал – решетчатую функцию x(iT).
В простых случаях функцию x(iT) можно найти при помощи таблиц обратного z-преобразования, разложив предварительно изображение X(z) на простые дроби.
В тех случаях, когда разложение на дроби связано с трудностями, целесообразно разложить функцию X(z) в степенной ряд по отрицательным степеням z (делением числителя на знаменатель):

Из определения z-преобразования вытекает, что коэффициенты степенного ряда по степеням z-1 представляют собой значения переходной характеристики h(t) в дискретные моменты времени t = iT (i = 1; 2; 3;…), т.е.
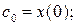

 …;
…;  …
…
Дискретные системы обладают специфической особенностью: переходные процессы в них могут заканчиваться за конечное число периодов Т, равное порядку системы n. Условием получения конечной длительности переходного процесса является равенство всех (кроме первого) коэффициентов характеристического уравнения замкнутой системы  нулю:
нулю: 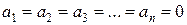 .
.
При этом характеристический полином системы имеет вид:
 ,
,
а изображение выходной величины оказывается конечным рядом отрицательных степеней z:
 ,
,
что соответствует переходному процессу с конечной длительностью 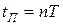 .
.
При любом другом соотношении коэффициентов длительность переходного процесса больше 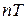 . Поэтому процесс с конечной длительностью будет оптимальным по быстродействию.
. Поэтому процесс с конечной длительностью будет оптимальным по быстродействию.
Точность дискретной системы оценивают по установившемуся значению сигнала ошибки:
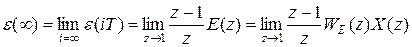 .
.
При ступенчатом воздействии 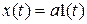 установившаяся ошибка:
установившаяся ошибка:
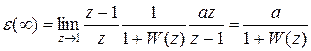 .
.
и называется статической ошибкой или ошибкой системы по положению.
При 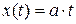 установившаяся ошибка называется ошибкой системы от скорости и определяется как
установившаяся ошибка называется ошибкой системы от скорости и определяется как

Если 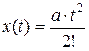 , то получаем ошибку системы от ускорения:
, то получаем ошибку системы от ускорения:
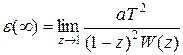
Из последних двух выражений следует, что установившаяся ошибка от задающего воздействия дискретных системы не только прямо пропорциональна величине задающего воздействия, но и периоду дискретности.
Дискретные системы классифицируются в соответствии с числом полюсов дискретной передаточной функции разомкнутой системы 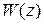 при
при  . Если дискретная передаточная функция дискретной разомкнутой системы
. Если дискретная передаточная функция дискретной разомкнутой системы
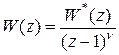
а 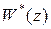 не содержит полюсов при
не содержит полюсов при  , то при
, то при  система называется статической, при
система называется статической, при  - астатической первого порядка и т.д.
- астатической первого порядка и т.д.
Для того чтобы дискретная система имела нулевую установившуюся ошибку от задающего воздействия, необходимо, чтобы степень астатизма 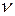 системы превышала степень полинома
системы превышала степень полинома  входного воздействия
входного воздействия 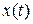 , то есть:
, то есть:
 , если
, если 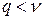 ;
;
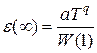 , если
, если  ;
;
 , если
, если  ;
;
Отсюда видно, что при ступенчатом воздействии ошибка будет равна нулю, если передаточная функция 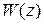 разомкнутого контура имеет хотя бы один полюс, равный единице. Аналогично можно показать, что при линейном воздействии ошибка равна нулю, если не менее двух полюсов равны единице.
разомкнутого контура имеет хотя бы один полюс, равный единице. Аналогично можно показать, что при линейном воздействии ошибка равна нулю, если не менее двух полюсов равны единице.
Коэффициенты ошибок. Если задающее воздействие 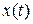 имеет произвольный вид, предельное значение ошибки вычисляется по формуле
имеет произвольный вид, предельное значение ошибки вычисляется по формуле
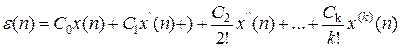 ,
,
где  ,
, 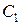 ,
, 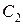 , - коэффициенты ошибок по положению, скорости, ускорению.
, - коэффициенты ошибок по положению, скорости, ускорению.
Коэффициенты ошибок находят по дискретной передаточной функции замкнутой импульсной системы по ошибке
 , для i = 0, 1, 2, …, k
, для i = 0, 1, 2, …, k
Число коэффициентов находится в соответствии с наибольшей степенью полинома входного воздействия.
В астатических системах несколько первых коэффициентов ошибок равны нулю: 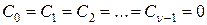 , где
, где 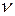 -порядок астатизма.
-порядок астатизма.
26. СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1400; Нарушение авторских прав?; Мы поможем в написании вашей работы!