Алгоритм розрахунку температури поверхні чипу ІМС процесора

Лекція №5

Для розрахунку температури поверхні чипу необхідно у визначеній загальній тепловій схемі (Рис. 5) знайти значення теплових опорів окремих теплових елементів. Далі шляхом еквівалентних перетворень схеми привести до виду:

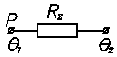
Де R_∑ - сумарний тепловий опір системи охолодження поверхні чипу;

θ₁ – температура поверхні чипу, яку необхідно визначити;

Р – потужність, яка виділяється на поверхні чипу.

На основі схеми Рис. 6. складаємо рівняння:

θ₁ – θ₂ = Р · R_∑, звідси

θ₁ = Р · R_∑ + θ₂

Виникає питання, від чого залежить потужність, що виділяється на поверхні чипу в сучасних цифрових ІМС. Відомо, що сучасні цифрові ІМС побудовані на основі комплементарних метало-окисел напівпровідникових (КМНО) структур, в яких основні витрати енергії визначаються витратами на перезарядку паразитних електричних ємностей, що визначаються елементами діелектричної ізоляції елементів самих структур.

Розглянемо крайній випадок. Електричну ємність визначимо площею чипу, наприклад S = 1 см², та товщиною діелектрика, наприклад d = 0,1 мкм, матеріал діелектрика SiO₂, ε ≈ 4, то:

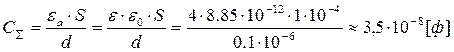
Тактова частота f_t = 2 ГГц = 2 · 10⁹ Гц;

Напруга переминання U = 1В.

Відомо, що енергія, яка необхідна на заряд конденсатора С від джерела постійного струму з напругою U складе CU²; причому половину цієї енергії CU²/2 витрачається на схемі заряду ємності, половина накопичується на конденсаторі, яка після витрачається на елементах електричної схеми при розряді конденсатора.

При наведених даних потужність Р, що буде виділятись на чипі наближено в крайньому випадку можна визначити:

Р = f_t ·CU² = 2·10^-9·3,5·10^-8 ≈ 70 Вт

Наведене показує, що енергії, пов’язаної з пере зарядом паразитних ємностей чипу суттєво залежить від рівня технології (проектно технологічних норм – товщини діелектрика), тактової частоти та розмірів чипу. І для швидкодіючих чипів вона складає не менше одиниці ват.

Визначення R_ч кондукцією від поверхні чипа до його основи.

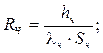
де h_ч – товщина;

S_ч – площа;

λ_ч – коефіцієнт теплопровідності матеріалу чипу (кремнію λ_Si = 150 [Вт/м°С]).

Приймаємо h_ч = 0,7 мм; S_ч = 1 см², тоді

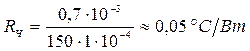
Визначення R_кр теплового опору кришки від зони її з’єднання з основою до протилежної поверхні:

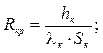
де h_к – товщина; S_ч – площа; λ_ч – коефіцієнт теплопровідності матеріалу кришки (корпусу).

Приймаємо h_к = 2 мм; S_ч = 25 см²; λ_к = 8 [Вт/м°С], матеріал 22ХС – кераміка на основі окислів Al₂O₃, тоді:

Визначення теплового опору шару R_ш між поверхнею кришки та поверхнею радіатора.

Тут можна розглядати різні варіанти передачі теплової енергії між поверхнями кришки та радіатора:

ü шар може бути у вигляді тонкого газового або рідинного прошарку, який забезпечує передачу тепла між поверхнями конвекцією;

ü шар може бути у вигляді тонкого прошарку теплопровідної пасти у вигляді гелю, який між поверхнями передає тепло кондукцією.

Для першого випадку тепловий опір конвекцією, нехтуючи товщиною шару і тепловим опором його кондукцією, тепловий опір можна визначити:

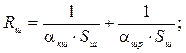
де S_ш – площа шару;

α_кш, α_кш – коефіцієнти тепловіддачі конвекцією кришка–шар (α_кш), та шар–радіатор (α_кш).

Враховуючи малу товщину шару, та високий при цьому градієнт температури в шарі, то можуть створюватися умови передачі теплової енергії від природних до примусових конвекцією як для газу, так і для рідини.

Тому коефіцієнти тепловіддачі α_кш і α_кш можуть знаходитися в діапазоні значень:

- для газового шару 2÷150 [Вт/м°С];

- для шару рідини 200÷3000 [Вт/м°С].

Якщо обмежимося можливими реальними значеннями для газового шару 30÷100 [Вт/м°С] та шару рідини 300÷1000 [Вт/м°С], то:

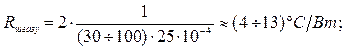
Наведені значення опорів R_{ш рід} та R_{ш газу} показують можливі реально значення R_ш коли має місце якісний тепловий контакт між радіатором і корпусом ІМС, або він втрачений в процесі експлуатації.

Тепловий опір радіатора R _р. Обмежимося тільки опором конвекцією між поверхнею радіатора та середовищем (опором кондукцією по матеріалу радіатора знехтуємо).

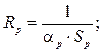
де S_р – площа поверхні радіатора, що віддає тепло;

α_р – коефіцієнти тепловіддачі.

Приймаємо α_р = 10÷100 Вт/м²·°С; S_р = 50÷300 см², тоді:

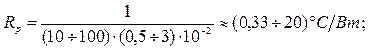
Визначення теплового опору основи R_ос від зони її з’єднання з кришкою до протилежної сторони (зони виводів):

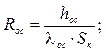
де h_ос – товщина; S_к – площа основи корпусу; λ_ос – коефіцієнт теплопровідності матеріалу основи корпусу.

Приймаємо h_ос = 2 мм; S_к = 25 см²; λ_ос = 8 Вт/м°С, тоді:

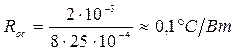
Тепловий опір виводів R_в:

де h_в – довжина; S_в – площа перетину; N_в – число виводів; λ_в – коефіцієнт теплопровідності матеріалу виводів.

Приймаємо N_в = 400 одиниць; h_в = 1 мм; S_в = 1 мм²; λ_в = 120 Вт/м°С, тоді:

Тепловий опір ділянки контактної зони друкованої плати R_{дп 11} кондукцією з однією на протилежну її сторону:

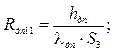
де h_дп – довжина; S_з – площа зони контактів друкованої плати; λ_дп – коефіцієнт теплопровідності плати.

Приймаємо h_дп = 3 мм; S_з = 25 см²; λ_дп = 10 Вт/м°С, тоді:

Тепловий опір конвекцією контактної зони друкованої плати R_{дп 12}:

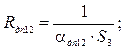
де α_{дп 12} – коефіцієнти тепловіддачі ділянки контактної зони друкованої плати;

S_з – площа зони;

Приймаємо α_{дп 12} = 5 Вт/м²°С, тоді:

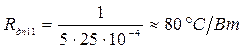
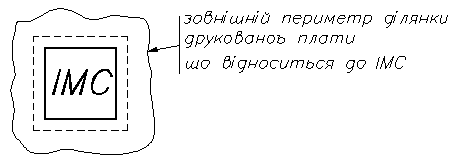
Тепловий опір кондукцією ділянки друкованої плати R_{дп 21} від зони контактів до зовнішнього периметру ділянки друкованої плати, який відноситься до ІМС.

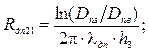
де D_пв – ефективний діаметр зони контактів;

D_пз – ефективний діаметр ділянки плати ІМС.

D_пз = ,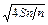

де S_n – площа плати, що відноситься до ІМС.

Приймаємо D_пв / D_пв = 2, тоді:

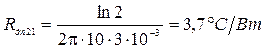
Тепловий опір ділянки друкованої плати конвекцією за межами ділянки контактної зони:

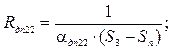
де α_{дп 22} – коефіцієнти тепловіддачі ділянки за межами контактної зони;

S_п – площа ділянки друкованої плати, що відноситься до ІМС.

Приймаємо α_{дп 22} = 10÷100 Вт/м²·°С; S_п = 100 см², тоді:

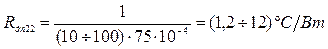
Приведемо еквівалентну схему з визначеними величинами теплових опорів.

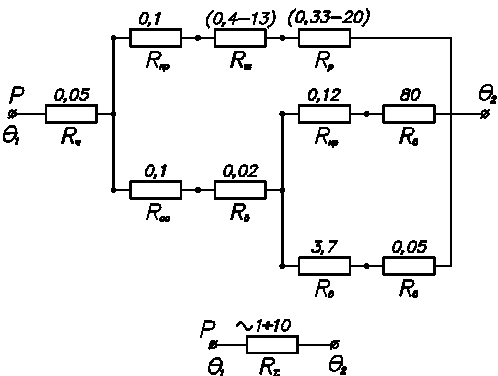
θ₁ = θ₂ + Р · R_∑ = 20 + (10 ÷ 100) = 30 ÷ 120 °С

Дата добавления: 2014-01-07