Тема 1. Стабілізація неперервних технологічних процесів

Вплив таких властивостей технологічних процесів як розподільність змі-нних, запізнення, нестаціонарність, нелінійність, наявність самовирівнювання на структуру автоматичних систем регулювання (АСР). Застосування замкне-них та розімкнених АСР.

Види комбінованих АСР. Використання принципа інваріантності при їх по-будові. Фізична реалізація та настройка комбінованих АСР. Види каскадних АСР.

Загальна характеристика методів настройки регуляторів. Аналітичні і експериментальні методи настройки регулятора. Настройка за характерис-тиками об’єкта та системи. Методи реалізації настройк.

Визначемо вплив показників статичних і динамічних характеристик об'єкта за різними каналами на такі найважливіші показники якості процесу регулю-вання, як динамічна і статична помилки. Структура найпоширенішої однокон-турної замкнутої АСР (рис.1) включає в себе об'єкт керування (ОК) і автома-тичний регулятор (АР). На рис.1 застосовані такі позначення: X*(p), X(р) – зображення за Лапласом відповідно змін завдання і регульованої змінної; U(p), Z(р) – зображення за Лапласом відповідно змін керувальної дії і збурення; W_ОК(р), W_ОЗ(р) – передатні функції об'єкта за каналами керування й збурення. Як відомо з теорії автоматичного керування, для замкнутої системи стабілізації справедливим є таке співвідношення, що зв'язує відхилення регульованої змі-нної Х(р) зі зміною збурення

Х(р) = Z(p) W_ОЗ(р) / [1+ W_ОК(р) W_Р(р)]. (1)

Для систем програмного регулювання і слідкування взаємозв'язок зміни X (p) із зміною завдання Х*(p) має такий вигляд:

Х(р)= Х*(p) W_ОК(р) W_Р(р)] / [1+ W_ОЗ(р) W_Р(р)]. (2)

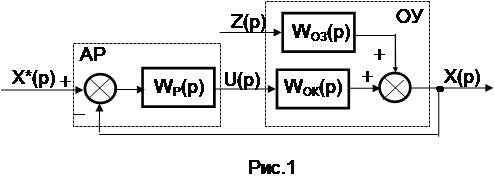Із співвідношень (1) і (2) видно, що менші відхилення X будуть спостеріга-тися в об'єктах із меншими передатними функціями за каналами збурення і великими – за каналами керування.

У статиці (р = 0) передатні функції вироджуються у відповідні коефіцієнти передачі. Для вибору каналу регулювальної дії визначають вплив вхідної дії за розміром коефіцієнта передачі об'єкта за каналом керування K_К і діапазоном зміни керувальної дії Du_mах. Домогтися необхідної якості регулювання в статиці можна, якщо вплив керувальної дії на регульовану змінну не буде меншим впливу найбільшого із збурень, тобто при виконанні умови:

|K_К Du_mах | ³ | K_З Dz_mах |, (3)

де K_З – коефіцієнт передачі за каналом збурення.

Під час аналізу динамічних властивостей об'єктів у першу чергу необхідно враховувати місце вводу керування і збурення (у багатоємнісних об'єктів вони різні). У переважній більшості випадків передатні функції об'єкта за каналами збурення і керування апроксимуються залежностями вигляду

W_ОЗ(р) = K_З ехр(– рt_З) / (Т_З р +1), (4)

W_ОК(р) = K_К ехр(– рt_К) / (Т_К р +1), (5)

де Т_З,Т_К – сталі часу за каналами збурення і керування; t_З, t_К – запізнення за цими самими каналами. Спільний аналіз виразів (1), (4) і (5) показує, що менша динамічна помилка буде (при тому самому збуренні) в об'єкті, у якого більша Т_З і менше Т_К і t_К.

Якщоза допомогою замкнутої одноконтурної системине забезпечується необхідна динамічна помилка, тозастосовуютьсябагатоконтурні АСР, най-більш поширеними серед яких є комбіновані.Вонивикористовуютьсяу випа-дках, коли об’єкт має несприятлеві динамічні властивості за каналом збурення (найчастіше – основного) і є вимірювальні перетворювачі для його виміру. При побудові комбінованої АСР необхідно розробити її структуру і визначити па-раметри компенсатора (компенсаторів). Передатна функція компенсатора виз-начається передатними функціями об'єкта за каналами основного збурення і керування. Вихід компенсатора може бути під’єднаний безпосередньо до входу об'єкта (до виконавчого механізму, на який впливає регулятор) (рис.2, 1-ий варіант) або до входу регулятора (рис. 2, 2-ий варіант). При під’єднанні ком-пенсатора до входу об'єкта передатна функція компенсатора W_K(p) визначає-ться за співвідношенням

W_K(p) = W_OЗ (p) / W_OК (p), (6)

а у разі під’єднанні компенсатора до входу регулятора – за співвідношенням

W_K(p) = W_OЗ (p) / W_Р (р) × W_OК (p), (7)

де W_Р (p) – передатна функція регулятора.

В обох випадках буде забезпечуватися часткова інваріантність АСР (інва-ріантність щодо основного збурення, яке компенсується), що дасть можливість зменшити динамічну помилку регулювання. Проте порівняння обох варіантів показує, що кращим є під’єднання компенсатора до входу об'єкта. При цьому структура компенсатора залежить тільки від властивостей об'єкта. При під’єд-нанні до входу регулятора, як випливає з виразу (7) зміна настройки регуля-тора, потребує зміни настройки компенсатора, а зміна закону регулювання ре-гулятора спричинить необхідність заміни компенсатора. Крім того, у цьому разі можливе також виникнення статичної помилки, зумовлене тим, що на вході регулятора будуть зрівнюватися не тільки сигнали завдання X* і поточного значення змінної X, але й і сигнал компенсатора.

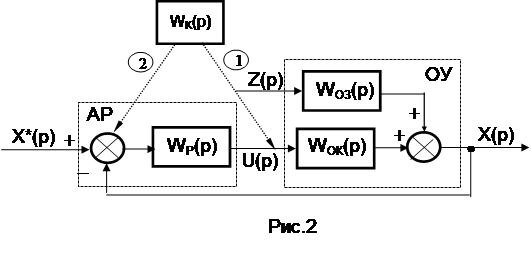
Отже, така АСР повинна забезпечити виконання таких умови в статиці:

Х* = Х + Z K_K, (8)

де K_K - коефіцієнт передачі компенсатора.

Якщо комбіновані АСР ефективні при неприятливих динамічних власти-востях об’єкта за каналом збурення, то при несприятлевих динамічних власти-востях об’єкта за каналом регулювальної дії більш ефективні каскадні систе-ми, які складаються з внутрішнього і зовнішнього контурів регулювання. Іс-нують чотири класи таких систем: каскадно-зв’язані, каскадно-диференціальні, каскадно-автономні і каскадно-незв’язані.

Каскадно-зв’язані як і більшість інших каскадних систем мають два контури регулювання, які розташовані один в другому: головний РГ (зовнішній, коригувальний або задавальний) та допоміжний РД (внутрішній, стабілізуючий або слідкувальний). Основна регулювальна величина об’єкта подається на вхід РГ, а сигнал проміжної змінної на вхід РД. Вихід РГ використовується для зміни завдання РД, який в свою чергу діє на регулювальний орган

Структурна схема системи наведена на рис.3. Формула, що ій відподає має такий вид:

Х(р) = X*(p)W_CГ(р)/[1+W_CГ(р)+W_CВ(р)]+Z₁(p)W_ОЗ1(p)W_ОК2(p)/[1+W_CГ(р) +

+ W_CВ(р)] + Z₂(p)W_ОЗ2(p)[1+ W_CВ(р)]/[1+ W_CГ(р)+ W_CВ(р)], (9)

де W_CГ(р) = W_РГ(р)W_РВ(р)W_ОК1(p)W_ОК2(p); W_CВ(р) = W_РВ(р)W_ОК1(p) – передатні функції відповідно розімкнутих систем головного і допоміжного регуляторів.

Із структурної схеми видно, що внутрішній контур послаблює дію збурень, які охоплює цей контур на регульовану величину Х(р), причому ця дія буде тим менше, чим більша швидкодія допоміжного контуру порівняно з головним контуром. Це накладає певні вимоги га вибір допоміжної змінної Х_П(р), яка повинна зі значно меншою інерційністю порівняно з Х(р) реагувати на основні збурення.

Таким чином, застосування каскадних АСР доцільно в тих випадках, коли внутрішній контур має значно більшу швидкодію ніж зовнішній і коли основні збурення охоплені внутрішнім контуром. До таких збурень відносяться часті зміни якості регулювального середовища з умовою, що динамічні властивості об’єкта за цим каналом гірші ніж за каналами інших збурень. Інший випадок застосування каскадних АСР пов’язаний з паралельною роботою групи апара-тів. Тоді кількість внутрішніх контурів дорівнює кількості апаратів, причому кожний з цих контурів стабілізує технологічний режим в певному апараті, а РГ діє на них, змінюючи завдання РД у разі необхідності зміни режиму роботи такого технологічного комплексу. Зменшення впливу цих збурень на Х(р) мо-жна досягнути і за рахунок додаткових автономних регуляторів стабілізації цих збурень, але в такому випадку необхідне застосування додаткових регулю-вальних органів.

Вважають, що динамічна похибка каскадної АСР по відношенню збурень, що охоплені внутрішнім контуром, зменшується у 10-100 разів, а по відноше-нню збурень, що не охоплені цим контуром у 2-5 раз, порівняно із застосу-ванням одно контурних АСР. Останнє відбувається за рахунок зменшення інерційності системи.

До об’єктів, що потребують каскадних АСР, відносяться, насамперед, підігрівачі, у яких теплоносій і продукт розділені по верхньою нагріву. В цьому випадку за каналом регулювальної дії цей об’єкт є багатоємнісним, а за ка-налом основного збурення (витрати продукту) – одно ємнісним. Тому для пок-ращення якості регулювання температури продукту використовують проміжну змінну – температуру теплоносія біля поверхні нагріву.

До цього розглянуті об’єкти з однією регульованою зміною, тобто одно-вимірні, але більшість об’єктів є багатовимірними, тому що мають регульо-ваних змінних. При цьому у багатовимірних багато зв’язаних об’єктах між вхід-ними і вихідними змінними існують перехресні зв'язки. За відсутності пере-хресних зв'язків, коли кожна керуюча дія впливає лише на одну вихідну змінну, об'єкт можна розглядати як сукупність одновимірних (однозв'язаних) об’єктів, для регулювання яких використовують розглянуті раніше одно- і багато- контурні АСР однієї змінної.

Якісну оцінку взаємного впливу двох контурів регулювання проводять за допомогою комплексного коефіцієнта зв’язності:

К_ЗВ(jw) = W₁₂(jw) W₂₁(jw) / W₁₁(jw) W₂₂(jw), (10)

де W₁₂(jw), W₂₁(jw) – частотні характеристики об'єкта за перехресними канала-ми: u₁–x₂,u₂–x₁; W₁₁(jw), W₂₂(jw) – частотні характеристики об'єкта за прямими каналами: u₁–x₁, u₂-–₂ (рис.4).

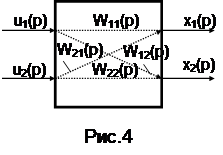Значення коефіцієнта зв’язності зазвичай визначають при w = 0 (у статиці) і робочих частотах обох контурів регулювання. Зокрема K_ЗВ(0) визначається відношенням коефіцієнтів передачі за перехресним і основним каналами. За значенням цього коефіцієнта виділяють 4 випадки:

1) K_ЗВ 0, об'єкт розглядають як одноз’вязаний і застосовують незв'язане регулювання окремих змінних за допомогою одно- або багатоконтурних АСР;

2) K_ЗВ>1, міняють місцями прямі і перехресні канали;

3) 1>K_ЗВ>0, застосовують зв'язане регулювання із використанням автоно-мних багатоконтурних систем регулювання;

4) K_ЗВ=1, найскладнішим випадок, тому що інерційності прямих і пере-хресних каналів однакові, запас стійкості за модулем зменшується в 2 рази, а застосування автономного регулювання не дає бажаного ефекта, тому застосо-вують незв’язане регулювання.

Автономні системи регулювання дають можливість проводити незале-жне регулювання взаємозалежних змінних. Вони включають, крім основних регуляторів, додаткові динамічні компенсатори. Умова автономності двох регу-ляторів (рис.5) складається з двох умов інваріантності: інваріантності першого виходу х₁ щодо керувальної дії u₂ іншого регулятора й інваріантності другого виходу х₂ щодо сиг-налу u₁ першого регулятора:

х₁ (t, u₂) = 0, х₂ (t, u₁) = 0. (11)

При цьому вплив u₁ можна розглядати як збурення для х₂, а вплив u₂ – як збурення для х₁. Отже, перехресні канали відіграють роль каналів збурення, тоді:

W_1К(р) = W₁₂(р)/W₂₂(р); W_2К(р) = W₂₁(р)/W₁₁(р). (12)

Недоліками автономних АСР є складність їх розрахунку і налагодження; великі витрати на створення автономної АСР з великою кількістю перехресних зв'я-зків; при n перехресних зв'язків потрібно n(n-1) компенсаторів.

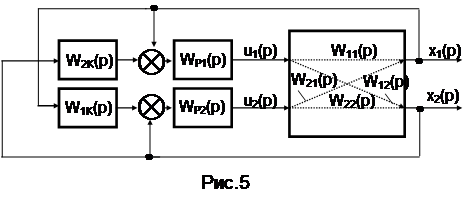При цьому вплив u₁ можна розглядати як збурення для х₂, а вплив u₂ – як збурення для х₁. Отже, перехресні канали відіграють роль каналів збурення, тоді:

W_1К(р) = W₁₂(р)/W₂₂(р); W_2К(р) = W₂₁(р)/W₁₁(р). (13)

Недоліками автономних АСР є складність їх розрахунку і налагодження; великі витрати на створення автономної АСР з великою кількістю перехресних зв'я-зків; при n перехресних зв'язків потрібно n(n-1) компенсаторів.

При створенні АСР необхідно не тільки розробити структуру системи та ви-значити передатні функції її компонентів, але й виконати її параметричну оптимізм-цію, тобто визначити оптимальні настройки регулятора. При цьому параметри настройки регулятора повинні бути такими, щоб у замкненої АСР обраний показник якості регулювання прагнув до екстремального значення при обмеженні за стійкістю системи. Для АСР з лінійними регуляторами як крите-рій використовують один із таких показників: час регулювання, динамічна по-хибка, інтегральні критерії якості, середня квадратична похибка. При оптимі-зації прагнуть їх мінімізувати. Обмеженням при цьому найчастіше виступає ступінь згасання перехідного процесу y або ступінь коливальності m. Опти-мізація в інженерній практиці проводиться як аналітичними, так і експери-ментальними методами. Серед яких доволі поширеним є метод Циглера – Ніко-льса, призначений для визначення настройок регуляторів, що забезпечують мінімум інтегрального квадратичного критерію при ступені згасання не нижче 0,8. Відповідно до цього методу розрахунок настройок виконують у два етапи:

1) розраховують критичну настройку АСР з П-регулятором, за якою система перебуватиме на межі стійкості;

2) визначають за значеннями критичного коефіцієнта передачі регулятора К_Р.КР і частоти власних коливань w_КР оптимальні настройки регулятора.

Існує також група експериментальних методів, які базуються на засто-суванні наближеної моделі об’єкта чи системи, отриманої з використанням не-великої кількості типових елементарних ланок. Послідовність настроювання за цими методами при використанні моделі об’єкта така:

1) вибирають критерій оптимальності перехідного процесу (КОПП) АСР;

2) визначають динамічні параметри об’єкта (ДПО) з використанням, як правило, експериментальних методів з аперіодичними, періодичними або випа-дковими вхідними діями;

3) з допомогою номограм або спрощених формул для обраного КОПП та визначених ДПО розраховують оптимальні параметри настроювання регуля-тора;

4) реалізують розраховані настройки на регуляторах контролерів програм-ним шляхом; для подолання розбіжності між якісними показниками перехід-ного процесу і КОПП, що виникають у результаті прийнятих спрощень, настро-йки регулятора уточнюють під час спробної експлуатації АСР.

А при використанні моделі системи (1 п. такий же):

2) замкнену чи розімкнену АСР досліджують з періодичними, аперіодич-них чи випадковими збуреннями;

3) далі при застосуванні ітераційного пошукового алгоритму покроково змінюють параметри настройки регулятора (ПНР) до досягнення екстремаль-ного значення КОПП.

Література для самостійної роботи: [5] С.19,20,26-41,51-57; [1] С.3-5,6,7, 9-11, 13,14,16-19,22-27; [9] С.327-341; [10] с.817-819, 861-885, 892- 895, 901-910; [17] с.279-301; [3] с. 82-87, 99-119.

Дата добавления: 2014-01-07