
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон Дальтона
|
|
|
|
Якщо в об’ємі знаходиться суміш з N газів, що хімічно не взаємодіють, то тиск суміші визначається за законом Дальтона – тиск суміші газів дорівнює сумі парціальних тисків кожного газу, що складає суміш:
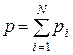 . (1.11)
. (1.11)
Парціальний тиск 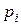 – це тиск, що створює складовий газ суміші, якби тільки цей газ один займав увесь об’єм, в якому знаходиться суміш.
– це тиск, що створює складовий газ суміші, якби тільки цей газ один займав увесь об’єм, в якому знаходиться суміш.
Дійсно, якщо визначити в одиницях pV масу суміші газу як суму мас окремих газів, що складають суміш, то матимемо
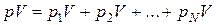 ,
,
після скорочення подібних отримаємо (1.11).
Запитання для самоперевірки
1. У чому полягають електричні вимірювання температури?
2. Дайте визначення критичної температури тіла.
3. Сформулюйте і запишіть закон Бойля – Маріотта.
4. Сформулюйте і запишіть закон Гей – Люссака.
5. Сформулюйте і запишіть об’єднаний газовий закон Менделеева – Клапейрона.
6. Сформулюйте і запишіть закон Авогадро.
7. Дайте визначення парціального тиску.
8. Сформулюйте і запишіть закон Дальтона.
Лекція друга
МОЛЕКУЛЯРНО – КІНЕТИЧНА ТЕОРІЯ ГАЗІВ
2.1. Елементи молекулярно – кінетичної теорії газів. Основне рівняння молекулярно – кінетичної теорії
Хоча будь-який газ виявляє себе завдяки тиску, закони ідеальних газів не дають можливості відповісти, що таке тиск газу і чим він викликається. На ці запитання допомагає відповісти молекулярно-кінетична теорія газів, яка будується на таких допущеннях:
1) газ – це сукупність окремих молекул, які знаходяться в безперервному і хаотичному русі;
2) взаємодіють молекули одна з одною тільки в результаті зіткнень, а тому траєкторія їх руху - це ламана лінія;
3) молекули наскільки малі, що їх можна вважати матеріальними точками;
4) газ є ізотропним середовищем, тобто в ньому немає будь-яких переважних напрямків.
За основним рівнянням молекулярно-кінетичної теорії газів
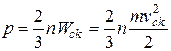 , (2.1)
, (2.1)
де n – концентрація молекул, тобто число молекул в одиниці об’єму; m – маса одній молекули газа; v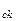 – середня квадратична швидкість молекули; W
– середня квадратична швидкість молекули; W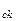 – середня квадратична енергія поступового руху одної молекули.
– середня квадратична енергія поступового руху одної молекули.
Таким чином можна сказати, що тиск, за яким визначають наявність газу в будь-якому об’ємі - це середня сила, з якою молекули газа діють на одиницю площі стінки ємності, де він знаходиться.
З молекулярно-кінетичної теорії газів відомо, що молекули мають багато ступенів свободи руху і на одну ступінь поступового руху припадає енергія, яка дорівнює kT/2. Тому повна середньоквадратична енергія поступового руху одної молекули
W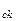
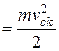
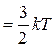 , (2.2)
, (2.2)
де k – постійна Больцмана (k = 1, 38
= 1, 38 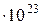 Дж/К).
Дж/К).
2.2. Рівняння Больцмана
Враховуючи вирази (2.1) і (2.2), отримаємо рівняння Больцмана, яке фактично в іншій формі виражає об’єднаний газовий закон, але вже на основі молекулярно-кінетичної теорії:
p= nkT. (2.3)
Наслідком рівняння Больцмана є висновок, що молекулярна концентрація не залежить від природи газу
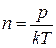 , (2.4)
, (2.4)
а також можливість отримати співвідношення між густиною газу, його тиском і температурою
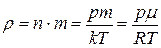 . (2.5)
. (2.5)
2.3. Дослід Кантора
 Якщо в колбі з водяною парою (рис.2.1) розмістити рухому слюдяну пластинку 1, яка з одного боку покрита порошком фосфорного ангідриду 2, то пластинка відхилиться від вертикального положення, наче на неї діє з непокритого боку - якась сила. Дійсно, від слюди молекули водяної пари будуть пружно відлітати, тоді як на покритому боці вони будуть поглинатися ангідридом в результаті хімічного реагування.
Якщо в колбі з водяною парою (рис.2.1) розмістити рухому слюдяну пластинку 1, яка з одного боку покрита порошком фосфорного ангідриду 2, то пластинка відхилиться від вертикального положення, наче на неї діє з непокритого боку - якась сила. Дійсно, від слюди молекули водяної пари будуть пружно відлітати, тоді як на покритому боці вони будуть поглинатися ангідридом в результаті хімічного реагування.
|
2.4. Барометрична формула
Якщо молекули газа знаходяться під дією сили тяжіння (або будь-якої центральної сили), то незважаючи на їх хаотичний рух вони не розлітаються у просторі, а утворюють газову оболонку (наприклад атмосферу Землі). У цьому випадку тиск газу змінюється залежно від висоти h над Землею.
За теоремою Паскаля при збільшенні висоти на величину dh тиск зменшиться на
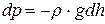 . (2.6)
. (2.6)
Оскільки густина газу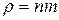 , а концентрацію
, а концентрацію 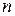 виразимо за рівнянням Больцмана, то можна скласти диференціальне рівняння
виразимо за рівнянням Больцмана, то можна скласти диференціальне рівняння
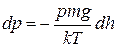 . (2.7)
. (2.7)
Після відокремлення змінних величин і проведення інтегрування, при припущенні, що сила земного тяготіння не змінюється, отримаємо залежність тиску газу від висоти над Землею:
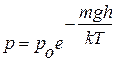 , (2.8)
, (2.8)
яка і називається барометричним рівнянням Больцмана; p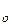 – тиск газу на поверхні Землі (над рівнем моря; h = 0).
– тиск газу на поверхні Землі (над рівнем моря; h = 0).
Якщо тиск виразити через концентрацію молекул газа і взяти до уваги, що 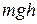 – це потенціальна енергія W молекул на висоті h, то з барометричної формули (2.8) одержимо залежність, що показує як змінюється концентрація молекул газа, коли вони знаходяться в будь-якому потенціальному полі:
– це потенціальна енергія W молекул на висоті h, то з барометричної формули (2.8) одержимо залежність, що показує як змінюється концентрація молекул газа, коли вони знаходяться в будь-якому потенціальному полі:
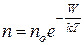 , (2.9)
, (2.9)
де n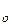 – концентрація молекул газу на поверхні Землі.
– концентрація молекул газу на поверхні Землі.
Оскільки рівняння (2.8) і (2.9) справедливі для будь-якого силового поля і не тільки для молекул газа, а й інших частинок, що рухаються хаотично, то його називають законом Больцмана або законом розподілу частинок, що знаходяться під дією силового поля.
2.5. Максвеллівський розподіл швидкостей молекул газу
Одним з положень молекулярно-кінетичної теорії є припущення, що молекули, з яких складається газ, рухаються хаотично і місцезнаходження будь-якої молекули має випадковий характер. Окрім цього молекули нічим не відрізняються одна від одної і їх дуже багато (наприклад в 1см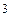 повітря за нормальних умов, знаходиться приблизно 10
повітря за нормальних умов, знаходиться приблизно 10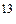 молекул). Усі ці положення стверджуються в досліді з броунівського руху. У зв’язку з цим важливими параметрами, що характеризують газ, будуть середні величини, тобто величини, що характеризують не одну окрему молекулу, а всі молекули одночасно в заданому об’ємі.
молекул). Усі ці положення стверджуються в досліді з броунівського руху. У зв’язку з цим важливими параметрами, що характеризують газ, будуть середні величини, тобто величини, що характеризують не одну окрему молекулу, а всі молекули одночасно в заданому об’ємі.
Для визначення і розрахунку середніх величин, що характеризують великий ансамбль одиниць, для яких наведені положення задовольнюються, використовуються методи статистичних досліджень, тобто науки статистики. Статистика оперує такими величинами, як імовірність, флуктуація, функція статистичного розподілу, середні значення, то саме такими величинами і можна буде характеризувати газ.
Будемо вважати, що всі напрями в газі рівноймовірні і тому молекули можуть мати швидкість v, що не залежить від напряму. Взаємодіють молекули тільки в результаті пружних зіткнень, а тому матимуть найрізніші швидкості як за напрямом, так і за величиною. Наше завдання полягає в тому, щоб знайти закон, за яким будуть розподілятися швидкості молекул газа.
Позначимо в декартовій системі координат число молекул, швидкості яких в напрямі осі x лежать в межах від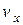 до
до 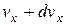 , як
, як 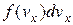 . Це буде означати, що імовірність наявності у молекули швидкості
. Це буде означати, що імовірність наявності у молекули швидкості 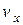 дорівнює
дорівнює 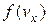 . Оскільки всі напрями рівноймовірні, то аналогічно в напрямі осей y і z число молекул, швидкості яких лежать в межах від
. Оскільки всі напрями рівноймовірні, то аналогічно в напрямі осей y і z число молекул, швидкості яких лежать в межах від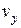 до
до 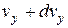 і від
і від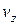 до
до 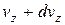 , буде
, буде 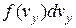 і
і 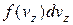 відповідно. Таким чином, загальна кількість молекул, що в будь-який момент мають швидкості
відповідно. Таким чином, загальна кількість молекул, що в будь-який момент мають швидкості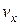 ,
, 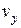 і
і 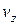 , буде дорівнюватиме добутку
, буде дорівнюватиме добутку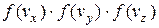
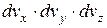 і це означає, що вона залежить не від напряму, а тільки від величини швидкості.
і це означає, що вона залежить не від напряму, а тільки від величини швидкості.
Якщо введемо результуючу швидкість як  , то тоді добуток
, то тоді добуток 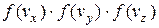 можна виразити однією функцією, яка залежить тільки від
можна виразити однією функцією, яка залежить тільки від 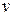 :
:
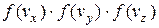 =
=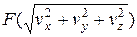 =
=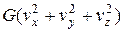 . (2.10)
. (2.10)
Єдиним рішенням цього рівняння буде функція
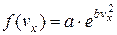 ,
, 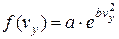 ,
, 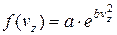 .
.
Стала величина а є додатною, оскільки імовірність не може бути від’ємною. Тоді можна записати
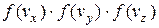 =
=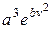 .
.
Будемо вважати, що при відповідних умовах в газі є загальна кількість молекул N. Тоді частина молекул від N, які мають швидкості в межах від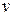 до
до 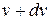 , дорівнюватиме
, дорівнюватиме
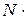
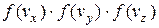
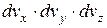 =
=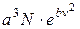
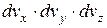
і в просторі швидкостей в декартових координатах це можна показати, як на рис. 2.2, де певна частина молекул буде знаходитися у середині вказаного куба.
|
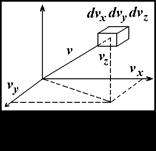 Оскільки всі напрями швидкостей рівноймовірні, то будуть ще молекули з таким ж швидкостями за величиною, але направлені за всіма напрямами. Щоб визначити загальне число молекул з такими швидкостями, необхідно підрахувати скільки молекул буде в кульовому шарі радіусом
Оскільки всі напрями швидкостей рівноймовірні, то будуть ще молекули з таким ж швидкостями за величиною, але направлені за всіма напрямами. Щоб визначити загальне число молекул з такими швидкостями, необхідно підрахувати скільки молекул буде в кульовому шарі радіусом 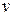 і товщиною
і товщиною  . Відомо, що об’єм такого шару дорівнює
. Відомо, що об’єм такого шару дорівнює 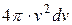 , тоді можна записати, що частина молекул
, тоді можна записати, що частина молекул 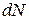 зі швидкостями від
зі швидкостями від 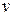 до
до 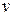 +
+ дорівнюватиме
дорівнюватиме
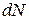
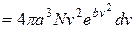 (2.11)
(2.11)
а загальне число всіх молекул N з допущенням, що вони мають швидкості від 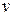 =0 до
=0 до 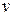 =
=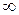 , буде
, буде
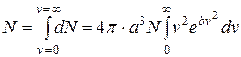 . (2.12)
. (2.12)
Загальне число молекул газа можна визначити незалежно від цього, тоді з рівняння (2.12) знайдемо сталі а і b. Дійсно, інтеграл в (2.12) буде скінченним тільки за умови, що значення сталої b є від’ємним. Таким чином b< 0. Окрім цього, показник експоненти повинен бути безрозмірним, а тому розмірність b має бути оберненою до 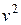 і можна допустити, що b
і можна допустити, що b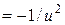 , де
, де 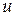 – якась величина з розмірністю швидкості, до того ж однакова для всіх молекул визначеного газу, але залежна від температури, що характеризує стан цього газу.
– якась величина з розмірністю швидкості, до того ж однакова для всіх молекул визначеного газу, але залежна від температури, що характеризує стан цього газу.
Після проведення інтегрування в (2.12) при врахуванні, що
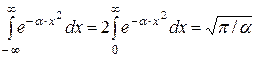 , (2.13)
, (2.13)
а також, що після диференціювання інтеграла в (2.13) за параметром  –
–
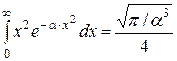 ,
,
отримаємо
1=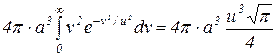
і визначимо сталу, тобто 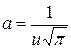 .
.
Підставляючи визначені сталі в (2.11), отримаємо
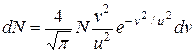 . (2.14)
. (2.14)
Це рівняння називають максвелловським розподілом швидкостей газу у відповідному стані за визначеними значеннями u і N. Графік цього розподілу має такий вигляд, як на рис.2.3.
2.5.1. Швидкості молекул газу
З графіка функціі видно, що вона має максимум при 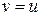 , тобто швидкість
, тобто швидкість 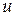 молекули мають частіше, ніж іншого значення і з цієї причини її називають найбільш ймовірною. Наприклад, швидкість, що вдвічі більша за найбільш ймовірну зустрічається приблизно в 0,2 рази рідше, ніж найбільш ймовірна. Величина найбільш ймовірної швидкості залежить від температури і природи газу
молекули мають частіше, ніж іншого значення і з цієї причини її називають найбільш ймовірною. Наприклад, швидкість, що вдвічі більша за найбільш ймовірну зустрічається приблизно в 0,2 рази рідше, ніж найбільш ймовірна. Величина найбільш ймовірної швидкості залежить від температури і природи газу
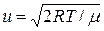 =
=  . (2.15)
. (2.15)
Середня квадратична швидкість молекул знаходиться за формулою
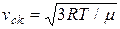 =
= 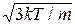 , (2.16)
, (2.16)
|
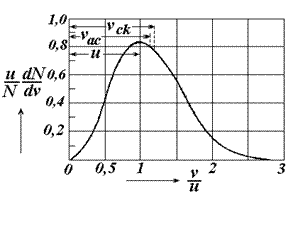
Рис. 2.3
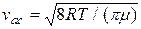 =
= 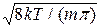 . (2.17)
. (2.17)
Якщо вираз для найбільш ймовірної швидкості (2.15) підставимо в рівняння (2.14), то отримаємо в іншому вигляді функцію розподілу молекул за швидкостями, яка ще називається функцією Максвелла – Больцмана:
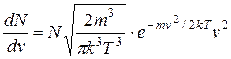 . (2.18)
. (2.18)
При врахуванні, що кінетична енергія молекули це –
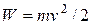 ,
,
отримаємо з (2.18) рівняння розподілу кінетичної енергії молекул:
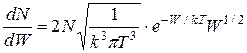 . (2.19)
. (2.19)
Запитання для самоперевірки
1. Сформулюйте основні положення молекулярно-кінетичної теорії газів?
2. Що таке тиск згідно з молекулярно-кінетичною теорією газів?
3. Сформулюйте і запишіть рівняння Больцмана і наслідки, що випливають з нього.
4. Що показує дослід Кантора?
5. Поясніть, що відображає барометричне рівняння Больцмана.
6. Як змінюється концентрація газу, що знаходиться під дією центральної сили?
7. При яких умовах максвеллівський розподіл швидкостей молекул справедливий?
8. Який вигляд має максвеллівський розподіл швидкостей молекул і що він показує?
9. Запишіть як виражається середня квадратична швидкість молекул газу.
10. Дайте визначення найбільш ймовірної швидкості молекул газу.
Лекція третя
ЧИСЛО МОЛЕКУЛ, ЩО УДАРЯЮТЬСЯ В СТІНКУ.
ТЕЧІЯ ГАЗУ ЧЕРЕЗ ОТВІР У ТОНКІЙ СТІНЦІ. ЗАКОН ГРЕХЕМА
3. 1. Число молекул, що ударяються в стінку
У вакуумній техніці в багатьох випадках необхідно визначити кількість молекул газу, що проникнуть за одиницю часу через якийсь отвір у стінці ємності, в якій знаходиться газ. Для цього необхідно знати кількість молекул газу, що ударяються за одиницю часу в одиницю площини стінки ємності, в якій знаходиться газ.
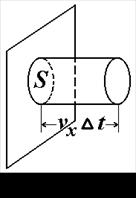 Розглянемо циліндр з площею основи S і довжиною
Розглянемо циліндр з площею основи S і довжиною 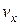
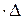 t, що дорівнює відстані, яку пробігає одна молекула за проміжок часу
t, що дорівнює відстані, яку пробігає одна молекула за проміжок часу 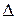 t, маючи на увазі, що вона ударяється в стінку (основу S). Тоді число молекул, що ударяється в основу S дорівнюватиме
t, маючи на увазі, що вона ударяється в стінку (основу S). Тоді число молекул, що ударяється в основу S дорівнюватиме
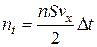 .
.
|
Оскільки 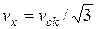 , то за одиницю часу
, то за одиницю часу
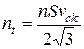
Замінимо середню квадратичну швидкість на середню арифметичну, тоді отримаємо
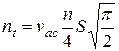 .
.
Якщо враховувати, що не всі молекули спрямляються до основи перпендикулярно, а частина буде ударятися під всілякими кутами, то необхідно підкореневий вираз замінити на одиницю і остаточно отримаємо число молекул газу, що ударяються за одиницю часу в одиницю площини стінки
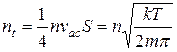 . (3.1)
. (3.1)
Використовуючи рівняння Больцмана і формулу (2.20) матимемо, що ця кількість прямопропорційно залежить від тиску
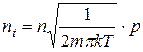 (3.2)
(3.2)
і маса молекул газу, що ударяються за одиницю часу у одиницю поверхні стінки ємності, в якій знаходиться газ буде дорівнювати
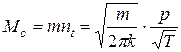 . (3.3)
. (3.3)
3. 2. Середня довжина вільного пробігу молекул
Незважаючи на хаотичність руху, відповідну частину свого шляху молекули газу проходять без зіткнень з іншими. Відстань, яку проходить молекула між двома послідовними зіткненнями, називають довжиною вільного пробігу молекули.
Середня довжина всіх прямолінійних відрізків шляхів, які молекула проходить між двома послідовними зіткненнями, називається середньою довжиною вільного пробігу молекули.
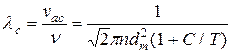 , (3.4)
, (3.4)
де 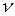 – число зіткнень молекули за за одиницю часу; d
– число зіткнень молекули за за одиницю часу; d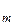 – діаметр молекули; С – постійна величина, яка називається постійною Сезерленда.
– діаметр молекули; С – постійна величина, яка називається постійною Сезерленда.
Знову використовуючи рівняння Больцмана одержимо, що середня довжина вільного пробігу молекули залежить від тиску і температури, тобто визначається концентрацією газу
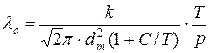 . (3.5)
. (3.5)
Для скорочення записів вводять величину d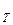 , яку називають ефективним діаметром молекули:
, яку називають ефективним діаметром молекули:
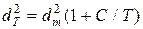 . (3.6)
. (3.6)
При p = 1 Па і T = 273 К для повітря середня довжина вільного пробігу молекули
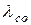 = 6.7
= 6.7  10
10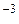 Па
Па  м. (3.7)
м. (3.7)
Тоді при будь-яких інших тисках для повітря
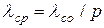 . (3.8)
. (3.8)
Під дією різних причин в газі можуть з’являтися вільні електрони, тобто додатково виникати електронний газ. Середня довжина вільного пробігу вільних електронів у газі
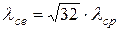 , (3.9)
, (3.9)
тобто не залежить від їх концентрації і діаметра.
3.3. Ефузія. Закон Грехема
Явище протікання газу під впливом різниці тисків через малий отвір у тонкій стінці називають ефузією газа.
Якщо в стінці є отвір (рис. 3.2), площа якого S, то маса газу (витрата газу), що проходить через цей отвір за одиницю часу, як це слідує з формули (3.3), буде дорівнювати
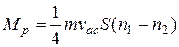 , (3.10)
, (3.10)
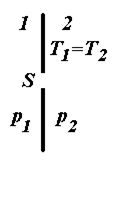 де
де 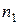 і
і 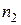 – концентрація молекул газу відповідно в області 1 і 2; (
– концентрація молекул газу відповідно в області 1 і 2; (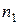 >
> 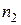 ), що знаходяться по обидва боки від отвору, при цьому вважаємо, що температура однакова.
), що знаходяться по обидва боки від отвору, при цьому вважаємо, що температура однакова.
Якщо виразимо 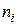 та
та 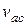 за формулами (2.4) і (2.17), одержимо закон Грехема
за формулами (2.4) і (2.17), одержимо закон Грехема
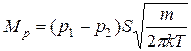 . (3.11)
. (3.11)
|
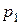 , тоді
, тоді
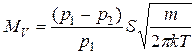 . (3.12)
. (3.12)
Слід зазначити(будемо вважати, що отвір круглий, діаметром D), що формули (3.11) і (3.12) справедливі, коли 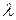
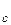 >> D, де
>> D, де 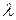
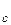 - середня довжина вільного пробігу молекул в області 1 або 2.
- середня довжина вільного пробігу молекул в області 1 або 2.
При 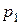 >>
>> (наприклад
(наприклад 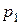 > 10
> 10 )
)
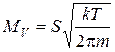 , (3.13)
, (3.13)
тобто об’єм газу, що пройде через отвір за тиском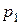 , не залежить від цього тиску. Якщо при атмосферному тискі
, не залежить від цього тиску. Якщо при атмосферному тискі 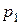 = 760 Торр у стінці вакуумної камери, де, наприклад, створено тиск
= 760 Торр у стінці вакуумної камери, де, наприклад, створено тиск  , з’явиться отвір діаметром 1 мм, то об’єм повітря (
, з’явиться отвір діаметром 1 мм, то об’єм повітря (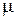 = 29) при 20
= 29) при 20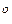 С, що буде надходити до камери за одну секунду, дорівнюватиме
С, що буде надходити до камери за одну секунду, дорівнюватиме
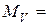 363 см
363 см 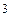 / c = 0, 363 л / с
/ c = 0, 363 л / с
3.4. Термічна ефузія
Якщо температура газу різна по обидва боки від отвору (Т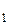 > Т
> Т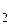 ), а початкові тиски однакові, то через деякий час виявиться, що тиски в області 1 і 2 будуть різними. При цьому
), а початкові тиски однакові, то через деякий час виявиться, що тиски в області 1 і 2 будуть різними. При цьому
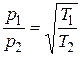 . (3.14)
. (3.14)
Явище зростання тиска в області, де газ має меншу температуру, в наслідок перетікання газу через отвір з області з більшою температурою називається термічною ефузією.
Запитання для самоперевірки
1. Що впливає на число молекул газу, що ударяються за одиницю часу в одиницю поверхні стінки ємності?
2. Дайте визначення середньої довжини вільного пробігу молекул у газі.
3. Що впливає на середню довжину вільного пробігу молекул?
4. Що називають ефузією в газі?
5. Сформулюйте закон Грехема.
6. Що виникає внаслідок термічної ефузії?
Лекція четверта
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1212; Нарушение авторских прав?; Мы поможем в написании вашей работы!