Число Кнудсена

Оскільки молекули газу окрім зіткнень між собою будуть мати ще зіткнення зі стінками трубопроводу, то очевидно, що течія газу залежатиме від співвідношення цих зіткнень.

Числом Кнудсена 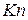називають відношення числа зіткнень молекул за одиницю часу зі стінками трубопроводу до числа зіткнень між собою:

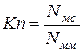. (5.1)

Число зіткнень молекул за одиницю часу зі стінками трубопроводу обернено залежить від характерного розміру, наприклад від діаметра d, якщо трубопровід є циліндричною трубою. Дійсно, чим більший радіус, тим менше це число. Число зіткнень молекул за одиницю часу між собою обернено залежить від середньої довжини вільного пробігу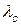. У зв’язку з цим, число Кнудсена визначається ще як

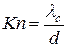. (5.2)

5. 2. Ступені вакууму

Газ у стані з тиском нижче атмосферного, тобто вакуум, може мати багато ступенів. У вакуумній техніці розрізняють такі три головні ступені вакууму, як низький, середній і високий, а також додатковий – надвисокий вакуум.

Явища, що протікають у газовому середовищі, дуже залежать від співвідношення зіткнень молекул як між собою, так і зі стінками посудини, що утримує газ, тому кількісно ступені вакууму можна характеризувати числом Кнудсена 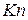, а також якісно ще за тиском або за середньою довжиною вільного пробігу молекул.

Вважається, що

низький вакуум 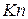<< 1; 760 > p >1 Торр; < 47 мк

середній - - - 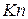~ 1; 1> p > 10 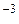Торр; 47 мк < 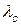< 50 мм

високий - - - 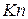> 1; 10 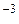> p > 10 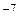Торр; 50 мм < 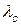< 0, 5 км

надвисокий - - - 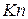>>1; p < 10 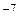Торр; 0, 5 км < 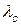~ 50 км

Слід пам’ятати, що ці ступені розрізняють умовно. Так, стан газу, який знаходиться у пористому твердому тілі, наприклад, у металі, відповідає високому вакууму навіть при атмосферному тиску газу, що знаходиться навколо тіла, тому що число Кнудсена у цьому випадку значно більше одиниці.

5.3. Режими течії газів. В’язкісний режим

У вакуумній техніці описання течії газу поділяють на три частини залежно від величини числа Кнудсена.

За великим тиском, коли середня довжина вільного пробігу молекул мала в порівнянні з діаметром трубопроводу (число Кнудсена мале), характер течії буде визначатися взаємодією між молекулами і газ можна розглядати як суцільне в’язке середовище, тому така течія називається в’язкісною, а режим течії газу - в’язкісним.

При низьких тисках середня довжина вільного пробігу молекул велика в порівнянні з діаметром трубопроводу (число Кнудсена велике) і течія газу визначається вєаємодією молекул зі стінками, тобто впливом стінок на вільний рух молекул. Вони рідко зтикаються між собою і кожна молекула рухається незалежно від інших. Такий режим течії газу називається молекулярним.

Перехідний проміжок між в’язкісним і молекулярним режимом характеризується проміжними значеннями числа Кнудсена, при цьому обидва типа зіткнень впливають на характер течії, тому і режим називають молекулярно- в’язкісним.

В’язкісний режим ще називають режимом Пуазейля. Число Кнудсена відповідає нерівності

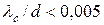. (5.3)

Якщо використовується повітря при 25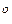С, то 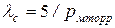(тиск у міліторрах), тоді в’язкісний режим (діаметр вимірюється в сантиметрах) буде визначатися нерівністю

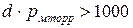[ мТорр 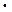см]. (5.4)

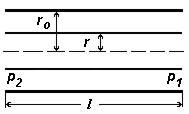Рис. 5.1.

Знайдемо, як буде визначатися витрата газу, тобто кількість газу, що перетікає за одиницю часу через трубопровід під дією позитивної різниці тисків 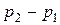. Для цього в трубопроводі, що має довжину l і радіус r 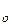, виділимо при осі симетрії малий елемент газового циліндра радіусом r рис. 5.1. При стаціонарній течії сили, що діють на цей елемент, будуть знаходитися в рівновазі. Ці сили можна розділити на два види:

сили, що виникають від дії різниці тисків і дорівнюють добутку цієї різниці на площу поперечного перерізу елемента

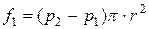; (5.5)

сили, що викликають гальмування і виникають під дією внутрішнього тертя, тобто

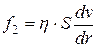, (5.6)

де S - бокова поверхня газового елемента, v - швидкість переміщення газу, а dr відповідає dx в (4.10).

Рівновага встановиться при 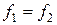. Отже

,

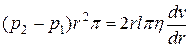тобто

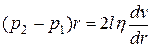
Після інтегрування отримаємо

.

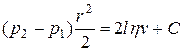Сталу інтегрування визначимо з умови, що при 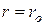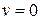. Тоді

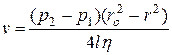. (5.7)

Можна побачити, що швидкість змінюється залежно від радіуса за параболічним законом (рис. 4.2). Тепер можна визначити об’ємну витрату газу - об’єм переміщеного газу за одиницю часу, який ще називають потоком газу, що вимірюється при середньому тиску в трубці 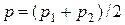, як

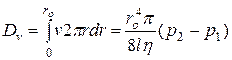, (5.8)

а масову витрату (в одиницях маси)

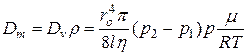. (5.9)

Дата добавления: 2014-01-07