Рівняння Бернуллі для ідеальної рідини

Рівняння Даніїла Бернуллі, отримане в 1738 р., є фундаментальним рівнянням гідродинаміки. Воно дає зв'язок між тиском P, середньою швидкістю υ і п'єзометричною висотою z у різних перерізах потоку й виражає закон збереження енергії рідини, що рухається. За допомогою цього рівняння вирішується велике коло завдань.

Розглянемо трубопровід змінного діаметра, розташований у просторі під кутом β (мал.3.5).

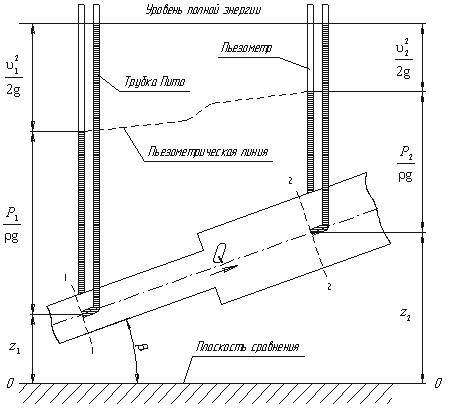
Мал.3.5. Схема до висновку рівняння Бернуллі для ідеальної рідини

Оберемо довільно на розглянутій ділянці трубопроводу два перерізи: переріз 1-1 і переріз 2-2. Нагору по трубопроводу від першого перерізу до другого рухається рідина, витрата якої дорівнює Q.

Для виміру тиску рідини застосовують п'єзометри - тонкостінні скляні трубки, у яких рідина піднімається на висоту 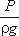. У кожному перерізі встановлені п'єзометри, у яких рівень рідини піднімається на різні висоти.

Крім п'єзометрів у кожному перерізі 1-1 і 2-2 установлена трубка, загнутий кінець якої спрямований назустріч потоку рідини, яка називається трубка Піто. Рідина в трубках П іто також піднімається на різні рівні, якщо відраховувати їх від п'єзометричної лінії.

П'єзометричну лінію можна побудувати в такий спосіб. Якщо між перерізом 1-1 і 2-2 поставити декілька таких самих п'єзометрів і через показання рівнів рідини в них провести криву, то ми отримаємо ламану лінію (мал.3.5).

Однак висота рівнів у трубках Піто щодо довільної горизонтальної прямої 0-0, що називається площиною порівняння, буде однакова.

Якщо через показання рівнів рідини в трубках Піто провести лінію, то вона буде горизонтальна, і буде відбивати рівень повної енергії трубопроводу.

Для двох довільних перерізів 1-1 і 2-2 потоку ідеальної рідини рівняння Бернуллі має такий вигляд:

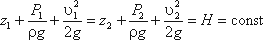
Так як перерізи 1-1 і 2-2 узяті довільно, то отримане рівняння можна переписати інакше:

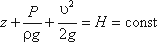
і прочитати так: сума трьох членів рівняння Бернуллі для будь-якого перерізу потоку ідеальної рідини є величина постійна.

З енергетичної точки зору кожний член рівняння являє собою певні види енергії:

z1 і z2 - питомі енергії положення, що характеризують потенційну енергію в перерізах 1-1 і 2-2;

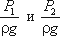- питомі енергії тиску, що характеризують потенційну енергію тиску в тих же перерізах;

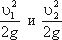- питомі кінетичні енергії в тих же перерізах.

Отже, згідно з рівнянням Бернуллі, повна питома енергія ідеальної рідини в будь-якому перерізі постійна.

Рівняння Бернуллі можна тлумачити й чисто геометрично. Справа в тому, що кожний член рівняння має лінійну розмірність. Дивлячись на мал.3.5, можна помітити, що z1 і z2 - геометричні висоти перерізів 1-1 і 2-2 над площиною порівняння;

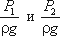- п'єзометричні висоти;

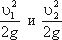- швидкісні висоти в зазначених перерізах.

У цьому випадку рівняння Бернуллі можна прочитати так: сума геометричної, п'єзометричної й швидкісної висоти для ідеальної рідини є величина постійна.

Дата добавления: 2014-01-07