Матриці

Для виконання перетворень векторів у просторі ми будемо використовувати матричний метод. Матрицею розмірності 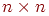називається таблиця чисел виду

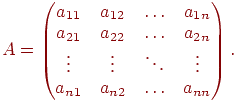
Надалі будемо використовувати скорочений запис для матриці: 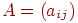. Рядка матриці 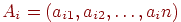будемо називати вектор- рядками (оскільки кожна з них визначає вектор), а стовпці 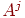- векторами-стовпцями. Матриці є ефективним інструментом для виконання перетворень на площині й у просторі. У цих випадках застосовуються матриці розмірності 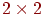й .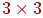

Спочатку введемо ряд операцій над матрицями й векторами.

Нехай задані матриці 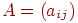й 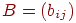. Сумою матриць називається матриця 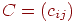, елементами якої є .

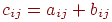Визначимо також операцію множення матриці на число. Результатом множення матриці 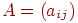на число 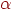є матриця 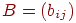, елементи якої .

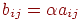Добутком двох матриць 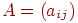і 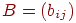називається матриця 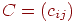, елементи якої визначаються в такий спосіб:

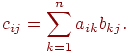
Добуток матриць некомутативно, тобто в загальному випадку .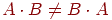

Попередні визначення ми вводили для матриць довільної розмірності. Наступні операції будуть пов'язані з векторами, і ми будемо мати на увазі, що або . Нехай задана матриця 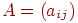й вектор 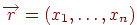. Результатом множення матриці на вектор є вектор 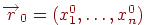, координати якого обчислюються як скалярний добуток рядка матриці на вектор:

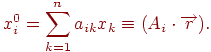
Якщо матриця 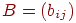отримана з матриці 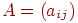шляхом заміни всіх вектор-рядків на вектори-стовпці, тобто 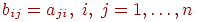, то неї називають транспонованою матрицею 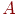й позначають .

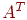Аналогічним образом визначається множення вектора на матрицю, тільки в цьому випадку вектор скалярно множиться на вектор-рядка матриці. Матриця виду

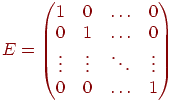
називається одиничної й має наступні властивості:

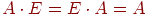- для будь-якої матриці .

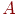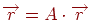- для будь-якого вектора .

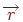- Якщо для матриці 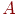існує матриця 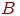, така, щ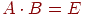о , то 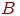називається зворотною матрицею до 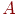і позначається . При цьому 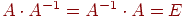, і для будь-якого вектора 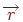одержуємо співвідношення: якщо , те .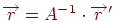

- Якщо для матриць 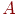і 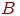існують зворотні матриці, то існує й зворотна матриця для їхнього добутку й .

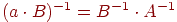Завдяки операції множення матриці на вектор будь-яка матриця визначає перетворення в просторі, по якому кожному вектору зіставляється деякий інший по цілком певному законі.

Відзначимо, що для геометричних перетворень зручно використовувати матриці розмірністю на одиницю більше, ніж розмірність простору, але про це докладніше мова йтиме в наступній главі.

Геометричні перетворення (перенос, масштабування, обертання)

Геометричні об'єкти на площині й у просторі можна піддавати ряду різних перетворень. Найбільш уживаними в завданнях комп'ютерної графіки є:

- переміщення (паралельний перенос);

- зміна розмірів (масштабування);

- повороти навколо деякої крапки на площині або деякій осі в просторі (обертання).

Надалі ми часто будемо ототожнювати крапки простору з радіус-вектором, обумовленим цією крапкою.

Спочатку розглянемо перетворення на площині, або двовимірні перетворення.

Паралельний перенос об'єкта зводиться до переміщення всіх його крапок на те саме відстань 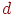у тому самому напрямку, заданому певним вектором 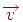. Якщо цей вектор має довжину 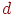, то операція переносу може бути реалізована шляхом додавання всіх крапок об'єкта з вектором 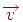. Досить просто довести, що при такій операції зберігаються відстані між крапками й, як наслідок, кути між відрізками. Зрозуміло також, що відрізки прямих перейдуть у відрізки прямих. Тому при переносі багатокутника немає необхідності піддавати цієї операції нескінченна безліч крапок, досить просто перенести вершини, а потім з'єднати їхніми відрізками.

Масштабування об'єкта можна реалізувати шляхом множення координат всіх його крапок на деяке число. Нехай є крапки з координатам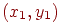и й 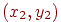, над якими виконується таке перетворення. Результатом будуть нові крапки з координатами й 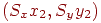. Якщо 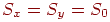, то нескладно довести, що обидві крапки перемістяться уздовж прямих, що проходять через саму крапку й початок координат, тобто в напрямку свій же радіус-вектора (рис. 4.5). При цьому відстань між новими крапками буде в 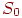раз відрізнятися від колишнього, але кути між відрізками збережуться (це можна показати, якщо виразити косинус кута через скалярний добуток векторів). Ясно, що якщо коефіцієнт масштабування 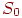більше одиниці, що відповідає відрізок розтягується, а якщо менше, те стискується. Крім того, при такому перетворенні об'єкт зміщається.

У випадку, коли 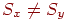, відстані між крапками зміняться нерівномірно, оскільки розтягання в горизонтальному й вертикальному напрямках будуть різними. Кути між відрізками також не збережуться (мал. 4.6).

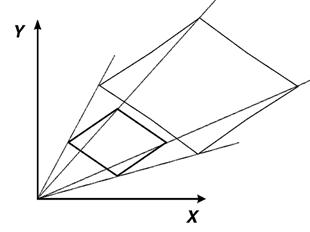
Рис. 4.5. Масштабування зі збереженням кутів

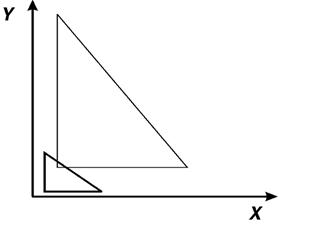
Рис. 4.6. Масштабування з перекручуванням кутів

Обертання в площині переміщають крапки по дузі окружності, центр якої перебуває на початку координат. Розглянемо спочатку рух однієї крапки при повороті на кут 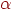(позитивним є напрямок проти годинникової стрілки), тобто поворот радіус-вектора на кут (мал. 4.7). Нехай крапка розташовувалася на відстані 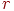від початку координат, а її радіус-вектор становив кут 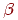з віссю абсцис. Тоді координати крапки визначаються формулами

Після повороту вектор буде становити кут , а нові координати крапки будуть визначатися співвідношеннями

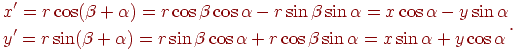
(4.7)

Можна показати, що при такому перетворенні зберігаються відстані між крапками, а отже, і кути між відрізками.

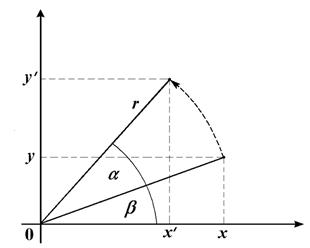
Рис. 4.7. Поворот на площині

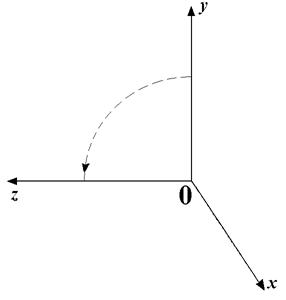
Рис. 4.8. Поворот у просторі

У випадку тривимірного простору міркування, що стосуються переносу й масштабування, повністю аналогічні, тільки вони поширюються на третю координату крапок. З обертанням же інша справа, оскільки тут обертовий рух є переміщення уздовж поверхні сфери й поворот на якийсь кут щодо крапки не можна визначити однозначно. Але переміщення з однієї крапки сфери в іншу завжди можна здійснити послідовністю поворотів щодо осей координат, тому виведемо формули для цих трьох обертань.

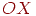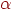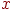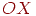При повороті щодо осі на кут у всіх крапок координата залишається незмінної. Якщо дивитися на площину з боку кінця осі , то осі будуть розташовані так, як показано на мал. 4.8. Позитивним уважається поворот від осі 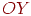до осі 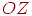. Якщо скористатися формулами для плоских поворотів, то координат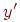и й 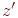нової крапки визначаються вираженнями

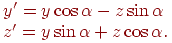
Формули повороту щодо осі 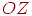повністю збігаються з тими, які минулого виведені для плоского випадку, а поворот щодо осі 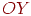виглядає так:

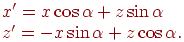
У всіх цих формулах варто звернути увагу на знаки, тому що вони залежать від того, який поворот уважається позитивним (у цьому випадку ми маємо справу із правою трійкою базисних векторів).

Перетворення масштабування й повороту на площині й у просторі можна виразити за допомогою матриць. Якщо задані коефіцієнти масштабування 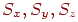, то перетворення крапки здійснюється за допомогою множення матриці на її радіус-вектор,

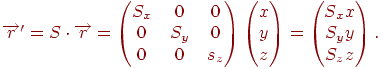
(4.8)

Двовимірний випадок виглядає подібним же чином.

Поворот на площині можна здійснити за допомогою матриці

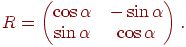
(4.9)

І нарешті, повороти в просторі щодо осей координат можна виконати за допомогою трьох матриць обертання

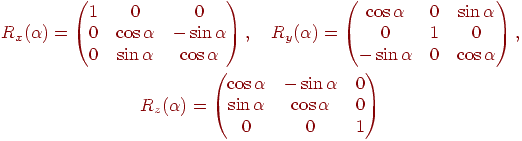
(4.10)

Неважко перевірити, що для матриць обертання справедливе співвідношення

Для виконання послідовних поворотів навколо осей на кути 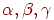можна створити матрицю перетворення шляхом перемножування трьох матриць:

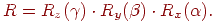
Використання цієї матриці дасть помітну економію в обчисленнях у порівнянні з послідовними множеннями на кожну із трьох матриць обертання.

Дата добавления: 2014-01-07