Кліпування багатокутників

Від завдання відсікання відрізків можна перейти до більше складного: кліпування довільних багатокутників. Якщо багатокутник неопуклий, то в результаті перетинання навіть із прямокутним вікном може вийти трохи не зв'язаних між собою фігур, як це показано на мал. 7.8.

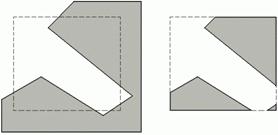
Рис. 7.8. Відсікання неопуклого багатокутника

Коли коштує завдання штрихування замкнутої області одночасно із завданням відсікання, те важливо правильно визначити приналежність знову отриманих фігур внутрішньої або зовнішньої частини вихідного багатокутника. Нехай вихідний багатокутник заданий упорядкованим списком вершин 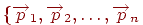, що відповідають ребрам . Для відсікання такого багатокутника прямокутним вікном можна застосувати алгоритм, запропонований Сазерлендом і Ходжменом. Ідея його полягає в послідовному відсіканні частини багатокутника прямими, що відповідають сторонам вікна. Результатом його роботи є впорядкований список вершин, що лежать у видимій частині вікна. На кожному кроці алгоритму утвориться деяка проміжна фігура, також представлена впорядкованим списком вершин і ребер. Приклад таких послідовних відсікань показаний на мал. 7.9. У процесі відсікання послідовно обходиться список вершин, причому кожна чергова крапка за винятком першої розглядається як кінцева крапка ребра, початковою крапкою якого є попередня крапка зі списку. Порядок, у якому розглядаються сторони вікна, не має значення. У процесі обходу формується список нових вершин багатокутника.

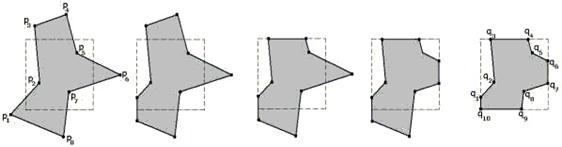
Рис. 7.9. Послідовні кроки клішування довільного багатокутника

На першому кроці для першої вершини в списку визначається її приналежність видимої області. Якщо вона видима, то вона стає першою крапкою першого оброблюваного ребра й заноситься в список нових вершин. Якщо ж вона невидима, то в список нових вершин не заноситься, але однаково стає першою крапкою ребра.

Для аналізованого ребра можливі чотири випадки розташування щодо вікна.

1. Ребро повністю видиме. Чергова крапка заноситься в список нових вершин (що предстоїть уже повинна перебувати в цьому списку, оскільки ребро повністю видиме).

2. Ребро повністю невидимо. Ніяких дій не виробляється.

3. Ребро виходить із області. Перебуває крапка перетинання ребра зі стороною вікна й заноситься в список нових ребер.

4. Ребро входить в область. Також відшукується крапка перетинання зі стороною вікна й заноситься в список нових вершин. Кінцева крапка теж заноситься в список нових вершин.

У цьому алгоритмі постійно доводиться визначати видимість крапки стосовно конкретного ребра вікна, що відтинає. Вікно також можна задати у вигляді впорядкованого списку вершин. Якщо обхід вершин вікна здійснюється за годинниковою стрілкою, то його внутрішня область буде розташована праворуч від границі. При цьому розташування крапки відносно прямій, який належить ребро, можна встановлювати різними способами:

1. Вибирається початкова крапка 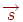даного ребра й будується вектор 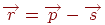і вектор внутрішньої нормалі до границі (ребру) вікна. Обчислюється скалярний добуток . Якщо , то крапка є видимою.

2. Будується просторовий вектор 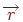(третю координату можна покласти рівної нулю). Вектор 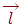(також просторовий, лежачий у тій же площині, що й ) спрямований уздовж ребра (з урахуванням напрямку обходу). Обчислюється векторний добуток 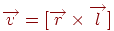. Якщо координата 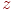у вектора 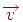позитивна, то крапка лежить праворуч від ребра (є видимою).

3. Виписується канонічне рівняння прямої, що проходить через ребро:

4.

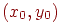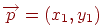5. Для довільної внутрішньої крапки вікна обчислюється значення , а також для крапки обчислюється . Якщо числа 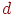й 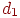мають однаковий знак, то крапка є видимою.

Найбільше просто ці алгоритми реалізуються у випадку відсікання прямокутним вікном зі сторонами, паралельними осям координат.

Дата добавления: 2014-01-07