Зафарбування методом Гуро

Плоске зафарбовування

Зафарбування граней

Якщо припустити, що джерело світла перебуває на нескінченності, то промені світла, що падають на поверхню, паралельні між собою. Якщо до цього додати умова, що спостерігач перебуває в нескінченно вилученій крапці, то ефектом ослаблення світла зі збільшенням відстані від джерела також можна зневажити. Крім того, таке положення спостерігача означає ще й те, що вектори, спрямовані від різних крапок поверхні до спостерігача, також будуть паралельні. При виконанні всіх цих умов, як треба з формули (11.6), плоска грань у всіх крапках має однакову інтенсивність висвітлення, тому вона зафарбовується одним кольором. Таке зафарбовування називається плоским.

Якщо ми апроксимуємо деяку гладку поверхню багатогранником, то при плоскому зафарбовуванні неминуче виявляться ребра, оскільки сусідні грані з різними напрямками нормалей мають різний колір. Ефект смуг Маху додатково підсилює цей недолік. Для його усунення при використанні цього способу зафарбовування можна лише збільшити число граней багатогранника, що приводить до збільшення обчислювальної складності алгоритму.

Один зі способів усунення дискретності интенсивностей зафарбовування був запропонований Гуро. Його метод полягає в тім, що використовуються не нормалі до плоских граней, а нормалі до аппроксимируемой поверхні, побудовані у вершинах багатогранника. Після цього обчислюються інтенсивності у вершинах, а потім у всіх внутрішніх крапках багатокутника виконується билинейная інтерполяція інтенсивності.

Метод сполучається з алгоритмом порядкового сканування. Після того як грань відображена на площину зображення, для кожної сканирующей рядки визначаються її крапки перетинання з ребрами. У цих крапках інтенсивність обчислюється за допомогою лінійної інтерполяції интенсивностей у вершинах ребра. Потім для всіх внутрішніх крапок багатокутника, що лежать на сканирующей рядку, також обчислюється інтенсивність методом лінійної інтерполяції двох отриманих значень. На мал. 11.5 показаний плоский багатокутник з обчисленими значеннями интенсивностей у вершинах.

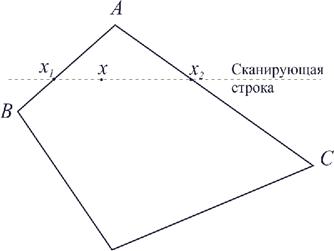
Рис. 11.5. Інтерполяція інтенсивності

Нехай 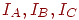- інтенсивності у вершинах 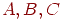, 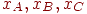- горизонтальні координати цих крапок. Тоді в крапках перетинання сканирующей рядка з ребрами багатокутника інтенсивності можна обчислити по формулах інтерполяції:

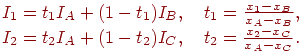
(11.7)

Після цього інтенсивність у крапці 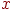одержуємо шляхом інтерполяції значень на кінцях відрізка:

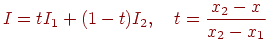
(11.8)

До недоліків методу Гуро варто віднести те, що він добре працює тільки з дифузійною моделлю відбиття. Форма відблисків на поверхні і їхнє розташування не можуть бути адекватно відтворені при інтерполяції на багатокутниках. Крім того, є проблема побудови нормалей до поверхні. В алгоритмі Гуро нормаль у вершині багатогранника обчислюється шляхом усереднення нормалей до граней, пов'язаним із цією вершиною. Така побудова сильно залежить від характеру розбивки.

Дата добавления: 2014-01-07