Більше складні моделі висвітлення

Коли ми розглядали алгоритми видалення невидимих ліній, передбачалося, що сцена включає тільки непрозорі об'єкти. У простої моделі висвітлення теж мова йшла про непрозорі поверхні. Тепер можна ускладнити завдання, включивши в модель не тільки відбиття світла, але й переломлення.

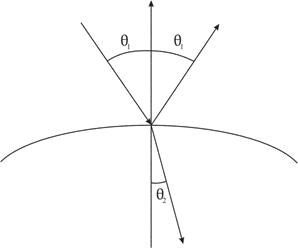
Рис. 11.7. Переломлений і відбитий промені

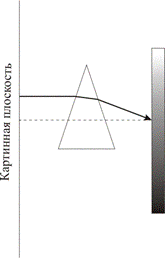
Рис. 11.8. Переломлення в призмі

При переході лучачи з одного середовища в іншу його напрямок змінюється відповідно до закону Синеллиуса: переломлений промінь лежить у площині, утвореною нормаллю до площини й падаючим променем, а кути, утворені променями з нормаллю, зв'язані формулою

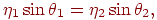
де 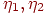- показники переломлення двох середовищ (мал. 11.7). Пропущення світла також може бути дифузійним (якщо частина енергії світла розсіюється середовищем) або спрямованим. У першому випадку ми маємо справу з напівпрозорими тілами, які змінюють фарбування видимих крізь них об'єктів. У другому випадку тіло є прозорим, і воно візуально виявляється тільки завдяки перекручуванням об'єктів за рахунок переломлення променів.

При наявності в просторовій сцені прозорих або напівпрозорих об'єктів треба враховувати, що зображення інших об'єктів буде відрізнятися від звичайної проекції на картинну площину (мал. 11.8). Ці ефекти добре знайомі всім, хто зіштовхувався з різними лінзами. Для побудови зображення таких сцен доцільно використовувати алгоритми зі зворотним трасуванням променів.

Для зображення напівпрозорих поверхонь без обліку переломлення можна ввести так званий коефіцієнт прозорості 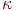, що дозволяє змішувати інтенсивності для видимої поверхні й тієї, що розташовано за нею:

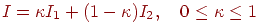
При поверхня непрозора, при - повністю прозора. Для напівпрозорих тіл необхідно враховувати їхню об'ємну структуру.

Методи побудови зображень сцен із прозорими й напівпрозорими об'єктами будуть більш докладно розглянуті в наступній лекції.

Усунення ступінчастості (антиэлайзинг)

При побудові растрового образа ліній (див. лекцию 8) ми зіштовхуємося з ефектом ступінчастості, пов'язаним з дискретизацією безперервного об'єкта. Перекручування ідеального образа відбувається тому, що із усього безлічі крапок ми вибираємо тільки ті, які виявляються ближче всього до центра елемента растра, і инициализируем цей елемент.

Рис. 11.9. Розподіл ваг при збільшенні дозволу в 4 рази

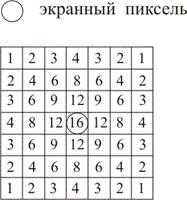
Рис. 11.10. Розподіл ваг при збільшенні дозволу в 16 разів

Для запобігання сильних перекручувань у цьому випадку можна, в- перших, підвищувати дозвіл растра, що дозволяє відображати усе більше дрібні деталі об'єктів. Але в цього підходу є свої чисто фізичні обмеження. Другий підхід полягає в тім, що растр розраховується з більше високим дозволом, а зображується з більше низьким - шляхом усереднення атрибутів пикселей першого більше детального растра з певними вагами. Якщо ваги однакові, то ми одержуємо рівномірне усереднення, як показано на мал. 11.9. Кращих результатів можна досягти, якщо використовувати різні ваги в пикселей першого растра. На мал. 11.10 показаний розподіл ваг при деталізації пикселя екранного растра.

Інший метод усунення ступінчастості полягає в тому, щоб розглядати пиксель не як крапку, а як деяку кінцеву область. В алгоритмах побудови растрового розгорнення пиксель уважається приналежної області зафарбовування, якщо його центр перебував усередині ідеального образа області. Якщо малюнок чорно^-білий, то усунути ефект ступінчастості растра практично неможливо. Але при наявності відтінків півтонів можна задати інтенсивність кольору пикселя залежно від площі його перетинання з областю.

Розглянемо застосування цього методу на прикладі розфарбування багатокутника. Ребро багатокутника будується з використанням алгоритму Брезенхема, описаного в лекции 8. Тут у цей алгоритм будуть внесені зміни, що включають параметр максимального числа рівнів интенсивностей. Визначаючи приналежність пикселя багатокутнику, ми будемо використовувати як помилка e частку площі, що належить ідеальній фігурі (мал. 11.11).

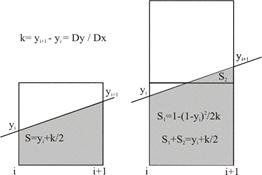
Рис. 11.11. площа, Що Відтинається відрізком, пикселя

Розглянемо знову випадок, коли відрізок спрямований у позитивний квадрант координатної площини під кутом, меншим . Ідеальний відрізок при заданому значенні целочисленной координати може перетинати один або два пикселя. У попередній версії алгоритму вибирався пиксель, центр якого розташовувався ближче до відрізка. Тепер інтенсивність для обох пикселей буде задаватися залежно від ступеня близькості кожного з них. Ініціалізація пикселя буде використовувати інтенсивність як параметр. Передбачається, що відрізок починається з кута першого пикселя, виходячи із чого й задається початкова інтенсивність. Блок-схема алгоритму наведена на мал. 11.12.

Усунення ефекту ступінчастості з математичної точки зору є завданням згладжування. Наведений тут алгоритм, що використовує площі перетинання растра й ідеального образа, можна описати за допомогою операції згортки функції. Спочатку дамо необхідні визначення. Сверткой функції 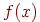називається інтеграл виду

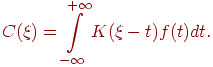
(11.9)

Функція 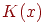називається ядром згортки. Як ядро згортки звичайно використовується або функція з кінцевим носієм (тобто відмінна від нуля лише на деякому кінцевому інтервалі), або швидко убутна на нескінченності функція (це може бути необхідною умовою існування інтеграла).

Розглянемо як свертываемой функція і ядра наступні функції:

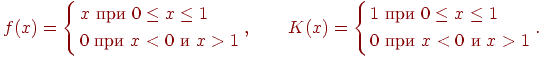
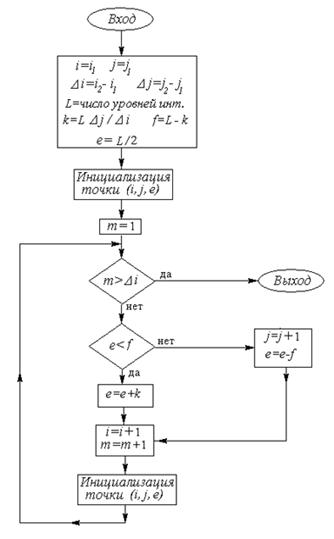
Рис. 11.12. Блок-схема модифікованого алгоритму Брезенхема

Тоді, у силу того, що подынтегральное вираження звертається в нуль 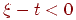при й при 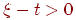, одержуємо

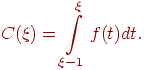
З огляду на вид функції 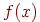, одержуємо, що згортка буде відмінна від нуля тільки на інтервалі 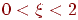. Значення згортки в деяких крапках наведені в таблиці 11.1.

Таблиця 11.1. Значення згортки у вузлах
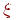
		1/2		3/2
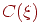
		1/8	1/2	3/8

Очевидно, що наша згортка дає площа перетинання трикутника, утвореного згортається функцией, що, із квадратом, підстава якого є відрізок 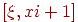на осі .

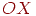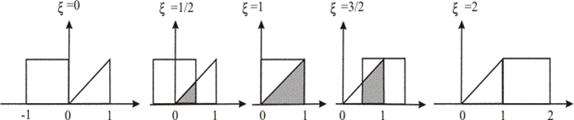
Рис. 11.13. Фігури, що відповідають значенням згортки з таблиці 11.1

На мал. 11.13 наведений вид перетинання для всіх п'яти випадків з таблиці 11.1. Якщо зрівняти ці результати з мал. 11.11, те видно, що значення згортки при 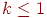дають площа тої частини пикселя, що перебуває усередині багатокутника (якщо вважати 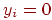), а при - суму площ двох пересічних пикселей.

На закінчення проілюструємо результат застосування алгоритму усунення ступінчастості на прикладі зображення, отриманого за допомогою програми Corel Draw. Ця програма являє собою розвитий графічний редактор, що дозволяє будувати об'єкти векторної графіки. На мал. 11.14 показане зображення простих графічних примітивів, попередньо переведене в растрову форму, на якому при великому збільшенні помітне згладжування із застосуванням відтінків сірого кольору.

Рис. 11.14. Згладжені зображення

Дата добавления: 2014-01-07