Статистичні показники

ТЕМА 4

План

4.1. Суть і види статистичних показників.

4.2. Абсолютні статистичні величини, одиниці їх вимірювання.

4.3. Характеристика відносних величин.

4.4. Середні величини, умови наукового їх застосування.

4.5. Середня арифметична, основні її властивості.

4.6. Середня гармонійна, її різновиди і сфера використання.

4.7. Характеристика середньої геометричної та середньої квадратичної величини.

4.8. Система статистичних показників.

4.1. Суть і види статистичних показників.

Інформація про суспільні явища і процеси створюється, передається і зберігається у вигляді статистичних показників. Вони є однією з основних економічних категорій, за допомогою яких відображають кількісну і якісну сторони стиму явищ і процесів.

З філософського погляду статистичний показник – це міра, тобто єдність якісного і кількісного відображення певної властивості соціально-економічного явища чи процесу.

Якісний зміст показника визначається суттю явища і відбивається в його назві. Кількісна сторона подається числом та його вимірником. Оскільки статистика вивчає суспільні явища в конкретних умовах простору і часу, значення будь-якого показника визначається щодо цих атрибутів.

Сполучною ланкою між якісним змістом і числовим вираженням є правило побудови – модель показника, яка розкриває його статистичну структуру. У моделі обгрунтовуються одиниці, узяті для вимірювання, технологія збирання даних, обчислювальні операції.

Модель показника має надзвичайно важливе значення для забезпечення вірогідності статистичної інформації. Як видно з рис. 4.1, від обгрунтованості моделі залежать обидва аспекти вірогідності такої інформації: адекватність відображення явища і точність вимірювання.

Адекватність розглядається як здатність показника відбити саме ту властивість, яка передбачена програмою дослідження

Точність і повнота вимірювання залежать від можливостей обліку, організації збирання та обробки даних. Отже.ю щоб показник відповідав своєму призначенню і виконував покладені на нього функції, на стадії його проектування потрібно з усіх боків логічно та статистично обгрунтувати модель.

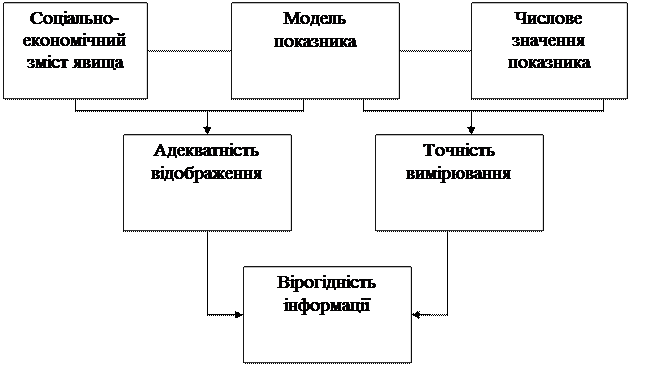
Рис. 4.1 Зв’язок статистичної моделі показника та вірогідності інформації

Статистичні показники розрізняють за способом обчислення, ознакою часою та аналітичними функціями.

За способом обчислення розглядають первинні і похідні показники. Первинні визначаються зведенням даних статистичного спостереження й подаються у формі абсолютних величин. Похідні показники обчислюються на базі первинних або похідних показників. Вони мають форму середніх або відносних величин.

За ознакою часу показники поділяються на інтервальні та моментні. Інтервальні характеризують явище за певний час (день, декаду, місяць.рік). До е стимуля відносять показники, що дають кількісну характеристику явищ на певний момент часу. Інтервальні та моментні показники можуть бути як первинними, так і похідними.

Інтервальні показники залежать від довжини періоду, за який вони обчислюються. Особливістю первинних інтервальних показників є адитивність, тобто можливість підсумовування. Похідні показники здебільшого неадитивні.

Серед статистичних показників існують пари взаємнообернених показників, які паралельно характеризують одне й те саме явище. Прямий показник X зростає з підсиленням явища, обернений 1/X, навпаки, зменшується. Прикладом можуть бути такі показники:

1) купівельна спроможність грошової одиниці – прямий показник, ціна одиниці товару – обернений;

2) продуктивність праці за одиницю часу – прямий показник, трудомісткість одиниці продукції – обернений.

Дата добавления: 2014-01-07