Характеристики центру розподілу: середня, мода, медіана

Ряд розподілу – основа аналізу закономірностей розподілу.

Ряди розподілу. Аналіз варіацій та форми розподілу

ТЕМА 5

План

5.1. Ряд розподілу – основа аналізу закономірностей розподілу.

5.2. Характеристики центру розподілу: середня, мода, медіана.

5.3. Сутність та показники варіації.

5.4. Характеристики форми розподілу.

Статистична сукупність формується під впливом причин та умов, з одного боку – типових, спільних для всіх елементів сукупності, а з іншого – випадкових, індивідуальних. Ці чинники взаємопов’язані, а їх спільні взаємодія визначає як індивідуальні значення ознак,так і розподіл останніх у межах сукупності. Характерні властивості структури статистичної сукупності відбиваються в рядах розподілу.

Ряд розподілу складається з двох елементів: варіант – значень групувальної ознаки Х та частот (часток) f. Саме у співвідношенні варіант і частот виявляється закономірність розподілу.

Залежно від статистичної природи варіант ряди розподілу поділяються на атрибутивні та варіаційні. Частотними характеристиками будь-якого ряду є абсолютна чисельність – частота, та відносна частота – частка. Додатковою характеристикою варіаційних рядів є кумулятивна частота (частка), що являє собою результат послідовного об’єднання груп і підсумовування відповідних їм частот (часток).

Поглиблений аналіз закономірностей розподілу передбачає характеристику зазначених особливостей сукупності, зокрема:

1) визначення типового рівня ознаки, який є центром тяжіння;

2) вимірювання варіації ознаки, ступеня згрупованості індивідуальних значень ознаки навколо центра розподілу;

3) оцінювання особливостей варіації, ступеня її відхилення від симетрії;

4) оцінювання нерівномірності розподілу значень між окремими елементами сукупності, тобто ступінь їх концентрації.

Базою аналізу закономірностей розподілу є варіаційний ряд – дискретний або інтервальний – з різними інтервалами.

Центром тяжіння будь-якої статистичної сукупності є типовий рівень ознаки, узагальнююча характеристика всього розмаїття її індивідуальних значень. Такою характеристикою є середня величина.

Окрім типового рівня важливе значення має домінанта, тобто найбільш поширене значення ознаки. Таке значення називають модою.

Модою називається величина ознаки (варіанта), яка найчастіше зустрічається в даній сукупності.

У дискретному ряду моду визначають безпосередньо за найбільшою частотою (часткою).

В інтервальному ряду за тим самим принципом визначається модальний інтервал, а потім конкретне модальне значення в середині інтервалу обчислюється за інтерполяційною формулою:

,

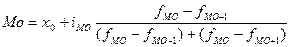де х₀ – нижня межа модального інтервалу;

і_МО – ширина модального інтервалу;

f_МО – частота модального інтервалу;

f_МО-1 – частота передмодального інтервалу;

f_МО+1 – частота післямодального інтервалу.

Для моди як домінанти число відхилень (х – Мо) мінімальне. Оскільки мода не належить від крайніх значень ознаки, то її доцільно використовувати тоді, коли ряд розподілу має невизначені межі.

Характеристикою центра розподілу вважається також медіана – значення ознаки, яка припадає на середину впорядкованого ряду, поділяє його навпіл – на два рівні за обсягом частини.

Щоб знайти медіану в дискретному варіаційному ряду, потрібно спочатку розташувати всі варіанти в зростаючому або спадаючому порядку. Потім визначити номер медіани, який вкаже на її розташування в рангованому ряді за формулою:

Щоб визначити медіану інтервального варіаційного ряду спочатку, за допомогою нагромаджених частот, потрібно знайти інтервал, що містить медіану. Значення медіани в середині інтервалу, як і значення моди, обчислюють за інтерполяційною формулою:

,

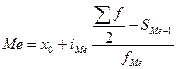де х₀ – нижня межа медіанного інтервалу;

і_Ме – ширина медіанного інтервалу;

f_Ме – частота модального інтервалу;

S_Ме-1 – кумулятивна частота передмедіанного інтервалу.

Медіана, як і мода, не залежить від крайніх значень ознаки; сума модулів відхилень варіант від медіани мінімальна, тобто вона має властивість лінійного мінімуму:

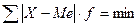
Цю властивість медіани можна використати при проектуванні розміщення зупинок міського транспорту, заготівельних пунктів тощо.

Окрім моди і медіани, в аналізі закономірностей розподілу використовуються також квартилі та децилі. Квартилі – це варіанти, які поділяють обсяги сукупності на чотири рівні частини, децилі – на десять рівних частин. Ці характеристики визначаються на основі кумулятивних частот (часток) за аналогією з медіаною, яка є другим кварти лем або п’ятим децилем.

Мода, медіана, квартилі і децилі відносяться до так званих порядкових

статистик, під якими розуміють варіант, який займає певне порядкове місце в

рангованому варіаційному ряду.

Їх використання в статистичному аналізі варіаційних рядів дозволяє більш глибоко дослідити і детальніше охарактеризувати сукупність, яка вивчається.

Дата добавления: 2014-01-07