Ітераційні методи розв’язування рівнянь. Принцип стискуючих відображень в метричному просторі

Нехай дано рівняння 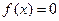(1). Суть полягає в наступному: нехай в деякій достатньо малій області Д існує єдиний розв’язок 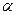рівняння (1). Вибираємо в цій області деяку точку 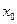(початкове наближення) достатньо близько до 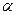і за допомогою співвідношення 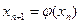(2) будуємо послідовність точок 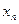: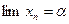(при 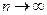). Вибираючи різними способами функцію 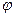будемо отримувати різні ітераційні методи.

Означення: метричним простором прийнято називати впорядковану пару 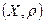, Х - множина елементів довільної природи, 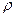- функція відстані, яка задовольняє наступним аксіомам:

1. 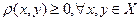, причому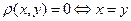

2.

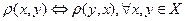
3.

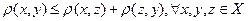
Теорема1: в повному метричному просторі Х задано оператор стиску А, тоді шснує єдина нерухома точка цього відображення, тобто рівняння 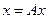має єдиний розв’язок, який може бути знайдений як границя послідовності .

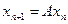Теорема2: нехай в повному метричному просторі Х або на його частині яка містить окіл S деякої точки 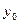, заданий параметр А. Нехай 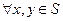виконуються умови:

1.

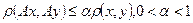
2.

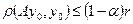
тоді в околі S існує єдиний розв’язок рівняння (3), який може бути отриманий як границя послідовності (4).

Означення: кажуть, що функція 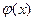на області Д задовольняє умову Лібшеця, якщо існує деяка стала К така, що .

Теорема3: нехай рівняння 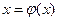має корінь 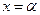в деякому крузі S: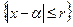і функція 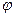в цьому крузі задовольняє умову Лібшеця з константою К<1, тоді яке б не було 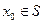послідовність 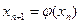(2)

буде збігатися до 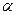причому швидкість збіжності характеризується нерівністю

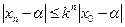(5).

Означення: умова Лібшеця з константою к<1, буде виконуватись якщо в околі точки 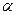має місце нерівність

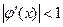, тоді умову (5) часто записують так

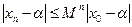, (6) .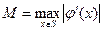

Дата добавления: 2014-01-07