Кусково-кубічна сплайн інтерполяція

Означення: Сплайном називається функція для якої існує поділ її області визначення на підобласті, такі що в середині кожної підобласті ця функція є многочленом деякого степеня 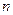. Крім того ця функція неперервна на області визначення разом зі своїми похідними до 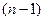порядку.

Найчастіше використовують випадок . Нехай на 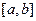задана неперервна функція 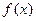, задане розбиття відрізка 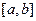точками: , 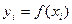для всіх .

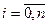Кубічним сплайном, який наближає дану функцію будемо називати функцію 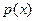, яка задовольняє наступні умови:

а) на кожному з відрізків ;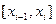

б) , , ;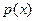

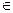
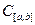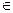
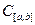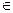
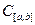в) для всіх .

Доведемо існування та єдність такого сплайну. Доведення носитиме конструктивний характер, тобто буде містити спосіб побудови сплайна. Будемо позначати через 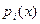ту частину сплайна, яка відповідає відрізку , .

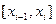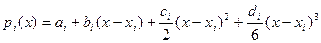,(1) де - коефіцієнти, які потрібно знайти.

,

.

З умови в) випливає 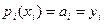.(2)

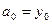
З того, що .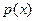

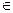
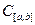
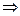
В (1) підставивши, отримаємо:

.

Позначимо .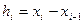

З останньої рівності будемо мати: .(3)

З того, що ,

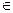
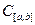
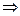
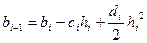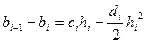, , (4) .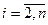

З того, що .

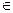
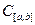
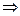
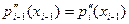Тобто , , 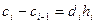(5) .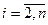

Об’єднуючи (3), (4) і (5) отримаємо систему рівняння з невідомими. Ще два рівняння дістанемо, якщо задамо деякі крайові умови для сплайна 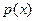. Наприклад: , тобт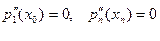о або , .

З рівнянь (3), (4), (5) виключимо коефіцієнти . Отримаємо деяку систему рівнянь, яка містить коефіцієнти .

З (3) , (*)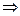

.

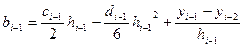Віднімемо дані рівності, і підставимо в (4), отримаємо: .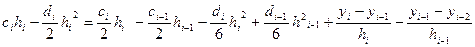

Звівши подібні доданки, отримаємо:

.(6)

З рівності (5) маємо: , . Підставимо дані рівності в (6), отримаємо: . Позбудемось індексу (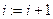): , (7), , .

Дана система має єдиний розв’язок. Розв’язавши одним з відомих методів систему (7) коефіцієнти шукаємо з (5) і (*).

Зауваження: ми вибирали граничні умови 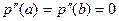, але в загальному випадку їх слід вибирати з властивостей функції, яку наближаємо.

Наприклад: нехай відомі 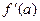, , то покладаємо , .

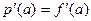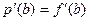Якщо в вузлах інтерполяції 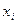функція, яку наближаємо задана не точно, а наближено, то немає смислу будувати сплайн, який в точках 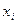набував би значення . Будують сплайн, який в точках 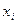проходить поблизу заданих значень . Такий процес називають сплайн-інтерполяцією з вирівнюванням.

Дата добавления: 2014-01-07