
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Многочлени Чебишева
|
|
|
|
 - позначаються,
- позначаються, 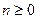 . Задаються наступними рівностями:
. Задаються наступними рівностями: 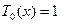 ,
, 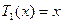 ,
, 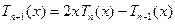 . (1) Використовуючи рекурентні формули (1), отримаємо:
. (1) Використовуючи рекурентні формули (1), отримаємо: 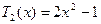 ,
, 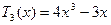 .
.
Відмітимо, що коефіцієнт біля 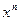 в многочлена
в многочлена  дорівнює
дорівнює 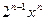 , всі многочлени з індексами
, всі многочлени з індексами 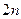 - парні, з індексами
- парні, з індексами 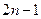 - непарні.
- непарні.
Відомо, що 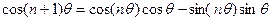 ,
,
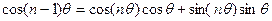
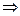
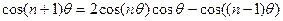
Позначимо 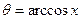 .
.
Отримаємо: 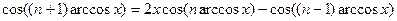 .(2)
.(2)
Порівнюючи (1) і (2) бачимо, що функція 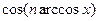 задовольняє рекурентне співвідношення (1). Початкові умови:
задовольняє рекурентне співвідношення (1). Початкові умови: 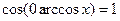 ,
, 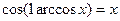 . Таким чином:
. Таким чином:
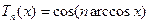 (3). З даної рівності випливає, що
(3). З даної рівності випливає, що 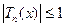 при
при 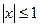 . (4)
. (4)
Зауваження: нерівність (4) не буде справедливою при всіх  . Якщо
. Якщо 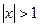 , то
, то 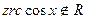 , а
, а 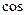 такого числа не завжди менше 1.
такого числа не завжди менше 1.
Рекурентне співвідношення (1) є різницевим рівнянням. Позначимо 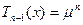 , тоді отримаємо характеристичне рівняння:
, тоді отримаємо характеристичне рівняння: 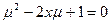
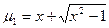
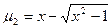
Якщо 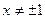 , то корені прості, а тому
, то корені прості, а тому 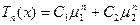 . Замість
. Замість 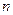 підставимо 1, отримаємо:
підставимо 1, отримаємо: 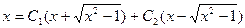 або
або 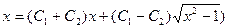
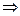
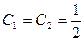 .
.
Тому 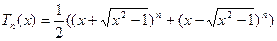 . (5)
. (5)
Зауваження: з нерівностей (4) випливає, що многочлени Чебишева набувають 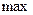 значення тоді, коли
значення тоді, коли 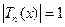 ,
, 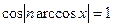 ,
, 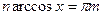 ,
, 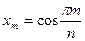 , де
, де 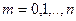 .
.
Многочлен 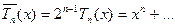 називають многочленом, який найменше відхиляється від нуля. Таке означення пояснюється наступною теоремою:
називають многочленом, який найменше відхиляється від нуля. Таке означення пояснюється наступною теоремою:
Теорема: Якщо 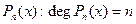 з старшим коефіцієнтом рівним одиниці, то
з старшим коефіцієнтом рівним одиниці, то 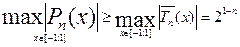 .
.
Теорема доводиться методом від супротивного.
Заміною змінної 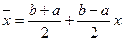 проміжок
проміжок 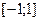 переводимо взаємно однозначно в проміжок
переводимо взаємно однозначно в проміжок 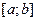 . Тоді многочлен
. Тоді многочлен 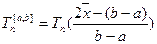 з старшим коефіцієнтом
з старшим коефіцієнтом 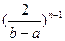 називається многочленом Чебишева на
називається многочленом Чебишева на 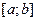 . Аналогічно як ми робили для
. Аналогічно як ми робили для 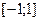 , можна побудувати многочлен, який найменше відхиляється на
, можна побудувати многочлен, який найменше відхиляється на 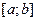 .
.
§18 НАБЛИЖЕННЯ ФУНКЦІЙ В ЛІНІЙНОМУ НОРМОВАНОМУ ПРОСТОРІ. УМОВИ ІСНУВАННЯ ТА ЄДНОСТІ ЕЛЕМЕНТА НАЙКРАЩОГО НАБЛИЖЕННЯ.
Нехай 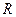 - лінійний нормований простір,
- лінійний нормований простір, 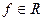 ,
, 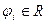 -лінійно-незалежні елементи. Через
-лінійно-незалежні елементи. Через 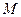 позначимо лінійний підпростір узагальнених многочленів виду
позначимо лінійний підпростір узагальнених многочленів виду 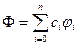 , де
, де 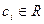 . Множина
. Множина 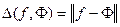 , де
, де 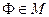 , обмежена знизу наприклад нулем. Тому існує
, обмежена знизу наприклад нулем. Тому існує 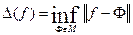 - найкраще наближення. Виникає питання чи в множині
- найкраще наближення. Виникає питання чи в множині 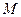 існує елемент
існує елемент 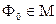 :
: 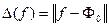 . Якщо такий елемент існує, то його називають елементом найкращого наближення функції
. Якщо такий елемент існує, то його називають елементом найкращого наближення функції 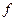 многочленами з множини
многочленами з множини 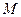 .
.
Теорема 1: Для 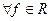 в множині
в множині 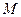 існує елемент найкращого наближення, множина таких елементів опукла.
існує елемент найкращого наближення, множина таких елементів опукла.
Зауваження: елемент найкращого наближення не обов’язково один. Наприклад, розглянемо простір 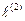 векторів
векторів 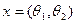 з нормою
з нормою 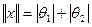 . Візьмемо точку
. Візьмемо точку 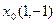 і візьмемо одновимірний підпростір
і візьмемо одновимірний підпростір 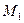 з базисними векторами
з базисними векторами 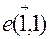 . Очевидно, що
. Очевидно, що 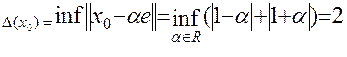 при
при 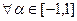 . Таким чином маєм нескінченну множину елементів найкращого наближення.
. Таким чином маєм нескінченну множину елементів найкращого наближення.
Теорема 2: Якщо простір 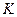 строго – нормований, то елемент найкращого наближення єдиний.
строго – нормований, то елемент найкращого наближення єдиний.
Теорема 3: (характеристика елемента найкращого наближення) Якщо в множині 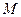 існує елемент
існує елемент 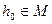 - елемент найкращого наближення для функції
- елемент найкращого наближення для функції 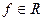 , то тоді для
, то тоді для 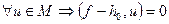 .
.
Теорема 4: Якщо  :
: 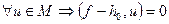 , то
, то 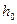 - елемент найкращого наближення.
- елемент найкращого наближення.
Як побудувати елемент найкращого наближення в просторі з скалярним добутком?
Нехай 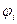 ,
, 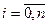 - лінійно-незалежні елементи. Комбінації
- лінійно-незалежні елементи. Комбінації 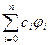 утворюють лінійний простір. Якщо деякий елемент
утворюють лінійний простір. Якщо деякий елемент 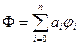 є елементом найкращого наближення для функції
є елементом найкращого наближення для функції 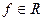 , то згідно з теоремою 3 різниця
, то згідно з теоремою 3 різниця 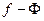 ортогональна до всіх елементів підпростору
ортогональна до всіх елементів підпростору 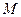 , в тому числі й до елементів
, в тому числі й до елементів 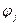 ,
, 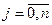 . Тобто
. Тобто 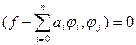 (1) для
(1) для 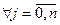 . Оскільки елемент найкращого наближення існує, то система (1) має розв’язок. Користуючись теоремою 4 можна довести, що
. Оскільки елемент найкращого наближення існує, то система (1) має розв’язок. Користуючись теоремою 4 можна довести, що 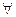 розв’язок системи (1) є елементом найкращого наближення функції
розв’язок системи (1) є елементом найкращого наближення функції 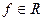 . Методом від супротивного можна довести, що такий елемент єдиний. Таким чином в просторі з скалярним добутком відшукання елемента найкращого наближення виду
. Методом від супротивного можна довести, що такий елемент єдиний. Таким чином в просторі з скалярним добутком відшукання елемента найкращого наближення виду 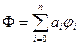 зводиться до розв’язання системи лінійних алгебраїчних рівнянь (1), яку зручніше записати у вигляді:
зводиться до розв’язання системи лінійних алгебраїчних рівнянь (1), яку зручніше записати у вигляді: 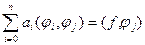 ,
, 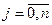 . (2)
. (2)
§19 СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ ФУНКЦІЙ.
N.1 НАБЛИЖЕННЯ АЛГЕБРАЇЧНИМИ МНОГОЧЛЕНАМИ.
Візьмемо метричний простір  функцій сумовних з квадратом, тобто функцій для яких виконується умова
функцій сумовних з квадратом, тобто функцій для яких виконується умова 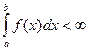 .
.
Для довільних функцій 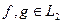 скалярний добуток задамо так:
скалярний добуток задамо так: 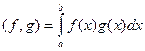 . Легко перевірити, що всі аксіоми скалярного добутку тут виконуються, якщо дві функції, які відрізняються на множині міри нуль вважати рівними.
. Легко перевірити, що всі аксіоми скалярного добутку тут виконуються, якщо дві функції, які відрізняються на множині міри нуль вважати рівними.
Означення: Найкраще наближення в просторі  називається найкращим середньоквадратичним наближенням або наближенням за методом найменших квадратів.
називається найкращим середньоквадратичним наближенням або наближенням за методом найменших квадратів.
В якості лінійно-незалежної системи візьмемо функції: 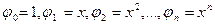 , елемент найкращого наближення будемо шукати в множині многочленів виду:
, елемент найкращого наближення будемо шукати в множині многочленів виду: 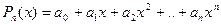 . Виходячи з загальної теорії стверджуємо, що многочлен найкращого наближення існує, для його побудови потрібно знайти розв’язок системи (2) з попереднього параграфа, вважаючи, що
. Виходячи з загальної теорії стверджуємо, що многочлен найкращого наближення існує, для його побудови потрібно знайти розв’язок системи (2) з попереднього параграфа, вважаючи, що 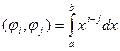 ,
,  .
.
Таким чином маємо систему з 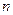 рівнянь:
рівнянь:
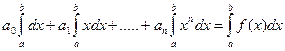 ;
;
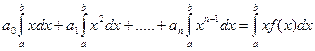 ; (1)
; (1)
.....................................................................
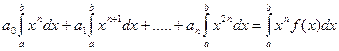 .
.
N. 2 ДИСКРЕТНЕ СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ.
Нехай функція 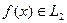 задана своїми значеннями в точках
задана своїми значеннями в точках 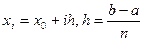 . Зауважимо, що ввівши змінну
. Зауважимо, що ввівши змінну  ми згадану систему точок переведемо в точки
ми згадану систему точок переведемо в точки 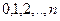 . Тому
. Тому 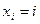 . Скалярний добуток означимо так:
. Скалярний добуток означимо так: 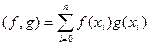 . В якості лінійно-незалежної системи функцій візьмемо многочлен Чебишева дискретного аргументу:
. В якості лінійно-незалежної системи функцій візьмемо многочлен Чебишева дискретного аргументу: 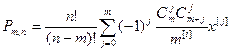 . Дані многочлени будуть ортогональними.
. Дані многочлени будуть ортогональними.
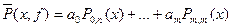 . Відповідно до загальної теорії для знаходження цього многочлена потрібно розв’язати систему:
. Відповідно до загальної теорії для знаходження цього многочлена потрібно розв’язати систему:  .
.
N.3 СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ ТРИГОНОМЕТРИЧНИМИ МНОГОЧЛЕНАМИ.
Розглянемо простір функцій сумовних з квадратом на відрізку  . Елемент найкращого наближення будемо шукати серед:
. Елемент найкращого наближення будемо шукати серед: 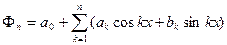 - тригонометричний многочлен степеня
- тригонометричний многочлен степеня 
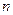 . В якості лінійно-незалежної системи функцій беремо ортонормовану систему
. В якості лінійно-незалежної системи функцій беремо ортонормовану систему 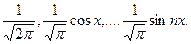 Розв’язавши систему (2) попереднього параграфа, отримаємо:
Розв’язавши систему (2) попереднього параграфа, отримаємо: 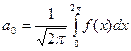 ,
, 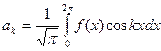 ,
, 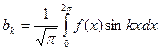 . Тобто найкраще середньоквадратичне наближення будуть давати частинні суми ряду Фур’є функції
. Тобто найкраще середньоквадратичне наближення будуть давати частинні суми ряду Фур’є функції 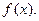
§21 НАЙКРАЩЕ РІВНОМІРНЕ НАБЛИЖЕННЯ. ТЕОРЕМА ЧЕБИШЕВА
Якщо норма в лінійному просторі визначена не через скалярний добуток, то пошук елемента найкращого наближення удосконалюється.
Нехай 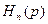 - множина многочленів степеня не вище
- множина многочленів степеня не вище 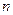 . Нехай також функція
. Нехай також функція 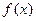 неперервна на
неперервна на 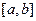 і візьмемо
і візьмемо 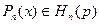 . Відхилення функції
. Відхилення функції 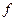 від множини
від множини 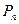 означається рівністю
означається рівністю 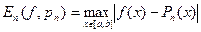 , нижню межу величини
, нижню межу величини  називають найменшим відхиленням.
називають найменшим відхиленням.
Критерій за яким визначають елемент найкращого наближення дає теорема.
Теорема Чебишева: нехай 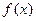 неперервна на
неперервна на 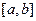 . Для того щоб
. Для того щоб 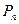 степеня не вище
степеня не вище 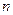 був многочлен найкращого наближення для функції
був многочлен найкращого наближення для функції 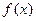 необхідно і достатньо щоб на відрізку
необхідно і достатньо щоб на відрізку 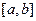 існувала хоча б одна система з
існувала хоча б одна система з 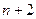 -х точок в якій різниця
-х точок в якій різниця 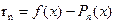 задовольняла б наступні умови:
задовольняла б наступні умови:
· Початково змінює знак
· Набуває найбільшого по модулю значення на 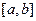 .
.
Означення: система про яку їде мова називається чебишевським альтернантом.
Означення: точка 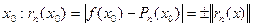 називатимемо е-точкою.
називатимемо е-точкою.
Означення: якщо в е-точці 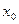 виконується
виконується 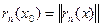 , то точку називають “+” точкою, а якщо
, то точку називають “+” точкою, а якщо 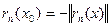 , то “-” точкою.
, то “-” точкою.
Доведення
1. покажемо, що на 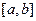 існують – і + точки. Оскільки
існують – і + точки. Оскільки 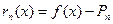 є функція неперервна на
є функція неперервна на 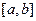 , то існують е-точки. Нехай наприклад не існує – точок, тоді існує
, то існують е-точки. Нехай наприклад не існує – точок, тоді існує 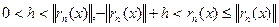 (1). Позначимо
(1). Позначимо 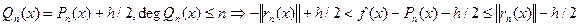 , тобто
, тобто 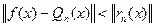 , тому многочлен
, тому многочлен 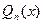 дає краще наближення ніж
дає краще наближення ніж 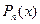 . Отримана суперечність “-”і “+” точки існують.
. Отримана суперечність “-”і “+” точки існують.
2. покажемо, що відрізок 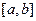 можна розбити на
можна розбити на 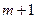 відрізок точками
відрізок точками 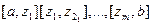 , так щоб кожен з отриманих відрізків містив лише “-“ або “+” точки. Нехай перша е-точка справа від а це “+” точка, тоді через
, так щоб кожен з отриманих відрізків містив лише “-“ або “+” точки. Нехай перша е-точка справа від а це “+” точка, тоді через 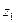 позначимо самий правий нуль величини
позначимо самий правий нуль величини 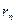 між точкою а та першою після неї “-” точкою.
між точкою а та першою після неї “-” точкою. 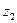 - самий правий нуль величини
- самий правий нуль величини 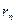 між точкою
між точкою 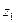 і першою після неї нуль точкою.
і першою після неї нуль точкою.
3. покажемо, що 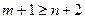 . Припустимо протилежне
. Припустимо протилежне 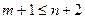 , тобто
, тобто 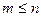 . На відрізку
. На відрізку 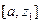 не має “-” точок на
не має “-” точок на 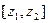 не має “+” точок..., тому існує число
не має “+” точок..., тому існує число  і таке, що
і таке, що 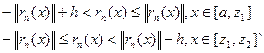 (2)
(2)
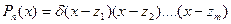
де 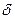 підберемо так щоб
підберемо так щоб
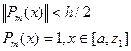
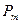 має той самий знак що й
має той самий знак що й 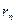
позначимо 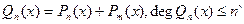 , якщо
, якщо 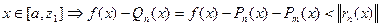 , якщо крім того враховується нерівність (2), то
, якщо крім того враховується нерівність (2), то  , аналогічно
, аналогічно 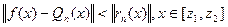 таким чином многочлен
таким чином многочлен 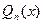 дає краще наближення ніж
дає краще наближення ніж 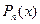 . Отримана суперечність доводить необхідність.
. Отримана суперечність доводить необхідність.
2. нехай многочлен 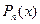 такий, що для нього виконуються умови 1 і 2 теореми. Доведемо, що він є многочленом найкращого наближення. Припустимо протилежне. Нехай
такий, що для нього виконуються умови 1 і 2 теореми. Доведемо, що він є многочленом найкращого наближення. Припустимо протилежне. Нехай 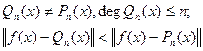 , тому в усіх точках
, тому в усіх точках 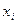 :
: 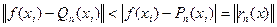 , тому в усіх точках
, тому в усіх точках 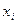 різниця
різниця 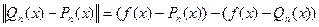 , має той самий знак, що і
, має той самий знак, що і 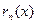 , тобто ця різниця змінює знак хоча б n+2 рази, тобто різниця
, тобто ця різниця змінює знак хоча б n+2 рази, тобто різниця 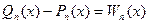 , степінь якої
, степінь якої  , має не менше n+1 коренів, що суперечить основній теоремі алгебри. Отримана суперечність доводить теорему.
, має не менше n+1 коренів, що суперечить основній теоремі алгебри. Отримана суперечність доводить теорему.
Теорема Чебишева: нехай на дійсній осі задано 2п періодична функція. Для того, щоб тригонометричний поліном  порядку не вище n був многочленом найкращого наближення для
порядку не вище n був многочленом найкращого наближення для 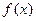 .необхідно і достатньо щоб на
.необхідно і достатньо щоб на 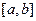 існувала хоча б одна з 2n+2 точок
існувала хоча б одна з 2n+2 точок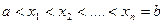 в яких різниця
в яких різниця 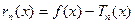 задовольняє умову:
задовольняє умову: 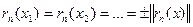 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2656; Нарушение авторских прав?; Мы поможем в написании вашей работы!