
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Побудова алгебраїчних многочленів найкращого наближення
|
|
|
|
Теорема Веєрштраса вказує що найкраще наближення існує, але не дає практичного способу побудови.
Ефективних способів точної побудови многочлена найкращого наближення до даної функції не існує. Тому розглянемо чисельні методи розв‘язку цієї задачі.
Зробимо деякі розрахунки які покажуть нам алгоритм побудови многочлена найкращого наближення.
І. Нехай на (а, b) задана неперервна f(x) і т 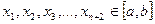 утворюють Чебишевський альтернант.
утворюють Чебишевський альтернант.
Зайдемо вираз для: 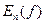 через значення функції в т згаданого альтернанту.
через значення функції в т згаданого альтернанту.
Нехай 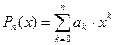 - многочлен найкращого наближення для
- многочлен найкращого наближення для 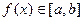 , тоді:
, тоді:
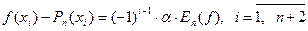 (1)
(1)
де: 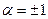
Розглянемо детермінант
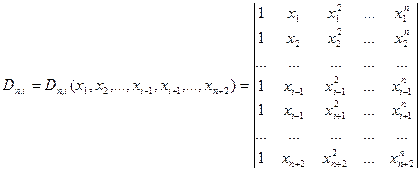
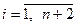 (2)
(2)
Усі детермінанти 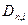 додатні бо
додатні бо 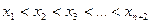 . Крім того
. Крім того
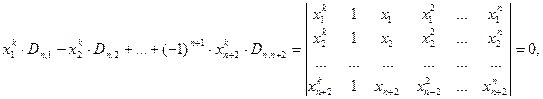
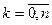 (3)
(3)
Рівність 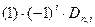 і просумуємо по
і просумуємо по 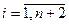
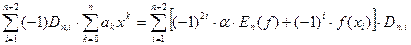 (4)
(4)
Розглянемо ліву частину (4), маємо що
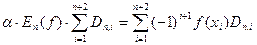 (5)
(5)
Введемо позначення:
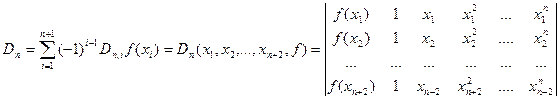
З (3) і останнього виразу (6) маємо:
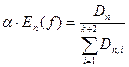 (7)
(7)
ІІ. Нехай 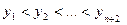 для довільної т. що
для довільної т. що 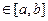
Покажемо, що:
1) 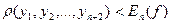 (8)
(8)
де: 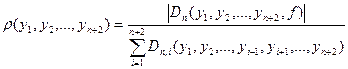
де: 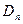 і
і 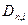 визначається за (6) і (2).
визначається за (6) і (2).
2) Існує т 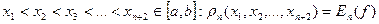 (9)
(9)
3) т 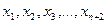 утворюють Чебишевський альтернанс а отже,:
утворюють Чебишевський альтернанс а отже,:
 (10)
(10)
де: 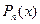 - многочлен найкращого наближення
- многочлен найкращого наближення 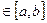
Позначимо 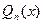 многочлен який найкраще наближає
многочлен який найкраще наближає 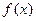 в точках
в точках 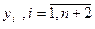
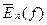 - найкраще наближення
- найкраще наближення 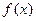 в т
в т 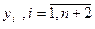
Нехай 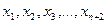 - Чебишевський альтернанс для
- Чебишевський альтернанс для 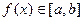 , тоді:
, тоді:
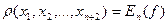
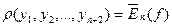
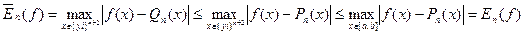
тобто:
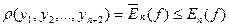
Якщо система точок 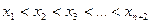 є Чебишевський альтернанс
є Чебишевський альтернанс 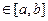 то:
то: 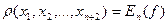 , а так як згідно теореми про існування найкращого наближення і Т. Чебишева цей альтернанс завжди існує, то
, а так як згідно теореми про існування найкращого наближення і Т. Чебишева цей альтернанс завжди існує, то 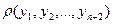 досягає верхньої межі на довільному з цих альтернантів.
досягає верхньої межі на довільному з цих альтернантів.
Нехай 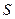 - множина точок
- множина точок 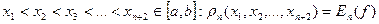
Нехай 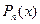 і
і 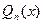 - многочлени найкращого наближення для
- многочлени найкращого наближення для 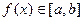 і на множині
і на множині 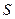 відповідно.
відповідно.
Аналогічно 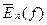 і
і 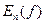 - найкраще наближення на
- найкраще наближення на 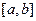 і
і 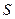 відповідно, тоді:
відповідно, тоді:
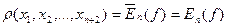
Оскільки 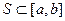 , то:
, то:
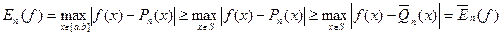
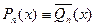
Множина точок 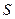 є альтернанс до
є альтернанс до 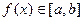 а отже, має місце (10)
а отже, має місце (10)
ІІІ. Алгоритм побудови многочлена найкращого наближення до 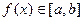
1) Беремо на 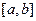 систему точок:
систему точок:
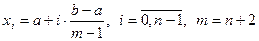
2) Нехай 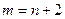 , тоді
, тоді
а) 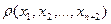 використовуючи (2), (6), (7), тоді
використовуючи (2), (6), (7), тоді 
Знаючи знак детермінанта 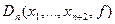 визначаємо знак різниці:
визначаємо знак різниці:
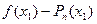 за (10)
за (10)
б) 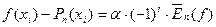
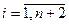 (11)
(11)
де: 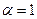 , якщо
, якщо 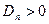
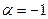 , якщо
, якщо 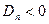
в) Розв‘язуємо систему і знаходимо:
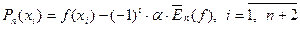 (12)
(12)
тобто знаходимо значення многочлена 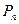 в т
в т 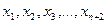 .
.
2) Знаходимо 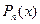 за інтерполяційними формулами в
за інтерполяційними формулами в 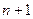 точці. Зайву точку можна використати для контролю бо інтерполяційний многочлен в цій точці повинен набувати наперед задане значення.
точці. Зайву точку можна використати для контролю бо інтерполяційний многочлен в цій точці повинен набувати наперед задане значення.
3) Якщо 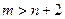 , то шукаємо всі можливі комбінації з
, то шукаємо всі можливі комбінації з 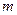 по
по 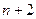 . Для кожної з них знаходимо:
. Для кожної з них знаходимо: 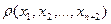 . Серед
. Серед 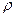 вибираємо найбільше знайдене значення і переходимо до пункту 2.
вибираємо найбільше знайдене значення і переходимо до пункту 2.
Зауваження: 1) Описаний алгоритм не є єдиний.
2) Можна довести що описаний процес рівномірно збігається до многочлена найкращого наближення.
3) Для збільшення точності потрібно збільшувати кількість точок поділу відрізка 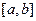 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 588; Нарушение авторских прав?; Мы поможем в написании вашей работы!