Метод сіток розв’язування крайових задач диференціальних рівнянь еліптичного типу

Нехай маємо:

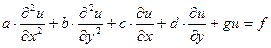(1)

де: a, b, c, d, g, f – деякі функції змінних х та у визначені в скінченій області G з межею Г.

Будемо вважати, що всі ці функції неперервні в області G+Г.

Функції a, b додатні в G+Г.

Завдання полягає в тому щоб знайти розв‘язок рівняння (1) неперервний аж до межі G який в точках межі Г набуває наперед заданих значень, тобто:

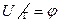
де: 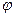- неперервна змінна х та у.

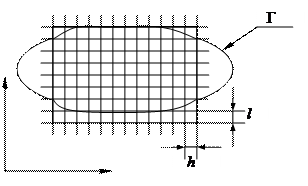
Будуємо сітку.

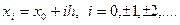
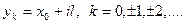
Означення: Два вузли називаються сусідніми, якщо вони віддалені один від одного на один крок.

Означення: Вузол називається внутрішнім, якщо всі сусідні 4 до нього вузли належать області G+Г.

Означення: Множина внутрішніх вузлів називається сітковою областю .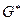

Означення: Ті вузли для яких хоч один з сусідніх який належить G+Г називається граничним. 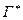- множина граничних вузлів.

Будемо позначати точку: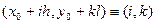

Щоб отримати з (1) різницеві рівняння похідні в кожній точці 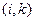замінимо на:

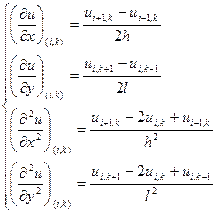(3)

Значення функцій a, b, c, d, g, f – в точці 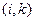будемо позначати:

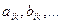
Підставивши значення похідних з (3) в (1) маємо:

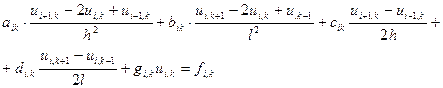(4)

Рівняння (4) можна записати для кожного внутрішнього вузла, якщо вузол 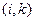є граничним, то:

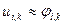(5)

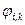- значення функції 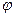в точці межі Г, яка найближча то точки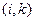

З (4) і (5) дають нам систему рівнянь яка рівна кількості невідомих. Розв’язавши її знайдемо наближені значення розв‘язку рівняння (1) в точках сітки.

Оцінимо похибку: Будемо вважати, що розв‘язок задачі має неперервні похідні до четвертого порядку включно. Розглянемо ряд Тейлора:

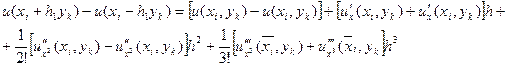
де: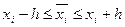

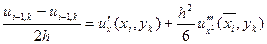
Будуючи розклад в ряд Тейлора виходять наступні формули:

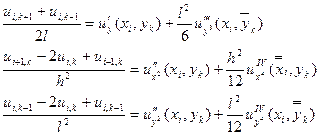
Підставивши отримані рівності в (4) маємо:

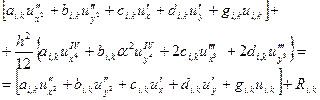(7)

де: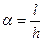

Якщо позначити через:

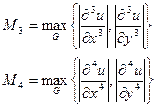
то виходячи з (7) похибку можна записати наступним чином:

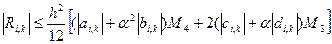(8)

Тобто, похибка має порядок 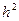оскільки:

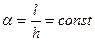
Зауваження: Якщо взяти рівняння Пуассона:

і квадратну сітку, то отримаємо рівняння:

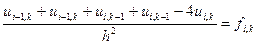(9)

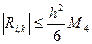
Зауваження: Інколи похідні у внутрішніх точках замінюють наступним співвідношеннями:

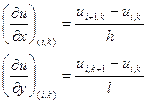
Тоді зміняться також різницеві рівняння.

Зауваження: Для побудови системи рівнянь (4) була використана наступна схема:

Це не є обов’язковим.

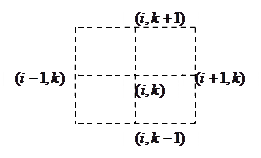
Система (4) зміниться:

Інший спосіб отримання різницевих рівнянь полягає в наступному:

Для того, щоб записати різницеве рівняння, яке наближає диференціальне рівняння (1) в вузлі 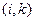розглянемо 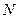вузлів які розміщені навколо точки 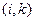певним способом для зручності позначимо вузол 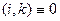, а всі інші від 0 до .

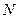Розглянемо лінійну комбінацію:

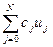
де коефіцієнти 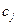- невизначені

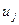- значення функції 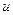в вузлі за номером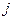

Вважаючи, що функція 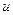має похідні достатньо високого порядку, розкладемо цю функцію в ряд Тейлора підставимо отриманий розв‘язок і згрупуємо члени з однаковим порядком похідних:

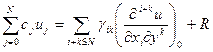(10)

де: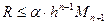

де: 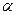- найменша відстань від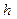

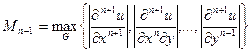
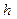- найменша відстань від вузла 0 до одного від всіх інших.

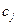- підбираємо так, щоб права частина (10) найменше відрізнялася від лівої частини рівняння (1) в вузлі 0.

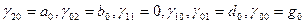, тобто:

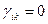, якщо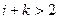

Якщо отримана система відносно 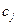матиме розв‘язок, то ми отримаємо деяке наближення розв‘язку рівняння.

Розглянемо приклади:

Рівняння Пуассона:

(11)

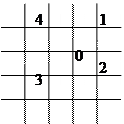
Будемо розглядати квадратну сітку з кроком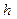

Для скорочення запису ліву частину рівняння (1) позначатимемо:

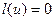(1‘)

У сітці вказані на малюнку вузли рівноправні і симетричні тому є смисл записати різницеву апроксимацію у вигляді:

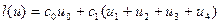
Вважаючи, що функція 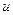має достатню кількість похідних, то розкладемо її в ряд Тейлора в околі вузла 0 і запишемо для кожного з вузлів:

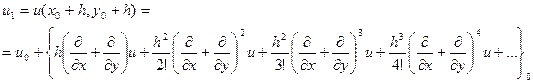
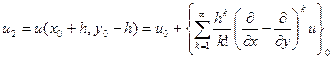
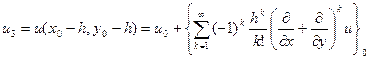
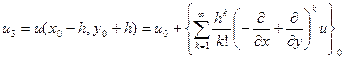
Тоді матимемо:

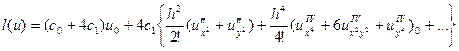
Щоб отримати наближення рівняння (11) треба, щоб:

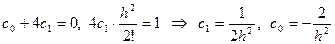
Маємо:

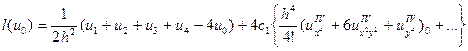
Відкинувши залишковий член отримаємо різницеве рівняння:

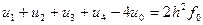(12)

Приклад2: Якщо для попереднього рівняння взяти іншу схему вузлів, тоді:

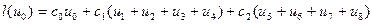
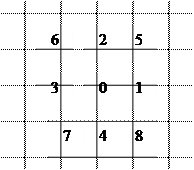Будуючи розклад як в попередньому прикладі і звівши подібні доданки маємо:

,

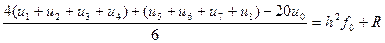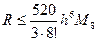
Будуючи різні схеми вузлів будемо отримувати різні апроксимації. Причому сітка не обов’язково трикутна.

Зауваження: 1) Щоб зменшити похибку при наближенні граничних умов часто виконують екстраполяцію розв‘язку на межу області по знайдених значеннях функцій у внутрішніх точках області.

2) На практиці для оцінки похибки часто використовують принцип Рунге:

Нехай відомо, що порядок похибки розв‘язку при використанні квадратної сітки з кроком 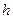рівний 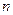, тобто:

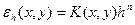
Будуємо розв‘язки 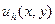і 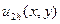з кроком 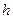та 2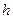відповідно, тоді:

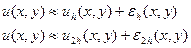
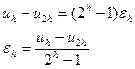
Дата добавления: 2014-01-07