Логічні елементи

Перетворення

Операції з|із| двійковими числами

У ЕОМ застосовують позиційні системи прочитування з|із| недесятковою підставою|заснуванням|: 2, 8, 16

Найбільше поширення набула двійкова система прочитування. Її найпростіше реалізовувати двійкових позиційних пристроїв|устроїв|. Вона дає можливість|спроможність| спростити виконання арифметичних дій.

Двійкова система вимагає 2 цифри 0 і 1, підставою|заснуванням| цієї системи – 2. Воно записується|занотовує| в наступній|слідуючій| формі:

10₂ = 1 · 21 + 0 · 20

Правила побудови|шикування| чисел в двійковій системі ті ж, що і в десятковій: як тільки|як тільки| рахунок дійшов до старшої цифри (у десятковій – 9, а в двійковій – 1) необхідно записати 0 і перенести 1 в старший розряд. Число > 9 в десятковій системі і > 1 в двійковій записати тільки|лише| двозначним| числом.

Перетворення двійкових чисел в десяткові:

Приклад 1. 10102 = 1 · 23 + 0 · 22 + 1 · 21 + 0 · 20 = 8 + 0 + 2 + 0 = 1010

Приклад 2. 101.0112 = 1 · 22 + 0 · 21 + 1 · 20 + 0 · 2-1 + 1 · 2-2 + 1 · 2-3 =

= 4 + 1 + 0 + 0,25 + 0,125 = 5,375₁₀.

Перетворення десяткових чисел в двійкові:

Спільне правило переказу. Для переказу цілого числа N, представлену в системі прочитування з підставою q в систему з підставою р необхідне дане число послідовно ділити на підставу системи р до тих пір, поки останнє приватне не буде < р.

Число N в системі р представиться у вигляді впорядкованої послідовності залишків ділення, причому старшу цифру числа N дає останнє приватне.

Приклад 3. Перетворити десяткове число 10₁₀ в двійкове:

крок	Ділення	Результат	Залишок (двійкове число)
	10: 2		0 (М.З.Р)
	5: 2
	2: 2
	1: 2		1 (С.З.Р)

Отримуємо: 10₁₀ = 1010₂

Приклад 4. Перетворити десятковий дріб 0,375₁₀ в двійкове число:

Множення	Двійкове число
2 · 0,375 = 0,75	0 (оскільки < 1, то С.З.Р. = 0)
2 · 0, 75 = 1,5	1 (оскільки > 1, то С.З.Р. = 1)
2 · 0,5 = 1
2 · 0 = 0	0 (М.З.Р)

Отримуємо: 0,375₁₀ = 0.0110₂

Перевірка: 0.0110₂ = 0 · 20 + 0 · 2^-1 + 1 · 2^-2 + 1 · 2^-3 = 0,25 + 0,125 = 0,375₁₀

Приклад 5. Перетворити десяткове число 12,125₁₀ в двійкове:

Ціле число	Десятковий дріб
Щаг	Ділення	Залишок|остача| (двійкове число)	Крок	Множення	Двійкове число
	12: 2 = 6	0 (М.З.Р)		0.125 · 2 = 0,25	0 (С.З.Р)
	6: 2 = 3			0.25 · 2 = 0,5
	3: 2 = 1			0.5 · 2 = 1
	1: 2 = 0	1 (С.З.Р)		0 · 2 = 0	0 (М.З.Р)

Отримуємо: 12,125₁₀ = 1100.001₂

Перевірка: 1100.001₂= 1 · 23 + 0 · 22 + 1 · 2-3 = 8 +4 + 0,125 = 12,125₁₀

2⁰ = 1 2^-1 = 0,5

2¹ = 2 2^-2 = 0,25

2² = 4 2^-3 = 0,125

2³ = 8 2^-4 = 0,0625

2⁴ = 16 2^-5 = 0,03125

2⁵ = 32 2^-6 = 0,015625

2⁶ = 64 2^-7 = 0,0078125

2⁷ = 128

2⁸ = 256

2⁹ = 512

2¹⁰= 1024

Складання двійкових чисел

Спільні правила: 0+0 = 0; 0+1 = 1; 1+1 = 10

Приклад 6. Скласти два числа 4510+1110=5610

45₁₀ = 101101₂ ; 11₁₀ = 001011₂; 56₁₀ = 111000₂

+	001011	(2^5 + 2^3 + 2^2 + 2^0 = 32 + 8 + 4 +1 = 4510 )
(2^3 + 2^1 + 2^0= 8 + 2 +1 = 1110 )
	(2^5 + 2^4+ 2^3 = 32 + 16 + 8 = 5410 )

Приклад 7. Скласти два числа 2,3₁₀+2,4₁₀=4,7₁₀

	Множення	Двоїч.число	Множення	Двоїч.число
210 = 102	0,3 · 2 = 0,6	0 (С.З.Р)	0,4 · 2 = 0,8	0 (С.З.Р)
	0,6 · 2 = 1,2		0,8 · 2 = 1,6
	0,2 · 2 = 0,4		0,6 · 2 = 1,2
	0,4 · 2 = 0,8		0,2 · 2 = 0,4
	0,8 · 2 = 1,6		0,4 · 2 = 0,8
	0,6 · 2 = 1,2	1(М.З.Р)	0,8 · 2 = 1,6	1(М.З.Р)
	10.010011 10.011001 100.101100
+

+	10.010 10.011 100.101

100.1011001₂ = 2² + 2^-1 + 2^-3 + 2^-4 = 4 + 0,5 + 0,125 + 0,0625 = 4,6875₁₀

100.101₂ = 2² + 2^-1 + 2^-3 = 4 + 0,5 + 0,125 = 4,625₁₀

Таблиця відповідності різних систем прочитування

Десятіч-на	Двоїч-на	Восьмі-річна	16-рич-на	Десяті-чна	Двоїч-на	Восьмі-річна	16-рич- на
			А				1А
			В				1В
			C				1С
			D				1D
			E				1E
			F				1F

Приклад 7. Перетворити десяткове число 634₁₀ у вісімкове:

крок	Ділення	приватне	Залишок (двійкове число)
	634: 8		2 (М.З.Р)
	79: 8
	9: 8
	1: 8		1 (С.З.Р)

634₁₀ = 1172₈

1172₈ = 1 · 83 + 1 · 82 + 7 · 81 + 2 · 80 = 512+ 64 + 56 + 2 = 634₁₀

Приклад 8. Перетворити вісімкове число 35₈ в двійкове:

35₈ = 3 · 81 + 5 · 80 = 24 + 5 = 29₁₀

крок	Ділення	приватне	Залишок (двійкове число)
	29: 2		1 (М.З.Р)
	14: 2
	7: 2
	3: 2
	1: 2		1 (С.З.Р)

35₈ = 29₁₀ = 11101₂

11101₂ = 1 · 24 + 1 · 23 +1 · 22 + 1 · 20 = 16 + 8 + 4 + 1 = 29₁₀

Логічними елементами називають прості цифрові пристрої, призначені для реалізації функцій алгебри логіки за допомогою електричних сигналів. Найбільш поширені потенційні логічні елементи, в яких існує зв'язок по постійному струму між входами і виходами.

Основною електричною характеристикою логічного елементу є передавальна характеристика – залежність вихідної напруги від напруги на одному з входів. Знімається характеристика в умовах, за яких змінюється напруга на одному з входів логічного елемента, а на решті входів вона підтримується постійною.

Логічні елементи, які досліджуються в цій лабораторній роботі належать до класу комбінаційних. Це означає, що їх вихідні сигнали визначаються тільки сукупністю сигналів, які діють на входах в даний момент часу, та не залежать від сигналів, які діяли на входах раніше.

Найважливішими функціональними параметрами логічних елементів є функція алгебри логіки, яка ними реалізується, а також коефіцієнт розгалуження К_роз по виходу і коефіцієнт об’єднання К _об по входу.

К_роз дорівнює числу входів інших елементів, які можна підключити до виходу даного елемента. К _об дорівнює числу входів, передбачених схемою логічного елемента. Майже в усіх елементах, які досліджуються в даній лабораторній роботі, К _об=2.

В залежності від схемотехнічних рішень використаних для побудови логічних елементів розрізняють

транзисторно-транзисторну логіку (ТТЛ), побудовану на біполярних транзисторах,

емітерно- зв′язану логіку (ЕСЛ),

інтегрально- інжекційну логіку (І²Л),

логіку на однотипних уніполярних транзисторах (п-МОП та р-МОП),

логіку на різнотипних уніполярних транзисторах, так звану комплементарну логіку (КМОП).

Існують інші схемотехнічні рішення логічних елементів, але їх практичне застосування обмежене.

Як відомо, функції алгебри логіки і їх аргументи можуть приймати ь лише два значення - 0 та 1. Тому вхідні і вихідні сигнали логічних елементів повинні приймати тільки два значення. Це досягається конструкцією вихідних каскадів логічних елементів і способами управління ними. Тут розрізняють елементи з позитивною та негативною логіками. В елементах з позитивною логікою значенню сигналу 1 відповідаєбільшезначення напруги, а значенню сигналу 0 менше значення напруги, в елементах з негативною логікою – навпаки. На рис.9.1. наведені схеми умовного позначення основних логічних елементів.

Рис.9.1.

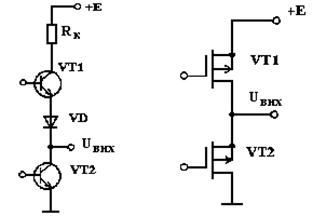
На рис. 9.2. представлені схеми вихідних каскадів елементу транзисторно - транзисторної логіки (ТТЛ) (рис. 9.2.а) і елементу на МОП - транзисторах.. (рис. 9.2.б).

Транзистори вихідних каскадів працюють в ключовому режимі. Якщо транзистор VT2 відкритий, а VT1 - закритий, то на виході - сигнал низької напруги, який відповідає нульовому стану виходу - "логічний нуль". Якщо VT2 - закритий, а VT1 - відкритий, то на виході висока напруга - "логічна одиниця". Існують логічні елементи, схеми яких можуть набувати стан, при якому закриті і VT1 і VT2. Такий стан носить назву «високий імпеданс виходу».

Схемотехнічним рішенням логічного елементу визначаються діапазони напруг, які закріплюються за одиничним та нульовим значеннями сигналів.

а) б)

Рис.9.2.

Існують також логічні елементи, вихідний каскад яких складається з транзистора з розімкненим колекторним колом, вони носять назву елементів з відкритим колектором. Ці елементи вимагають підключення зовнішнього навантаження (рис. 9.3).

Рис.9.3.

Логічний зв'язок будь-якої складності можна аналітично виразити,

використовуючи обмежений набір елементарних логічних функцій. Такий

набір називається функціонально повною системою логічних функцій.

У даній роботі досліджуються три функціонально повних системи. В одну з них входять три логічні функції: інверсія, диз'юнкція, кон'юнкція. Друга і третя функціонально повні системи містять тільки одну функцію: штрих Шеффера або стрілку Пірса.

У основі роботи логічних елементів лежать принципи, викладені в булевій алгебрі:

0´0=0 0+0=0

0´1=0 0+1=1

1´0=0 1+0=1

1´1=1 1+1=1

Аналітично функції, які реалізуються логічними елементами, виражаються так:

- диз'юнкція (логічне додавання) 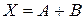, (АБО)

- кон'юнкція (логічне множення) , (І)

- інверсія (логічне заперечення) , (НІ)

- інверсія диз'юнкції (стрілка Пірса) , (АБО-НІ)

- інверсія кон'юнкції (штрих Шеффера) , (І-НІ)

- нерівнозначність; додавання по модулю 2 ,

(АБО, яке виключає).

Логіку, закладену в ці функції, можна сформулювати таким чином:

- якщо функція Х набуває значення 1 тоді, коли хоча б один аргумент дорівнює 1, це – логічне додавання;

- якщо функція Х набуває значення 1 тільки тоді, коли всі (в даному випадку обидва) аргументи дорівнюють 1, це – логічне множення;

- якщо функція Х дорівнює 1, коли її аргумент дорівнює 0 та навпаки, це – логічне заперечення;

- якщо функція Х набуває значення 0, коли хоча б один аргумент дорівнює 1, це – стрілка Пірса;

якщо функція Х набуває значення 0, тільки коли всі (в даному випадку

- обидва) аргументи дорівнюють 1, це – штрих Шеффера;

- якщо функція Х набуває значення 1, тільки коли обидва аргументи мають різні значення, це – нерівнозначність.

Дата добавления: 2014-01-07