Задачі для закріплення лекційного матеріалу

Контрольні запитання до матеріалу лекції

3.1. Охарактеризуйте поняття «сигнал».

3.2. Що є основним параметром сигналу?

3.3. Які характерні особливості притаманні електро- і радіосигналам?

3.4. Що таке «детермінований сигнал»?

3.5. Що таке «дискретний сигнал»?

3.6. Що таке «аналоговий сигнал»?

3.7. Що таке «постійний сигнал»?

3.8. Що таке «змінний сигнал»?

3.9. Якою є основна ознака періодичного сигналу?

3.10. Що таке «миттєве значення параметра сигналу»?

3.11. Що таке «пікові значення параметра сигналу»?

3.12. Що таке «розмах значень параметра сигналу»?

3.13. Що ми називаємо «гармонічним сигналом»?

3.14. Охарактеризуйте інтегральні параметри періодичних сигналів

3.15. Що таке «постійна складова» змінного сигналу?

3.16. Що таке «ефективна напруга»?

3.17. Що таке «діюча напруга»?

3.18. Що таке «коефіцієнт форми змінного сигналу»?

3.19. Що таке «коефіцієнт амплітуди змінного сигналу»?

3.20. Охарактеризуйте розподіл змінних сигналів за спектром їх частот.

3.21. Що таке «імпульсний сигнал»?

3.22. Що таке «відеоімпульс»?

3.23. Що таке «радіоімпульс»?

3.24. Що ми розуміємо під поняттям «прямокутний імпульс»?

3.25. Охарактеризуйте основні параметри прямокутних імпульсів.

3.26. Що таке «передній фронт» прямокутного імпульсу?

3.27. По якому рівню визначається тривалість переднього фронту прямокутного імпульсу?

3.28. Що таке «задній фронт» прямокутного імпульсу?

3.29. По якому рівню визначається тривалість заднього фронту прямокутного імпульсу?

3.30. Що таке «вершина» прямокутного імпульсу?

3.31. По якому рівню визначається тривалість вершини прямокутного імпульсу?

3.32. Що таке «тривалість» прямокутного імпульсу?

3.33. По якому рівню визначається тривалість прямокутного імпульсу?

3.34. Що таке «викиди» на епюрах (осцилограмах) прямокутних імпульсів?

3.35. Що таке «шпаруватість» для періодичної послідовності прямокутних імпульсів?

3.36. Що таке «коефіцієнт заповнення» для періодичної послідовності прямокутних імпульсів?

3.37. Що ми називаємо «меандром»?

3.38. Що таке «випадковий сигнал»?

3.39. Що таке «шумовий сигнал»?

3.40. Що таке «шумова завада»?

Задача 3.1. Випрямляч не пропускає від’ємні значення сигналу. На вхід випрямляча подали гармонічний сигнал з періодом 0,3 мс. Якою є тривалість імпульсів на його виході?

Розв‘язок:

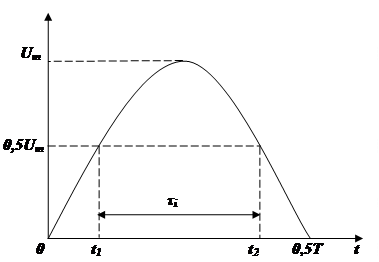
Очевидно, сигнал на виході випрямляча буде являти собою часову послідовність однополярних (додатної полярності) імпульсів з тим же періодом (Т = 0,3 мс). -Зобразимо на рису нку один з таких імпульсів. Виходячи із симетрії додатніх і від‘ємних півхвиль гармонічного сигналу, можна стверджувати, що

часова протяжність наявності додатної напруги на виході випрямляча складе 0,5Т, тобто, 0,15 мс. Відразу ж зауважимо, що цей часовий інтервал не є потрібною нам тривалістю імпульсу. Згідно з визначенням (див. матеріал лекції) тривалість імпульсу τ_i визначається по його половинному рівню, тобто, по рівню 0,5U_m, як це і зображено на рисунку. Як витікає з рисунку, τ_i = t₁ - t₂. Числові значення для t₁ і t₂ визначимо виходячи з того, що гармонічний сигнал є синусоїдальним сигналом. Таким чином, на нашому рисунку зображена додатня півхвиля синусоїди і той факт, що моменту часу t₁ відповідає значення синусоїди 0,5U_m, означає, що приріст фази ωt₁ складає π/6 рад або 30^о, бо саме Sin30^о = 0,5. виходячи з цього, можна записати: ωt₁ = π/6, звідки: 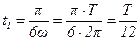. Як видно з рисунку, симетричний часовий інтервал 0,5Т - t₂ також дорівнює 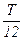. Звідки витікає, що . Знаючи t₁ і t₂, визначаємо щукану тривалість імпульсу: мс = 100 мкс.

Відповідь: τ_i = 100 мкс.

Задача 3.2. На щитовому розподілювачі електростанції є три вольтметри і кожен з них індикує напругу 380 В.

а) Що за напругу вони показують?

б) Яку форму має часова залежність миттєвого значення цієї напруги?

в) Чому дорівнює пікове значення цієї напруги?

г) Яким є миттєве значення цієї напруги?

д) Яким є розмах цієї напруги?

е) Чому дорівнює середнє значення цієї напруги?

є) Яку постійну складову має ця напруга?

ж) Чому дорівнює середньовипрямлене значення цієї напруги?

з) Яким є коефіцієнт амплітуди цієї напруги?

и) Чому дорівнює коефіцієнт форми цієї напруги?

Розв‘язок:

а) всі електротехнічні контрольно-вимірювальні прилади промислового та побутового призначень завжди показують середньоквадратичне значення змінної напруги, яка умовно позначається великою літерою U латинського алфавіту. Отже, U = 380 В. В промислових та побутових електромережах така напруга є гармонічною, тобто її миттєві значення здійснюють коливання за синусоїдальним законом. Для такої змінної напруги її середньоквадратичне значення називають ще діючим або ефективним.

Найпоширенішою у світі є трифазна система електричного енергопостачання. Вона складається із трьох ланцюгів, в кожному з яких діють змінні напруги однієї частоти, але зсунуті по фазі одна відносно одної на 1/3 періоду (кут зсуву φ=2π/3 рад = 120º). Окремий ланцюг такої системи коротко називають «фазою», а систему з трьох зсунутих по фазі змінних струмів – трифазним струмом. Лінія електропередачі такої системи енергопостачання є чотиридротовою: це три «фазні» дроти, що позначаються великими першими літерами латинського алфавіту («А», «В», «С») та ще один, четвертий, так званий «нульовий» (умовно позначається як «0») дріт. Цей нульовий дріт, як правило, «заземлюють» – так роблять з метою зменшення небезпеки ушкодження електричним струмом людей, що працюють з електроприладами – металеві конструкції цих приладів також «заземлюють».

Напруга між будь яким двома фазними дротами називається «лінійною» напругою U_Л (U_АВ, U_ВС, U_АС) а напруга між будь-яким фазним дротом і нульовим дротом називається «фазною» напругою U_Ф (U_А, U_В, U_С). Згідно з Європейським стандартом U_АВ = U_ВС = U_АС =380 В, а U_А = U_В = U_С =220 В. Співвідношення між лінійною і фазною напругами: U_Л = U_Ф. Таким чином, оператор за показами щитових вольтметрів контролює відповідність напруг трифазної мережі встановленому номіналу. Згідно з даними, наведеними в умові задачі, електростанція працює в номінальному режимі.

U U_m     0 T/4 T/2 T t U_p   -U_m  

Як правило, рухомі частини електромеханічних вимірювальних приладів, внаслідок своєї будови, є інерційними, а тому вони не в змозі адекватно відслідковувати миттєві зміни вимірюваних електричних величин. Покази таких приладів (наприклад, кут відхилення стрілки-покажчика вздовж шкали) є результатом деякою опосередкування – інтегрування – миттєвих значень вимірюваних величин. 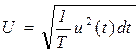Дійсно, середньоквадратична напруга U, яку показують щитові вольтметри, згадані в умові задачі, визначається як: , де u(t) – закон зміни миттєвого значення вимірюваної напруги з плином часу.

б,в,г,д) Як вже згадувалося у відповіді на попередній пункт, в побутових електромережах значення миттєвої напруги здійснює свої коливання за синусоїдальним законом (див.рисунок), а саме: 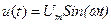, де U_т – пікове (амплітудне, максимальне) значення миттєвої напруги, В; ω = 2πf =

=– кутова частота осциляцій синусоїдальної напруги, рад/c; f – лінійна (циклічна) частота осциляцій синусоїдальної напруги, Гц; Т – період осциляцій синусоїдальної напруги, c; U_р = 2U_m – розмах напруги, В. Ді юче значення змінної напруги в електромережі U пов‘язане з її амплітудним значенням U_т через коефіцієнт амплітуди: К_А = U_т / U. як було сказано в лекційному курсі, для синусоїдального сигналу К_А =. Таким чином, в мережі з діючою (ефективною, середньоквадратичною) напругою 220 В максимальне (амплітудне, пікове) значення напруги складає: U_т = К_А U = ^.220 ≈ 311 В. А це означає, що розмах напруги в цій мережі складає: U_р = 2U_m ≈ 622 В.

е,є) Середнє значення цієї напруги U_ср або її постійна складова U₀ в силу симетрії осцилограми цієї напруги (див. рисунок у попередньому пункті) дорівнює нулю: протягом одного періоду напруги дія додатного півперіоду дорівнює очевидно є такою ж, як і дія від‘ємного півперіоду, а це означає, що в межах періоду вони взаємно зрівноважуються і їх сумарна дія є нульовою.

Доведемо це. Згідно з матеріалом лекції: . Підставимо в цю формулу вираз для гармонічної напруги і виконаємо операцію інтегрування:

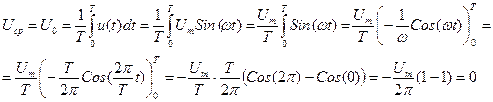
Це й потрібно було довести.

ж) Згідно з матеріалом лекції: 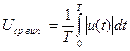. Слід підставити в цю формулу вираз для гармонічної напруги і виконати операцію інтегрування. Для спрощення цієї процедури, інтегрування проведемо в межах від 0 до 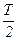, відповідно, опосередковуючи отриманий результат інтегрування також в межах півперіоду. Очевидно, що результат такого інтегрування буде таким же, як в загальному випадку:

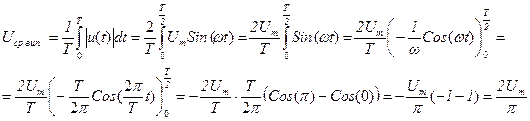
Таким чином, 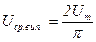і для побутової електромережі (U = ^.220 В) це складе: .

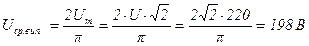з) Коефіцієнт амплітуди, як подано в матеріалах лекції, визначається таким: . Оскільки для синусоїдальної напруги 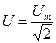, то, відповідно, .

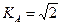и) За визначенням, коефіцієнт форми для змінної напруги визначається виразом: К_Ф = U / U_ср.вип. Оскільки, для синусоїдальної напруги 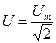, а 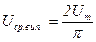, то, відповідно,

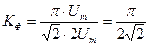
Задача 3.3. При визначенні за допомогою шалькових рівноплічних терезів маси проби водню вона була зрівноважена платиновими різновагами 50,00 та 25,00 г. Якою є маса проби водню, якщо маса колби, що вміщує цей водень, дорівнює 80,00 г? Дайте оцінку похибки такого зважування.

Розв‘язок:

    F₂   F₁ т_пл1 т_пл2 т_ск т_в   P₁P₂  

Причиною невідповідності мас об‘єктів, що врівноважуються в повітрі на різнобічних шальках терезів (див. рисунок), є несиметрія сил Архімеда, що діють на ці об‘єкти, які є вельми різними за своєю густиною – платина і скляна колба з воднем. Умовою рівноваги

терезів, очевидно, є рівність сил, що діють на кожну з шальок. Запишемо цю умову:

P₁ – F₁ = P₂ – F₂, (3.3.1.)

тут: P₁ = (т_пл1 + т_пл2)g – сумарна вага платинових різноваг; F₁ =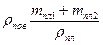 g – є силою Архімеда, що діє на платинові різноваги;

P₂ = (т_ск + т_в)g – сумарна вага скляної колби і проби водню, що знаходиться в ній; F₂= ρ_пов^.V_ск ^. g – сила Архімеда, що діє на скляну колбу з воднем.

Зробимо необхідні зауваження. Водень, як газ, що легший за повітря, «наливається знизу вгору» в колбу, перекинуту отвором вниз. Це означає, що тиск водню в колбі дорівнює зовнішньому атмосферному тиску повітря. Оскільки в умові задачі нічого не сказано про розміри та форму колби, то це нам дає певну волю вибору: для простоти розрахунків будемо вважати що колба має сферичну форму, а її об‘єм (V_ск 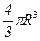^.= , де R – радіус сферичної скляної колби) приймемо таким, щоб умова задачі задовольнялася.

Враховуючи сказане, перепишемо рівняння (3.3.1.) у вигляді:

(т_пл1 + т_пл2)g –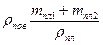 g = (т_ск + т_в)g – ρ_пов^.V_ск ^. g або: (3.3.2.)

т_пл1 + т_пл2 –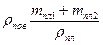= т_ск + т_в – ρ_пов 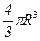. (3.3.3.)

в останньому рівнянні відомі всі величини, що входять до його складу, окрім двох: т_в і R. пов‘яжемо їх між собою: т_в = ρ_в V_ск = ρ_в 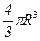, звідки: 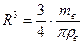. З урахуванням цього, вираз (3.3.3.) набуде вигляду:

т_пл1 + т_пл2 –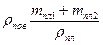= т_ск + т_в – ρ_пов^{. .} або: (3.3.4.)

Розв‘язавши рівняння (3.3.4.) відносно т_в , отримаємо:

т_в = 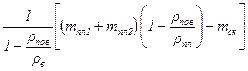(3.3.5.)

Обрахуємо за цим виразом шукану масу проби водню, взявши необхідні значення густин матеріалів із довідника. Числові значення величин підставляємо згідно з системою СІ.

т_в = =

= ≈ 3,75^.10^{-4 кг = 0,375 г = 375 мг.}

Отже, маса проби водню, визначена за даними умови задачі, складає 375 мг. Вважаємо, що не зайвим буде визначити об‘єм скляної колби, в якій міститься водень:

V_ск = .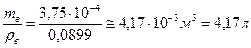

Визначимо також товщину колби d, беручи до уваги, що ця товщина є набагато меншою, ніж радіус сфери цієї ж колби. Запишемо очевидну рівність для об‘єму скла (V_c), з якого зроблена скляна сфера:

. (3.3.6.)

З цієї рівності визначимо:

Обрахована товщина оболонки скляної сфери складає 0,255мм, тобто, ця сфера є вельми ажурною, але все ж вона може бути реальною.

Дамо оцінку похибці такого зважування. Будемо розглядати описане в умові задачі зважування, як непрямі вимірювання маси водню, оскільки шуканий результат цих вимірювань є наслідком обрахунків. А тому і похибку таких непрямих вимірювань ми також будемо визначати розрахунковим шляхом.

Прологарифмуємо вираз (3.3.5.), з якого обчислювалася маса:

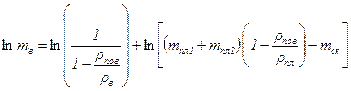. (3.3.7.)

Вважаючи, що ρ_вод << ρ_пов << ρ_пл, спростимо вираз (3.3.7.):

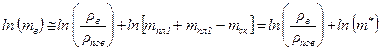. (3.3.8.)

Тепер продиференціюємо кожен член рівності, вважаючи при цьому, що кожен окремий член цієї рівності функціонально не залежить від інших членів цієї рівності:

(3.3.9.)

Замінюючи у виразі (3.3.9.) диференціали аргументів на їх прирости (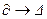), отримаємо шуканий вираз для відносної похибки вимірювання маси проби водню:

(3.3.10.)

Зауважимо, що на останньому кроці ми записали всі складові в правій частині рівності (3.3.9.), як арифметичну суму. Це ми зробили так для того, щоб врахувати найбільш несприятливий із можливих випадків поєднань відхилень окремих складових похибки.

Підставляючи в (3.3.10.) числові дані із умови задачі, враховуємо з якою точністю вони нам задані. Значення мас задані з точність до двох знаків після коми, тобто Δт ≤ 0,01 г. Значення густин речовин, які ми брали із довідників, для повітря обмежимо двома знаками після коми, тобто Δρ ≤ 0,01 кг/м³, а для водню – чотирма, тобто Δρ ≤ 0,0001 кг/м³. Тоді:

%

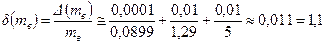Отримана таким чином величина відносної похибки визначення маси проби водню, згідно з даними із умови задачі, дозволяє вважати результати зважування задовільними.

Задача 3.4 (жарт). Якого смаку є протон? Відповідь обґрунтуйте.

Розв‘язок:

Протоном ми називаємо елементарну частинку матерії, що має одиничний позитивний елементарний заряд + е (е = - 1,6^.10^-19 Кл – заряд електрона). Протона прийнято позначати як р. Разом з нейтронами (п) протони складають ядра атомів. Найпростішим за своєю будовою, є ядро атома водню – найлегшого та найпоширенішого в природі елементу. Ядро цього атома утворене лише одним протоном. Таким чином, атом водню має таку «будову»: в центрі атома розташований протон, навколо якого рухається електрон. Своїм рухом електрон визначає розмір атома – діаметр атома водню складає приблизно 1 Ангстрем (1Å = 10^{-10 м), а маса атома практично вся зосереджена в його ядрі, а отже, визначається масою протона.}

Як відомо з хімії, молекули всіх кислот містять в своєму складі атоми водню, які енергетично пов‘язані з певними групами атомів, що мають загальну назву «кислотний залишок». Для простих мінеральних кислот, таких як соляна (НСl) чи плавикова (HF), «кислотним залишком» може бути всього один атом (Сl або F), а, наприклад, у сірчаної кислоти (Н₂SО₄), це вже цілий «комплекс» атомів – SО₄. молекули органічних кислот, як правило, ще складніші (винятком може бути хіба що НСООН – мурашина кислота).

Як видно вже з самої назви цих речовин, загальною відзнакою їх кислот є та, що всі вони на смак «кислі». Зрозуміло, що пробувати «на язик» концентровані кислоти ні в якому разі не можна! Відчайдух гарантовано отримає лише важкі травми ротової порожнини, як наслідок так званого «хімічного опіку». Реально до рота можна взяти «на пробу» лише дуже сильно розбавлений водою розчин кислоти – образно кажучи: коли на відро чистої води припадає крапля кислоти.

А чому всі кислоти «кислі»? Справа в тім, що перебуваючи у водному розчині (а саме в такому вигляді кислоти і потрапляють до нашого рота) молекули всіх кислот дисоціюють (розділяються, розпадаються) там на позитивно заряджені іони водню і на негативно заряджені іони кислотного залишку, наприклад: НСl → Н⁺ + Сl^–, Н₂SО₄ → Н⁺ + Н⁺ + SО₄^{– –}, НСООН → Н⁺ + СООН^– і т.п. Як видно з цих прикладів, спільною характерною ознакою для розчинів усіх кислот є наявність в них позитивних іонів водню. очевидно, саме завдяки цьому фактору – дії іонів водню на смакові рецептори язика людини – у нас і формується відчуття, що речовина в нашому роті є «кислою».

А що таке «позитивно заряджений іон водню»? Очевидно, це є атом водню, що втратив свого єдиного електрона – він (електрон) перейшов до кислотного залишку. Що ж тоді залишається від атома водню, або чим же тоді є насправді «позитивно заряджений іон водню»? Так, дійсно, це і є протон. Таким чином, саме наявність вільних протонів у розчинах усіх кислот і робить ці розчини кислими на смак. Отже, виходячи із всього сказаного можна так відповісти на поставлене в задачі запитання: протон кислий на смак.

Задача 3.5.

Всі ми спостерігали, що коли Сонце і Місяць перебувають поблизу лінії горизонту (під час їх сходу та заходу), то їх розміри видаються нам значно більшими, ніж тоді коли вони перебувають посеред неба. Разом з тим, відомо, що це є зоровою оманою – прямі вимірювання показують, що кутові розміри і Сонця, і Місяця є незмінними і не залежать від розташування цих світил на небосхилі. В чому ви вбачаєте причину цієї зорової омани? Відповідь обґрунтувати.

Розв‘язок:

Зрозуміло, що відстань від людини, яка перебуває на поверхні Землі, до небесного світила не залежить від його розташування на небосхилі. Вся причина в тому, що оцінювана нашою свідомістю видима нами «відстань до неба» суб‘єктивно є різною для різних «ділянок неба». Ті «ділянки неба», що «межують з горизонтом», видаються нам віддаленими від нас настільки ж, як і сама ліня горизонту. А чи «далеко» від нас розташована лінія горизонту? Цю відстань легко розрахувати, скориставшись рис.1, де півколом з радіусом R зобра-

жена поверхня нашої Землі, на полюсі якої стоїть людина (коротенька жирна рисочка), що має зріст h і дивиться на край горизонту (лінія її погляду, очевидно, є дотичною до поверхні Землі і перпендикулярною до радіусу Землі, проведеного до лінії горизонту). Відстань від людини до горизонту l визначимо із

теореми Піфагора: 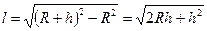або, враховуючи, що h << R, . Приймаючи зріст людини h = 2 м, а радіус Землі R = 6400 км = 6,4^.10⁶ м, отримаємо:

, тобто, лінія горизонту є не такою вже й віддаленою від нас. Суб‘єктивно ж оцінювана людиною, тобто, «видима» нею, відстань Н до небесного купола в напрямку зеніту, видається дещо меншою, лише ≈ 3,5 км. Таким чином, небесний

купол, який ми бачимо над поверхнею землі, видається нам не сферичним, як слід було б очікувати, а еліпсоїдальним: дещо «приплюснутим» в напрямку зеніту і трохи «розтягнутим» в напрямку горизонту, як це показано на рис.2.

Відомо, що видимий людиною з поверхні Землі кутовий розмір і Сонця, і Місяця Δφ складає ≈ 0,5′′. Враховуючи ж особливості сприйняття людиною форми небесного куполу над її головою, один і той же конус променів, що йдуть від країв диску світила до нашого ока, «вирізає» на видимому небесному куполі різні за площею поверхні, залежно від того, як високо над горизонтом перебуває світило. Зрозуміло, що з точки зору людини, яка перебуває на земній поверхні в центрі еліпсоїду видимого нею небосхилу (в точці О, див. рис.2), ця площа буде найбільшою тоді, коли світило перебуває на лінії горизонту і найменшою – коли воно досягає на небосхилі свого найвищого положення над горизонтом (гранично – коли світило перебуває зеніті).

Дата добавления: 2014-01-07