Задачі до розділу 3.3

Задача 3.3.1

Уздовж бензоколонки проїжджає 60% легкових автомобілів і 40% вантажних автомобілів. Ймовірність того, що заправлятиметься вантажна машина 0,1, для легкової машини ця ймовірність дорівнює 0,2. До бензоколонки під’їхала машина для заправки. Знайти ймовірність того, що це буде вантажна машина.

Рішення

Подія А – до бензоколонки під’їхала для заправки машина.

Можна висунути дві гіпотези:

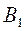- машина легкова;

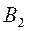- машина вантажна.

Тоді, , .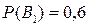

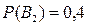Умовна ймовірність того, що заправлятиметься легкова машина:

.

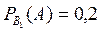Умовна ймовірність того, що заправлятиметься вантажна машина:

.

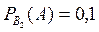Ймовірність того, що до бензоколонки під’їхала для заправки машина, знаходимо за формулою повної ймовірності

,

.

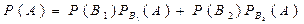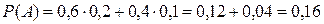Шукану ймовірність, що для заправки під’їде вантажна машина, знайдемо за формулою Бейєса

,

.

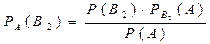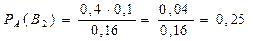Задача 3.3.2

У крамниці для продажу є 15 рушниць, з яких 5 з оптичним прицілом. Ймовірність того, що стрілець влучить у мішень з рушниці з оптичним прицілом 0,95, для рушниці без оптичного прицілу ця ймовірність дорівнює 0,8. Стрілець влучив у мішень з навмання купленої рушниці. Знайти ймовірність того, що стрілець стріляв з рушниці без оптичного прицілу.

Задача 3.3.3

У наявності є три партії деталей по 30 деталей в кожній. Число стандартних деталей у першій, другій і третій партіях відповідно дорівнює 20, 15 і 10. Із навмання обраної партії навмання вилучено деталь, яка виявилася стандартною. Знайти ймовірність того, що деталь було вилучено із третьої партії.

Розділ 3.4. Завдання до заняття 3

Теоретичні питання до розділу 3

1. Сформулювати теорему про ймовірність появи хоча б однієї події.

2. Які події утворюють повну групу?

3. Сформулювати теорему про повну ймовірність.

4. Що ви розумієте під терміном „гіпотеза”.

5. Записати формулу Бейєса та пояснити її складові.

Розділ 4.1. Формула Бернуллі

Нехай виконується п незалежних випробувань, в кожному з яких подія А може з’явитися або ні. Ймовірність появи події А в кожному випробуванні однакова і дорівнює р. Відповідно, ймовірність того, що подія А не з’явиться в кожному випробуванні також постійна і дорівнює .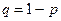

Необхідно визначити ймовірність того, що при п випробуваннях подія А з’явиться рівно 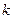раз, тобто не з’явиться 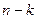раз, причому не має значення у якій послідовності з’являється подія А. Наприклад, подія А з’явиться 3 рази у 4-х випробуваннях: .

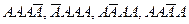Позначимо шукану ймовірність ймовірність однієї складної події, яка полягає в тому, що в п випробуваннях подія А з’явиться рівно 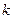раз і не з’явиться 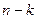раз, тоді за теоремою множення ймовірностей незалежних подій вона дорівнює 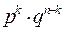. Таких складних подій може бути стільки, скільки можна скласти сполучень з п елементів по k елементах, тобто 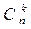. Оскільки ці складні події несумісні, тому за теоремою додавання ймовірностей несумісних подій, шукана ймовірність дорівнює сумі ймовірностей всіх можливих складних подій. Оскільки всі складові однакові, то шукана ймовірність дорівнює ймовірності однієї складної події, помноженої на їх кількість.

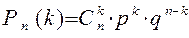, (4.1)

або

.

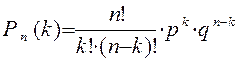Приклад:

Ймовірність того, що витрати електроенергії впродовж однієї доби не перевищать встановленої норми, дорівнює 0,8. Знайти ймовірність того, що найближчі 6 діб витрати електроенергії протягом 4 будь-яких діб не перевищать норми.

Дата добавления: 2014-01-07