Задачі до розділу 6.3

Задача 6.3.1

Знайти математичне сподівання кількості очок, що випадають при киданні кубика.

Рішення

Перелічимо всі можливі значення дискретної випадкової величини Х – кількості очок, що випадають при киданні кубика Х: {1, 2, 3, 4, 5, 6}. Складемо закон розподілу ймовірностей дискретної випадкової величини Х.. Ймовірності випадання будь-якої з шести можливих варіантів кількості очок однакові

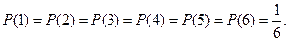
Х
Р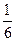

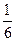
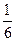
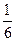
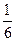
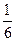
За формулою (6.2) знайдемо математичне сподівання дискретної випадкової величини Х

Задача 6.3.2

Нехай щодобові витрати на обслуговування і рекламу товару на підприємстві складають у середньому 100 грн., а число продаж протягом доби підпорядковується наступному закону розподілу

Х
Р	0,05	0,10	0,20	0,30	0,15	0,10	0,05	0,03	0,02

Знайти математичне сподівання щодобового прибутку при ціні на одиницю товару 1000 грн.

Рішення.

За формулою (6.2) знайдемо математичне сподівання дискретної випадкової величини Х

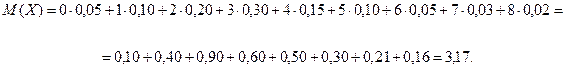
Щодобовий прибуток можна обрахувати за формулою

П=(1000Х-100), грн.

Шукана характеристика М(П) знаходиться за допомогою властивостей математичного сподівання

М(П)=М(1000Х-100)=1000М(Х)-100=1000·3,17-100=3170-100=3070 грн.

Задача 6.3.3

Знайти математичне сподівання дискретної випадкової величини, яка задана законом розподілу:

а)

Х	-4	-1
Р	0,1	0,2	0,1	0,3	0,1	0,2

б)

Х
Р	0,2	0,3	0,1	0,2	0,2

Задача 6.3.4

Знайти математичне сподівання випадкової величини Z, якщо відомі математичні сподівання Х і У:

а) Z=X+2У, М(Х)=4; М(У)=7;

б) Z=3X+4У, М(Х)=3; М(У)=5;

в) Z=X-2У+5, М(Х)=2; М(У)=6.

Розділ 6.4. Завдання до заняття 6

Теоретичні питання до заняття 6

1. Дати означення дискретної випадкової величини.

2. Дати означення неперервної випадкової величини.

3. Дати означення закону розподілу дискретної випадкової величини.

4. Дати означення математичного сподівання.

5. Перелічити властивості математичного сподівання.

Дата добавления: 2014-01-07