Рішення. Обсяг генеральної сукупності , тоді за формулою (12.2) заняття 12 знайдемо середню арифметичну

Обсяг генеральної сукупності 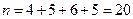, тоді за формулою (12.2) заняття 12 знайдемо середню арифметичну

Для знаходження середнього квадрата ознаки складемо таблицю

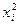
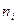
Тоді за формулою (12.7) заняття 12 знайдемо квадрат середньої

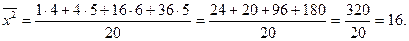
Враховуючи, що , застосуємо формулу (12.6) заняття 12 для знаходження дисперсії

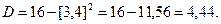
За формулою (12.5) заняття 12 знайдемо середнє квадратичне відхилення

.

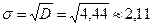Тоді за формулою (13.1) знайдемо коефіцієнт варіації

.

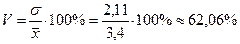Розділ 13.2. Медіана варіаційного ряду

Означення: Медіаною варіаційного ряду називається варіанта, яка припадає на середину варіаційного ряду.

Для дискретного розподілу медіана знаходиться досить просто. Можуть мати місце два випадки.

1). Обсяг сукупності є непарним числом :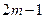

.

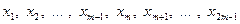Медіаною цього розподілу є варіанта 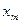, тому що до неї і після неї знаходиться по 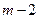варіанти, тобто

.

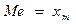2) Обсяг сукупності є парним числом, тоді за медіану приймають напівсуми варіант, що знаходяться в середині ряду

.

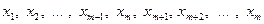Медіана цього розподілу є напівсумою варіант 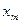і 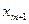, тому що до неї і після неї знаходиться по 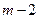варіанти, тобто

.

Для неперервного розподілу, медіану можна обчислити за формулою

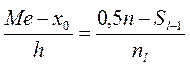, (13.2)

де 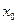- початкове значення медіанного інтервалу; 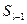- накопичена частота інтервалу, який знаходиться перед медіанним інтервалом; 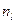- частота медіанного інтервалу; - довжина медіанного інтервалу (шаг); 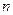- обсяг сукупності.

Приклад:

Дано розподіл 49 промислових підприємств за швидкістю обігових коштів. Знайти медіану даного розподілу.

Швидкість обігу, Кількість

в днях, 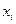підприємств

20 – 30 8

30 – 40 11

40 – 50 16

50 – 60 9

60 – 70 5

Всього: 49

Рішення

Знайдемо середину ряду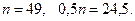

Розділимо вибірку на дві частини: меншу за 24,5 і більшу за 24,5.

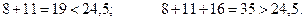
Значить медіанний інтервал (40 – 50). Тоді: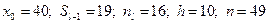

За формулою (13.2) обчислимо медіану

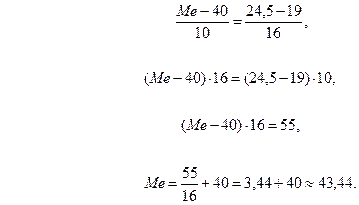
Розділ 13.3. Мода варіаційного ряду

Означення: Модою варіаційного ряду називається варіанта, що найбільш часто зустрічається, тобто має найбільшу частоту.

Як видно з означення, при дискретному розподілі знаходження значення моди не потребує будь-яких складних обчислень. Із статистичного розподілу обирається найбільша частота і варіанта, яка їй відповідає і є модою.

Для неперервного розподілу мода обчислюється за формулою

(13.3)

де 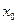- початкове значення модального інтервалу; - довжина модального інтервалу (шаг); 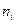- частота модального інтервалу; 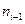- частота інтервалу, який знаходиться перед модальним; - частота інтервалу, який знаходиться після модального.

Приклад:

Для попереднього прикладу про розподіл 49 промислових підприємств за швидкістю обігових коштів, знайти моду даного розподілу.

Рішення

За формулою (13.3) обчислимо моду статистичного ряду. Оскільки 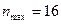, то інтервал (40 – 50) є модальним.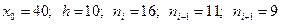

Ляпунов Олександр Михайлович (6.06.1857 – 3.11.1918 рр.) – російський математик і механік, професор, академік. Зробив важливий внесок до теорії ймовірностей, дав просте і строге доведення центральної граничної теореми у більш загальній формі, для цього розробив оригінальний метод характеристичних функцій, який широко застосовується у сучасній теорії ймовірностей.

Розділ 13.4. Асиметрія і ексцес

Для введення таких числових характеристик, як асиметрія і ексцес, необхідно спочатку ввести поняття моментів варіаційного ряду.

Дата добавления: 2014-01-07