Нормального розподілу

Нехай кількісна ознака Х генеральної сукупності розподілена нормально, причому середнє квадратичне відхилення генеральної сукупності не відоме. Необхідно оцінити невідоме математичне сподівання 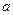за допомогою довірчих інтервалів. За даними вибірки можна побудувати випадкову величину, яка має розподіл Ст’юдента з 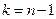степенями свободи

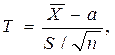
де 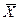- вибіркова середня; 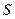- виправлене середнє квадратичне відхилення; 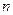- обсяг вибірки.

Щільність розподілу Ст’юдента має вигляд

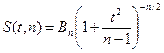, де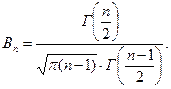

Ми бачимо, що розподіл Ст’юдента визначається параметром п – обсягом вибірки, що теж саме, що й числом степеней свободи 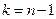і не залежить від параметрів 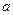і .

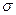Знайдемо надійність параметра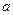

.

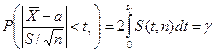Шляхом елементарних перетворень, перейдемо до подвійної нерівності

.

Користуючись розподілом Ст’юдента, знайдемо довірчий інтервал, що покриває невідомий параметр 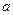з надійністю

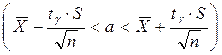. (14.8)

За таблицею критичних точок розподілу Ст’юдента за заданими 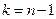і , можна знайти .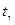

Приклад:

Кількісна ознака Х генеральної сукупності розподілена нормально. За вибіркою обсягу 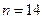знайдено середню вибіркову 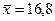і виправлене середнє квадратичне відхилення 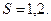Оцінити невідоме математичне сподівання за допомогою довірчого інтервалу з надійністю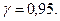

Рішення

За таблицею критичних точок розподілу Ст’юдента на перетині числа степеней свободи 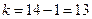і 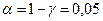(двостороння критична область), можна знайти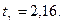

Тоді, за формулою (14.8) маємо

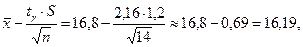
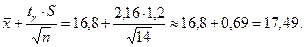
Таким чином, з надійністю 0,95 невідомий параметр 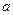покриває довірчий інтервал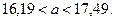

Довірчий інтервал для оцінки середнього квадратичного відхилення

нормального розподілу

Нехай кількісна ознака Х генеральної сукупності розподілена нормально. Необхідно оцінити невідоме генеральне середнє квадратичне відхилення 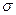за виправленим середнім квадратичним відхиленням 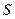, тобто знайти довірчий інтервал, що покриває параметр 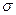з заданою надійністю . Для цього необхідне виконання співвідношення

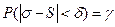
або

.

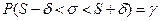Винесемо 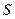за дужки і зробимо заміну 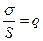, після чого одержимо

.

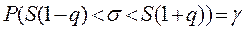Тоді довірчий інтервал можна виразити за формулою

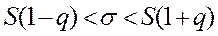. (14.9)

На практиці, для знаходження 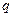користуються таблицею значень, що наведена нижче. Але формула (14.9) справедлива при .

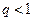Таблиця значень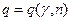

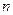
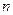
0,95	0,99	0,999	0,95	0,99	0,999
	1,37	2,67	5,64		0,37	0,58	0,88
	1,09	2,01	3,88		0,32	0,49	0,73
	0,92	1,62	2,98		0.28	0.43	0,63
	0,80	1,38	2,42		0,26	0,38	0,56
	0,71	1,20	2,06		0.24	0,35	0,50
	0,65	1,08	1,80		0,22	0,32	0,46
	0,59	0,98	1,60		0,21	0,30	0,43
	0,55	0,90	1,45		0,188	0,269	0,38
	0,52	0,83	1,33		0,174	0,245	0.34
	0,48	0,78	1,23		0,161	0.226	0,31
	0,46	0,73	1,15		0,151	0,211	0,29
	0,44	0,70	1,07		0,143	0,198	0,27
	0,42	0,66	1,01		0,115	0,160	0,211
	0,40	0,63	0,96		0,099	0,136	0,185
	0.39	0,60	0,92		0,089	0,120	0,162

Якщо 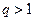, тоді нерівність (14.9) набуде вигляду (враховуємо, що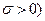

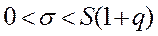. (14.10)

Приклад:

Кількісна ознака Х генеральної сукупності розподілена нормально. За вибіркою обсягу 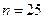знайдено виправлене середнє квадратичне відхилення 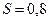. Знайти довірчий інтервал, що покриває генеральне середнє квадратичне відхилення 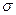з надійністю 0,95.

Рішення

За таблицею значень 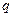за даними 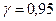і 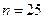знайдемо 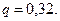Тоді за формулою (14.9)

,

.

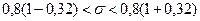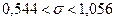Таким чином, довірчий інтервал 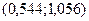покриває невідомий параметр генеральної сукупності 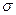з надійністю 0,95.

Приклад:

Кількісна ознака Х генеральної сукупності розподілена нормально. За вибіркою обсягу 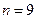знайдено виправлене середнє квадратичне відхилення 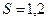. Знайти довірчий інтервал, що покриває генеральне середнє квадратичне відхилення 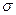з надійністю 0,99.

Рішення

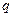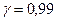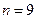За таблицею значень за даними і знайдемо Тоді за формулою (14.10)

,

.

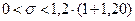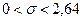Таким чином, довірчий інтервал 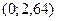покриває невідомий параметр генеральної сукупності 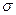з надійністю 0,99.

Дата добавления: 2014-01-07