Сполучення:

Перестановки:.

Класичне означення ймовірності появи події:.

Основні теореми і формули

Розміщення: .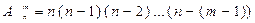

Теорема додавання ймовірностей несумісних подій: .

Ймовірність повної групи подій:

Сума ймовірностей протилежних подій: .

Ймовірність сумісної появи двох подій: .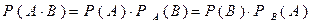

Ймовірність сумісної появи двох незалежних подій: .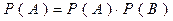

Ймовірність появи однієї з двох сумісних подій: .

Ймовірність появи хоча б однієї з подій: .

Формула повної ймовірності: .

Формули Бейєса: .

Формула Бернуллі: .

Локальна теорема Лапласа: 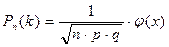, де .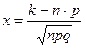

Інтегральна теорема Лапласа: , де .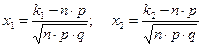

Формула Пуассона: , де .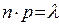

Математичне сподіваннядискретної випадкової величини:

.

Дисперсія дискретної випадкової величини: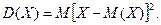

.

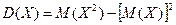Середнє квадратичне відхилення: .

Функція розподілу (інтегральна функція розподілу): .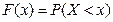

Ймовірність того, що випадкова величина 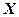прийме значення із проміжку : .

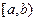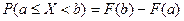Диференціальна функція розподілу: .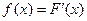

Ймовірність того, що неперервна випадкова величина прийме значення з інтервалу :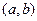

Зв’язок між інтегральною і диференціальною функціями розподілу:

Математичне сподівання неперервної випадкової величини: .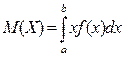

Дисперсія неперервної випадкової величини: ,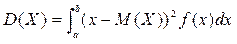

.

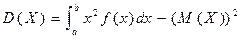Математичне сподівання при біноміальному законі розподілу: .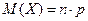

Дисперсія при біноміальному законі розподілу: .

Рівномірний розподіл ймовірності: .

Нормальний закон розподілу: .

Ймовірність попадання неперервної випадкової величини, розподіленої нормально, у заданий інтервал: .

Емпірична функція розподілу: .

Середня арифметична: ,

.

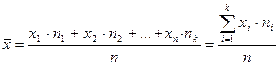Дисперсія: ,

.

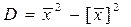
Коефіцієнт варіації: .

Медіана при неперервному розподілі: .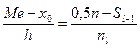

Мода при неперервному розподілі:

Коефіцієнт асиметрії: .

Ексцес або коефіцієнт крутості: .

Метод добутків: ,

.

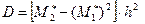Поправка Бесселя: .

Виправлена дисперсія:

Виправлене середнє квадратичне відхилення:

Довірчий інтервал для оцінки математичного сподівання: .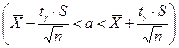

Довірчий інтервал для оцінки середнього квадратичного відхилення: .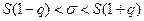

Перевірка гіпотези про рівність дисперсій двох генеральних сукупностей:

, .

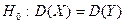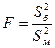1. , , , , .

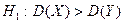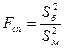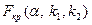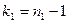Якщо 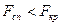, тоді немає підстав відкидати нульову гіпотезу. Якщо 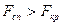, тоді нульову гіпотезу відкидаємо.

2. , , , , .

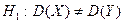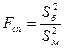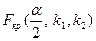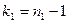Якщо 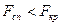, тоді немає підстав відкидати нульову гіпотезу. Якщо 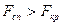, тоді нульову гіпотезу відкидаємо.

Перевірка гіпотези про нормальний розподіл генеральної сукупності. (Критерій згоди 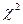-Пірсона): , , ,

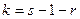Якщо 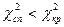, тоді немає підстав відкидати нульову гіпотезу. Якщо 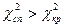, тоді нульову гіпотезу відкидають.

Методика обчислення теоретичних частот у припущенні нормального розподілу: ,, , .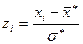

Метод найменших квадратів: .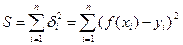

Рівняння прямої: .

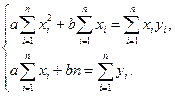Рівняння параболи: , .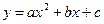

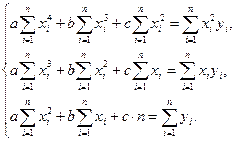Рівняння гіперболи: , , .

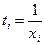Рівняння показникової функції: , , .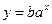

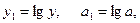
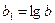Рівняння прямої лінії по згрупованим даним: .

Вибірковий коефіцієнт кореляції: .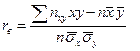

Дата добавления: 2014-01-07