Обмеження на функції вибору

Аксіома наслідування (H):

X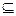^’XC (X^’) C 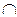(X) X^’.

Зміст цієї аксіоми зводиться до вимоги, щоб у вибір на підмножині X ^’ увійшли всі ті альтернативи із X^’, котрі входили у вибір на X.

Аксіома згоди (C):

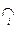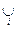C (X _i) C ( X).

Це означає, що у вибір із об’єднання множин обов’язково мусять входити альтернативи, що являється загальними для виборів з усіх множин.

Виявляється, що спільне підпорядкування функції вибору аксіомам Н та С дає описаний на мові бінарних відношень вибір.

Аксіома відкидання (O):

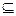C (X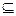) XX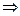C (X^’) C (X).

Це означає, що якщо відкинути довільну частину альтернатив, то вибір на множині, що залишилася, не зміниться; тому дану аксіому називається також умовою незалежності від відкинутих альтернатив.

Спільне накладання на вибір аксіом Н, С та О приводить до випадку вибору паретовської множини.

Аксіома Плота (KC):

C (X 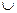X) = C (C (X₁) 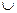C (X₂)).

Це відображає вимоги, що накладаються при багатоступеневих виборах, коли вважається, наприклад, що визначити чемпіона світу можна шляхом змагань між чемпіонами країн і результат буде тим же, якщо змагатися будуть не тільки чемпіони. Тому цю аксіому називається ще умовою незалежності від шляху. Функції вибору, що задовольняють їй, називається квазі суматорними.

Аксіома переваги (П):

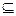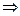X^’X C (X) 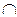X^’ = C (X^’).

Вона вимагає, щоби при звужені множини альтернатив у виборі залишилися лише ті альтернативи, котрі входили у вибір раніше.

У суспільстві одноособове прийняття рішення є не єдиною формою вибору. „Розум – добре, а два – краще”, говорить приказка, що має на увазі випадок, коли двоє з однаковими намірами намагаються знайти гарний вибір.

Дата добавления: 2014-01-07