Парадокси голосування

Наступна особливість правила голосування – це можливість відмови від вибору із-за недосягнення більшості, що вимагається. Здавалося б, якщо виключити таку можливість, то можна забезпечити прийняття рішення у довільних випадках. Наприклад, три експерти більшістю голосів вирішують питання, яка з двох альтернатив буде переважаючою. При такій постановці питання вони дійсно не можуть не зробити вибір. Однак тут приходять до ще одної особливості правил голосування - його не транзитивності.

Нехай, наприклад, кожна із трьох груп законодавців, які створюють більшість лише попарно, висунула свій варіант законопроекту: a, b та c. Щоби гарантувати більшість на кожному кроці процедури, альтернативи представляються попарно. Кожна сторона керується при цьому своїм набором переваг. Нехай це відповідно послідовності (a > b > c), (b > c > a) та (c > a > b).

При голосуванні по парі (a, b) в результаті отримують два голоси проти одного: a > b; по парі (b, c) маємо b > c; по парі (c, a) маємо c > a. Голосування більшістю не привело до з’ясування „“загально визнаного” порядку альтернатив: a > b > c > a. У випадку ж застосування процедури, при якій після розгляду чергової пари альтернатива, що була відхилена, замінюється новою, остаточно прийняте рішення залежить від порядку представлення альтернатив: при порядку (a, b, c) вибирається c; при порядку (b, c, a) вибір зупиняється на a; при порядку (a, c, b) – на b. Якщо таким чином прийняти законопроект, то чию думку він буде відображати – більшості чи організатора голосування? Таке рішення не відповідає ідеалу погодженого групового вибору.

Причина даного парадоксу не транзитивності групового вибору полягає у циклічності сукупності вихідних індивідуальних переваг. Однак, це лише частковий приклад більш загального явища, що має назву парадоксу Ерроу (або теореми про неможливість).

Із всіляких функцій F індивідуальних виборів R₁,..., R_n виділяють ті, котрі відповідають вимогам, що виражають розуміння того, який вибір можна вважати погодженим. Окрім формальних вимог:

1) „ n 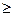2”, „число альтернатив 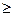3”, „ F визначено для довільних ”;

істотно також вимагати, щоби:

2) якщо у результаті групового вибору перевагу було віддано альтернативі x, то це рішення не повинно змінитися, якщо хто-небудь із експертів, хто раніше відкинув x, змінив свою перевагу в його користь (умова монотонності);

3) якщо зміни індивідуальних переваг не торкнулися конкретних альтернатив, то у новому груповому впорядкуванні порядок цих альтернатив не повинен змінюватися (умова незалежності незв’язаних альтернатив);

4) для довільної пари альтернатив x та y існує такий набір індивідуальних переваг, для котрого F (R₁,..., R_n) = (x > y) (умова суверенності; без неї можливе нав’язування y незалежно від порядку переваг індивідуумів);

5) не повинно бути такої особи, для якої із її переваги x > y (при довільних x та y) витікає, що F (R₁,..., R_n) = (x > y) незалежно від переваг других осіб (умова відсутності диктаторів).

Парадокс Ерроу полягає у тому, що перші чотири умови суперечать п’ятій; не існує правила F, що задовольняє всім п’ятьом вимогам. Аналіз причин такого наслідку із таких невинних на вид припущень показує, що основну роль грає можливість циклічних множин ранжирування, що характерна для бінарних відношень, котрі задовольняють умові 3.

Не транзитивність мажоритарних відношень може проявлятися і в інших неочікуваних формах. Розглянемо задачу: нехай кожний із n суб’єктів має свою долю a_i загального ресурсу a = a_i. Вектор 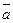= (a₁ ,..., a_n) назвемо станом системи. Другий стан = (b₁,..., b_n) з точки зору i -го суб’єкта гірше 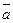, якщо a_i 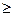b_i. Будемо виконувати перерозподіл ресурсів на основі дуже сильної більшості: система перейде із 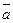в , якщо стан не гірше 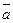для всіх, окрім одного (це так зване „тотально-мажоритарне правило”). Послідовність станів 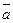₁, 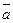₂,..., 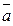_k називають тотально-мажоритарним шляхом із 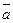₁ у 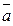_k, якщо переходом у черговий стан задоволені всі учасники, окрім того, чий ресурс в даний момент перерозподіляється. Нехай тепер задані два довільних стани системи 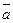та . При яких умовах існує тотально-мажоритарний шлях із 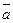у ? З’ясовується, що такий шлях існує завжди. Знову маємо справу з парадоксом: можливі довільні перерозподіли і всі вони виражають думку „всього суспільства”, окрім одного суб’єкта (правда, ці незгодні на різних етапах різні).

Задачі групового вибору часто все ж можуть бути розв’язаними. По-перше, у ряді випадків циклічні ранжирування можуть бути відсутніми, або вони не охоплюють „найбільш важливі альтернативи”, або приймаються засоби по їх виявленню та усуненню. По-друге, в багатьох випадках „диктаторський” принцип погодження є прийнятним. Це ілюструється прикладом оптимізації по „головному” із декількох критеріїв. В інших випадках це єдиний можливий принцип (наприклад, єдиноначальність в армії). По-третє, перехід (коли це можливо) до використання єдиної числової, а не порядкових індивідуальних шкал переваг, може взагалі анулювати проблему транзитивності. По-четверте, у реальних ситуаціях мажоритарні правила застосовуються у комбінації з другими правилами, так що, організувавши, наприклад, коаліцію, групи суб’єктів можуть блокувати голосування.

Тут приходимо ще до одної особливості голосування, яку належить мати на увазі. Мова йде про втручання коаліцій в механізм голосування, що фактично змінює його характер. Наприклад, при багатокроковому голосуванні по правилу більшості коаліція, що знаходиться у меншості, може добитися прийняття свого рішення.

2:1

4:5

8:19

Рис. 20. Ілюстрація парадоксу багатокрокового голосування при наявності коаліції

На Рис.20 зображено голосування по три більшістю у 2 / 3 на кожному кроці. Видно, що вже на другому кроці меншість може нав’язати свою думку більшості. Якщо число кроків не обмежувати, то теоретично меншість, що перемагає таким чином, може бути скільки завгодно малою. Те, що при багатокроковому голосуванні може перемогти кандидат, який не набрав дійсної більшості голосів, має місце й у дійсності.

6.3. Вибір та відбір

Досі мова йшла про процедури одноразового вибору. Навіть тоді, коли доводилося виконувати вибір у декілька етапів (багатокритеріальна оптимізація, колективний вибір тощо), це були етапи проміжні, підготовчі перед останнім, остаточним вибором.

Однак можливі ситуації коли вибір повторюється багатократно, причому кожний наступний крок виконується у відмінних від попередніх умовах. Це придає динаміку самому процесу вибору та його наслідкам. Конкретний характер змін, що відбуваються при цьому, залежить від багатьох факторів: самої природи множини альтернатив, ступеня впливу попереднього вибору на наступний, від того, наскільки та як саме враховуються зміни, що відбулися на черговому кроці вибору, тощо.

Найбільш докладно вивчені процеси прийняття статистичних рішень із адаптацією, тобто із зворотним зв’язком по рішенням, що прийняті на попередніх кроках. Прикладом можуть служити радіолокаційні станції, що постійно ведуть огляд заданої зони, накопичують інформацію про обстановку у зоні огляду і використовують її при опрацюванні прийнятих сигналів для виявлення цілей.

Другий приклад процесів багатократного вибору дає природний відбір. Своєрідність таких процесів вивчається теорією еволюції та математичною біологією.

Основний інтерес являють процеси свідомого вибору, тому, звертаючись до багатократного вибору, приходять до задач цілеспрямованого багатократного вибору, тобто штучного відбору, селекції. Як показали деякі дослідження, тенденції, що виникають у ході селекції, дуже залежать від конкретних способів формування та поповнення відбірних („елітних”) груп. Це треба мати на увазі при комплектації довільних груп елементів, у чомусь кращих, ніж решта: у промисловості – при виготовленні високосортної продукції; у сільському господарстві – при виводі високопродуктивних порід тварин та сортів рослин; в управлінській діяльності – при комплектації груп виконавців відповідальних справ тощо.

Наводимо схему, на якій зображені всі згадані у даному розділі задачі вибору, вказана їх загальність та різниця у ієрархічній класифікації.

адаптація по

розв’язку

селекція

голосування ігри з природою

експертний ігри із супротивником

людино-машиннийнаростаючий конфлікт

Дата добавления: 2014-01-07