Способи задання відношень

Означення 2.8. Розглянемо відношення RÍA´B. Нехай елемент a_iÎA. Перерізом відношення А за елементом a_i називається множина елементів b з В, для яких пара (a_i,b)ÎR:

R(a_i) = {bÎB | (a_i,b)ÎR}.

Множину всіх перерізів відношення R називають фактором-множиною множини B за відношенням R і позначають B/R. Вона повністю визначає відношення R.

Наприклад, нехай A={1,2,3}, B={2,3,4,5,6}. Відношення R = {(1,2), (1,4), (2,3), (3,3), (3,6)}. Очевидно, R(1) = {2,4}, R(2) = {3}, R(3) = {3,6}. Множина {R(1), R(2), R(3)} є фактор-множиною B/R.

Об’єднання перерізів за елементами деякої підмножини CÍA є перерізом R(C) відношення R за підмножиною С, тобто

.

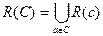Так для C={1,2}, маємо R(C) = {2,3,4} = R(1)ÈR(2).

З попереднього зрозуміло, що відношення може бути подане за допомогою фактор-множини. Розглянемо ще два способи подання скінченого бінарного відношення: за допомогою матриці та графа.

Матричний спосіб ґрунтується на поданні відношення RÍA´B відповідною йому прямокутною таблицею (матрицею), що складається з нулів та одиниць, де рядки – перші координати, а стовпці – другі, причому на перетині і-го рядка і j-го стовпця буде 1, якщо виконується співвідношення a_iRb_j, або 0 – якщо воно не виконується.

Для наведеного вище відношення матриця буде мати такий вигляд:

Матриця повного (універсального) відношення – це квадратна матриця, що складається лише з одиниць. Матриця тотожного (діагонального) відношення – це квадратна матриця, яка складається з нулів та одиниць по головній діагоналі. Матриця порожнього відношення – це квадратна матриця, що складається лише з нулів.

Відношення RÍA´B можна також зображати за допомогою орієнтованого графа. Елементи множин А та В зображаються точками на площині (вершини), а впорядковані пари – лінією зі стрілкою (дуги), яка направлена від a до b, якщо aRb.

Для наведеного вище відношення граф буде мати наступний вигляд:

Рис 2.1. Приклад представлення відношення за допомогою графа.

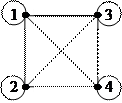
Граф бінарного відношення – це дводольний граф. Відношення в А зображується графом із вершинами, що відповідають елементам цієї множини. Якщо a_iRa_j і a_jRa_i, то вершини зв’язуються двома протилежно спрямованими дугами, які умовно можна замінювати однією не спрямованою дугою (ребром). Співвідношенню a_iAa_i відповідає петля.

а

б

в

Рис 2.2. Графи універсального (а), тотожного (б) та порожнього (в) відношень.

Нехай A={1,2,3,4}. Тоді граф універсального відношення на А зображено на рис. 2.2,а, граф тотожного відношення на А – на рис. 2.2,б, а граф порожнього відношення на А – на рис 2.2,в.

Матриця оберненого відношення R^-1 для відношення R – це транспонована матриця відношення R. Граф оберненого відношення R^-1 утворюється із графа відношення R заміною всіх дуг на протилежні.

Матриця композиції відношень T = R°S утворюється як добуток матриць відношень R та S з подальшою заміною відмінних від нуля елементів одиницями.

Справді, елемент t_ik матриці композиції знайдемо як суму добутків відповідних елементів матриць R та S (відповідно до правила множення матриць):

t_ik = r_i1s_1k + r_i2s_2k + … + r_ins_nk = .

Очевидно, така сума відмінна від нуля тоді й тільки тоді, коли хоча б один доданок відмінний від нуля, тобто дорівнює одиниці:

r_ijs_jk = 1 Û r_ij =1 та s_jk = 1 Û a_iRb_j та b_jSc_k Û a_iR°Sc_k.

Якщо у виразі t_ik не один, а кілька одиничних доданків, то кожен з них відповідає одному й тому самому співвідношенню a_iR°Sc_k, через що їх сума має бути замінена одиницею.

Для композиції відношень R = {(1,2), (2,1), (2,2), (3,3), (3,4)} та S={(1,1), (1,2), (2,3), (2,5), (3,2), (3,4), (4,2) (4,3)} матриця утворюється так:

Нехай RÍA´B та SÍB´C. Щоб побудувати граф T = R°S, потрібно до графа відношення R добудувати граф відношення S. Граф композиції відношень дістанемо, якщо вилучимо вершини, які відповідають елементам множини B. При вилученні вершини b_j кожний шлях, що проходить через неї від вершин множини А до вершин множини C, замінюється однією дугою з тим самим напрямком.

Для останнього прикладу маємо наступний граф:

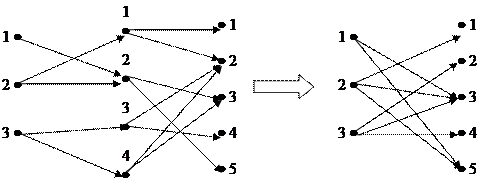
Рис 2.3. Граф композиції відношень.

Дата добавления: 2014-01-07