Еволвентне зачеплення

Тема 6.2.

Широке застосування знайшло евольвентне зачеплення, яке запропонував Л.Ейлер. В цьому зачепленні профіль зуба має форму евольвенти – особої кривої, яка є траєкторією руху точки, яка лежить на прямій, під час кочення цієї прямої по колу заданого діаметру без проковзування (рис.6.2).

Рис.6.2. Утворення евольвенти.

Колеса нарізаються зубчастою рейкою, однією рейкою можна нарізати колеса з різною кількістю зубців, при цьому правильність зачеплення не порушується при відхиленні міжосьової відстані від розрахункового значення. Допускаєьтся корегування (виправлення) робочого профілю з метою вибору оптимальних відрізків евольвенти.

Зубці з евольвентним профілем можуть бути нарізані на зубчастих колесах як зовнішнього, так і внутрішнього зачеплення.

На рис. 6.3. показане зачеплення зубців з евольвентним профілем двох зубчастих коліс. При перекочуванні прямої NN без ковзання по колу діаметром точка , що належить прямій NN, описує евольвенту, яка є профілем зубця колеса 1, а при перекочуванні прямої NN по колу діаметром точка описує евольвенту, яка є профілем зубця колеса 2. Пряма NN називається відтворюючою, а кола діаметром та називаються основними. Точка перетину спільної відтворюючої прямої NN iз лінією центрів зубчастих коліс називається полюсом зачеплення. Пряма NN є спільною нормаллю у точці до евольвент, що описують профілі зубців коліс 1 і 2, а відрізки АР і ВР є відповідними радіусами кривини профілів зубців у точці Р їхнього дотикання.

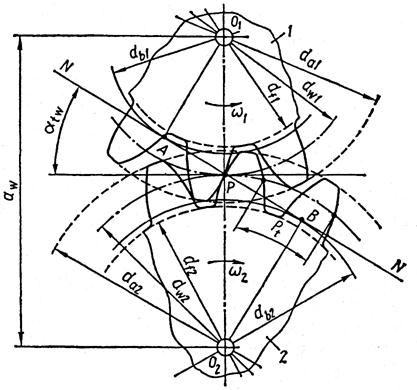
Рис. 6.3 Зубчасте зачеплення.

При обертанні зубчастих коліс точка дотикання профілів зубців постійно знаходиться на лінії NN, тобто спільна нормаль до профілів зубців займає постійне положення.

Основний закон зачеплення стверджує, що профілі зубців двох коліс повинні бути такими, щоб спільна нормаль до них у довільній точці дотикання профілів проходила через полюс зачеплення Р, який ділить міжосьову відстань O₁O₂ на відрізки, обернено пропорційні кутовим швидкостям зубчастих коліс.

Отже, евольвентне зачеплення відповідає вимогам основного закону зачеплення, оскільки точка Р займає постійне положення на лінії центрів O₁O₂. Відповідно з основним законом зачеплення

Рівність колових швидкостей зубчастих коліс 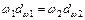свідчить про те, що при обертанні зубчастих коліс кола діаметрами та перекочуються одне по одному без ковзання. Ці кола називаються початковими колами, а відповідні їм циліндри у циліндричній і конуси у конічній зубчастих передачах називаються початковими циліндрами і початковими конусами. Діаметри та називаються початковими діаметрами зубчастих коліс.

Єдиним параметром, що визначає форму евольвенти, є діаметр основного кола , оскільки кожному конкретному колу відповідає одна певна евольвента. Зі збільшенням діаметра евольвента стає більш полога, а при перетворюється у пряму лінію. У цьому разі зубчасте колесо перетворюється у зубчасту рейку, яка має прямолінійний профіль зубців.

Із наведеного вище випливає, що відтворююча пряма (спільна нормаль NN) є лінією зачеплення, тобто геометричним місцем точок контакту спряжених зубців при обертанні зубчастих коліс.

Кут 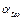між лінією зачеплення та прямою, перпендикулярною до міжосьової лінії, називається кутом зачеплення.

Співвісна циліндрична поверхня зубчастого колеса, яка є базою для визначення розмірів елементів зубців, називається ділильною поверхнею (ділить зубець на дві частини — головку та ніжку).

Концентричне коло, що лежить у торцевому перерізі колеса і належить ділильній поверхні, називається ділильним колом. Діаметри ділильних кіл позначають 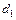i 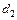називають ділильними діаметрами зубчастих коліс. На рис. 6.3. ділильні та початкові кола збігаються.

За висотою зубці обмежені поверхнею вершин зубців та поверхнею впадин зубців. Концентричне коло, що належить поверхні вершин, називається колом вершин, а концентричне коло, що належить поверхні впадин, називається колом впадин. Діаметри кіл вершин зубців позначаються i (відповідно для шестерні та колеса на рис. 6.3) і називаються діаметрами вершин зубців. Відповідно діаметри кіл впадин позначаються i і називаються діаметрами впадин.

Відстань між одноіменними профілями двох сусідніх зубців по дузі концентричного кола зубчастого колеса називається коловим кроком зубців і позначається 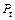(рис. 6.4. а). Розрізняють ділильний, початковий та інші колові кроки зубців, що відповідають ділильному, початковому та іншим концентричним колам зубчастого колеса. Для косих та криволінійних зубців крім колового кроку 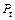(рис. 6.4. б, в), розрізняють нормальний крок зубців (рис. 6.4. б, в), який є найкоротшою відстанню по ділильному або однотипному співвісному колу зубчастого колеса між одноіменними профілями двох сусідніх зубців, а також осьовий крок зубців . (рис. 6.4 б)

а	б	в	г
Рис. 6.4 Форма та розміри зубців зубчастих коліс

Центральний кут концентричного кола зубчастого колеса, який дорівнює , де z — число зубців зубчастого колеса, називається кутовим кроком зубців і позначається .

Лінія перетину бічної поверхні зубця з ділильною, початковою або іншими співвісними поверхнями зубчастого колеса називається лінією зубця.

Гострий кут між лінією зубця та лінією перетину, співвісної поверхні, якій належить ця лінія зубця, з площиною, що проходить через вісь зубчастого колеса, називається кутом нахилу лінії зубця, або кутом нахилу зубця. Кут нахилу зубця позначається (рис. 6.4 б, в).

Кут повороту зубчастого колеса від моменту входу зубця в зачеплення до моменту виходу його із зачеплення називається кутом перекриття і позначається .

Відношення кутa перекриття зубчастого колеса передачі до його кутового кроку називається коефіцієнтом перекриття і позначається :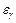

Коефіцієнт перекриття визначає середнє число пар зубців, що одночасно знаходяться у зачепленні. Якщо , то це означає, що 0,4 періоду зачеплення одного зубця у зачепленні знаходиться одна пара зубців, а 0,6 періоду зачеплення того самого зубця у зачепленні знаходяться дві пари зубців.

Із збільшенням коефіцієнта перекриття підвищуються плавність роботи та несуча здатність передачі, зменшуються динамічні навантаження та шум передачі. Тому у швидкохідних та високонавантажених передачах замість прямозубих використовують косозубі, шевронні колеса або колеса з криволінійними зубцями, які забезпечують більші коефіцієнти перекриття.

Коефіцієнт перекриття завжди повинен бути більшим за одиницю, у противному разі при роботі зубчастої передачі можуть виникнути моменти, коли у зачепленні не буде знаходитися жодна пара зубців і передача буде працювати з ударами.

Лінійна величина, що в раз менша за коловий крок зубців, називається коловим модулем зубців m_t, а лінійна величина, що в раз менша за нормальний крок зубців, називається нормальним модулем зубців m_n:

,

Для косих та криволінійних зубців

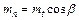
а для прямих зубців .

Модуль зубців є основною характеристикою розмірів вінців зубчастих коліс.Модулі зубців стандартизовані згідно ГОСТ 9563 — 60. Стандартні модулі від 1 до 18 мм такі:

1-й ряд: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16

2-й ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18

Ділильний діаметр косозубого колеса:

,

Для прямозубого зубчастого колеса відповідно маємо:

.

До параметрів евольвентного зачеплення належить також кут профілю зубця. Гострий кут у поперечному перерізі зубця між дотичною до профілю зубця у даній точці та лінією, яка проходить через цю точку і центр колеса, називається кутом профілю зубця (рис. 6.4. г). Розрізняють ділильний , початковий та інші кути профілю зубця, які відповідають точкам на ділильній, початковій та інших співвісних циліндричних поверхнях. У разі збігання початкових та ділильних коліс початковий кут профілю зубця дорівнює куту зачеплення .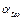

Ділильне коло – постійна геометрична фігура даного зубчастого колеса, діаметр якого залежить тільки від модуля та кількість зубців.

Початкове коло – поняття кінематичне і у окремо взятого колеса такого кола не має. Про початкові кола говорять, коли розглядають колеса, що знаходяться у зачепленні. Як зазначалось вище, ці кола стикаються у полюсі зачеплення і при обертанні зубчастих коліс перекочуються одне по другому без ковзання. Не можна змішувати поняття початкового та ділильного кіл зубчастих коліс.

Якщо міжосьова відстань зубчастої передачі:

,

то ділильні і початкові кола зубчастих коліс збігаються. При зміні міжосьової відстані передачі діаметри ділильних кіл не змінюються, а діаметри початкових кіл змінюються пропорційно зміні .Тоді

де і – передавальне число зубчастої передачі за співвідношенням. Його також визначають і як відношення чисел зубців зубчастого колеса

.

При безмежно великому діаметрі основного кола зубчасте колесо перетворюється у зубчасту рейку, а евольвентний профіль в прямолінійний.

рис. 6.5

Якщо число зубців 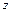менше від , то при нарізанні зубців рейкою відбувається підріз ніжки зуба. Для того щоб цього уникнути застосовують корегування зубчастих зачеплень (рис. 6.5). Також корегування дозволяє вписати зубчасте зачеплення (передачу) у наперед задану міжосьову відстань.

Кореговане зачеплення відрізняється від нормального тим, що профілі зубців виконують іншим, більш доцільним для даної передачі відрізками евольвенти того самого основного кола. Виготовляють кореговані передачі на тому ж самому обладнанні, що й не кореговані. Різниця полягає в тому, що для корегованих коліс інструмент встановлюють з деяким зміщенням у радіальному напрямі .

Зміщення початкового контуру:

де х – коефіцієнт зміщення, т – модуль зубців.

Коефіцієнт зміщення , якщо інструмент зміщують від центра заготовки і від’ємним , якщо інструмент зміщують до центра заготовки.

Лекція 11. Тема 6.3.

ТОЧНІСТЬ ЗУБЧАСТИХ ПЕРЕДАЧ

Основні показники точності:

Дата добавления: 2014-01-07