Ризик в абсолютному вираженні

Система кількісних оцінок економічного ризику.

Для здійснення кількісної оцінки економічного ризику підприємець повинен керуватись двома категоріями:

1). Величиною очікуваних втрат спричинених конкретним рішенням.

2). Ймовірністю настання цих втрат.

Для оцінювання ймовірності може застосовуватись один із двох методів:

1). Суб’єктивний метод оцінки ймовірності.

2). Об’єктивний метод (обробка статистичних даних).

Система кількісних оцінок ризику в абсолютному виразі складається з таких:

· У випадку, коли рішення є альтернативним, тобто можливі лише два наслідки його реалізації, показники ризику розраховуються за такою залежністю:

R = Xн * Рн, (9.1),

де Хн – величина збитків у разі настання негативного наслідку рішення, Рн – ймовірність настання негативного наслідку.

· У випадку, якщо рішення мають декілька (безліч) наслідків реалізації, використовують показники:

а) математичне сподівання. Математичне сподівання дискреційної величини представляє собою суму добутків можливих варіантів цієї величини на їх імовірність: М(х)= (9.2),

при чому основною умовою використання цієї формули є: (9.3).

Математичне сподівання для неперервної величини: М(х)=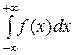 (9.4);

б) показник дисперсії характеризує ступінь мінливості реальних даних деякої випадкової величини навколо математичного сподівання. Визначається як математичне сподівання квадратів відхилень індивідуальних значень випадкової величини від її математичного сподівання: σ²=М(х – М(х))²

Для дисперсійної величини формула дисперсії має вигляд:

σ²= (9.5).

Для неперервної величини: σ²= (9.6).

в) середньо квадратичне відхилення:

σ = (9.7);

σ = (9.8).

Іноді для оцінки величини ризику в абсолютному виразі використовують ймовірність настання небажаних наслідків, тобто величини Р. Для неперервних величин при оцінці ризику іноді достатнім є зображення густоти розподілу випадкових величин Х на графіку (Рис. 9.5):

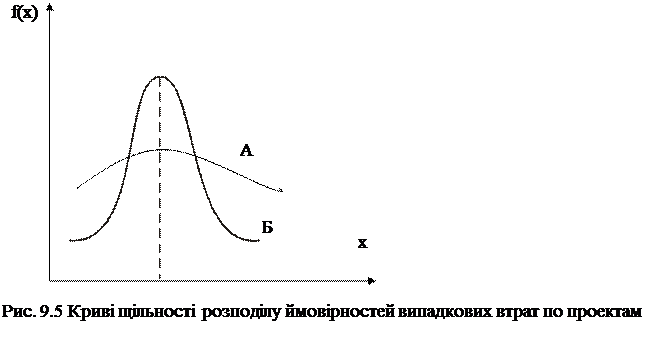З наведених на малюнку прикладів розподілу віддачі проекту А і Б можна зробити висновок, що ризик проекту Б є меншим ніж ризик проекту А, оскільки менша його розсіюваність навколо середнього значення.

2.2. Ризик у відносному виразі. Іноді для оцінки ризику при обґрунтуванні рішення не достатньо абсолютних показників. У такому випадку здійснюють розрахунок відносних показників. У відносному виразі ризик визначається:

1). коефіцієнтом ризику, який визначається як відношення величини максимальних втрат від даного виду діяльності до деякої бази порівнянь (за таку базу може прийматись обсяг власних ресурсів підприємства, загальні величини втрати по даному виду діяльності або сподіваний дохід від даного виду діяльності):

, (9.9)

де Х – величина максимально можливих втрат; К – база порівнянь.

Приклад: Емігрант з України включається в гру на фондовій біржі після того як отримав роботу і має стабільний дохід. Заощадивши власні 10000 доларів, він взяв у борг ще 40000 доларів під 10%-річних і вклав всі 50000 доларів в акції однієї з компаній, розраховуючи на річне зростання курсу 20%. Але фактичний курс почав падати з ряду причин і коли він знизився на 40% емігрант вирішив позбутися ненадійних акцій, у результаті чого збитки привели його до банкрутства. Його знайомий американець також вклав власні 50000 доларів в акції тієї ж фірми, а потім продав їх, проте американцю вдалося уникнути банкрутства. Чому збанкрутував емігрант?

Розв’язок:

1). Визначаємо збитки, які зазнав емігрант: 10000+40000·1,1-30000=24000 доларів.

Власний капітал емігранта 10000 доларів.

2). Збитки американця дорівнюють 20000 доларам: вклав 50000 дол., повернув 30000 дол. Власний капітал 50000 доларів.

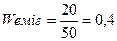
У наведеній фінансовій операції ступінь ризику емігранта у 6 разів переважав ступінь ризику американця, тому він і зазнав банкрутства.

2). Коефіцієнт варіації

σ_в= (9.10).

Цей показник, як правило завершує проведення дисперсійного аналізу ризику і використовується при наявності масиву статистичної інформації. При чому, чим більший цей показник, тим більшим є ризик, пов’язаний з даним проектом.

2.3. Ризик та нерівність Чебишева. Дисперсійний аналіз іноді не повністю характеризує ризик проекту. Проте дає необхідний матеріал для оцінки граничних шансів інвестора. Теоретичною базою для цього є нерівність Чебишева, яка має такий вигляд: ймовірність того, що випадкова величина відхиляється по модулю від свого математичного сподівання більше ніж на задану величину σ не перевищує дисперсії цієї величини поділеної на квадрат :

Р{ }≤ 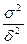(9.11).

При цьому необхідною умовою для виконання нерівності є:

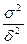≤ 1 або σ²≤ (9.12).

Приклад (застосування нерівності Чебишева для обґрунтування рішень):

Припустимо, що інвестиції здійснюються за рахунок кредиту взятого під відсотки r_s під заставу нерухомості. Яка ймовірність того, що інвестор не зможе повернути свій борг і позбудеться нерухомості.

Розв’язок: Інвестор позбудеться нерухомості, якщо реальна віддача буде меншою за відсотое по кредиту:

R < r_s (9.13)

-(R – m) > m – r_s (9.14)

Р{êR – m ê>m – r_s }≤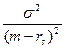 (9.15).

Виходячи з останньої формули, шанс збанкрутувати для підприємства не перевищує величину σ² / (m – r_s)².

Звичайно, при цьому обов’язковою є умова раціональності кредиту, коли m>r_s. Таким чином задаючись ймовірністю банкрутства, підприємець може визначити проекти, віддача яких знизить небезпеку банкрутства. Так, якщо прийняти ймовірність банкрутства 1/9, то достатньо щоб виконувалось правило “трьох σ”.

Якщо ймовірність 1/9, то 1/9 ³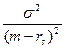 (9.16)

m ≥ r_s + 3σ (9.17)

Дата добавления: 2014-01-07