Основні теоретичні положення

Лекція №9. Лінії другого порядку на площині.

Опорні конспекти лекцій

І КУРС

Лисенко В.І.

«Вища математика»

Література:

1. Тевяшев А.Д.; Литвин О.Г.; Вища математика у прикладах та задачах; ч. I- к: Кондор, 2006 – 588с. (с.60-62)

2. Данко П.Е. Высшая математика в примерах и задачах ч I – М – 2005, 304 с (с.25- 38)

3. Дубовик В.П., Юрик І.І. вища математика: Навчальний посібник- К: А.С.К. 648 с.(с.98-112).

Кривими лініями другого порядку називають лінії, координати точок яких задовольняють рівняння кривої другого порядку.

Загальне рівняння кривої другого порядку

Ах²+2Вху+Су²+Дх+Еу+F=0, де

1.Коло. Колом називають множину всіх точок площини, відстані від яких до заданої точки (центра кола) дорівнюють сталому числу (радіусу).

Нехай у прямокутній системі координат на площині задані

О (а;в) – центр кола, М(х;у) – довільна точка та R – радіус кола. Точка М лежить на колі тоді і тільки тоді, коли ОМ=R.

Тобто 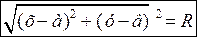(1)

Рівняння (1) є шуканим рівнянням кола. Піднесемо до квадрата обидві частини. Одержимо (х- а)²+(у- в)²=R² (2) – рівняння кола з центром (а;в)і радіусом R.

Якщо центром кола є початок координат, то а=в =0 і рівняння (2) набирає вигляду

х²+у²= R² (3) – канонічне рівняння кола.

Якщо у рівнянні (2) розкрити дужки, то одержимо

х²-2ах+а²+у²-2ву+в²= R² (4).

В загальному вигляді рівняння х²-2 а х+у²-2 в у=R²- а ²- в ² (5) визначає коло, якщо

R²-а²-в²>0, відсутній член з ху і коефіцієнти при х² та у² рівні між собою. При R²-а²-в²<0 рівняння не має геометричного образу.

Приклад 1. Знайти центр і радіус кола

х²+у²+4x-6у-23=0.

Розв’язання

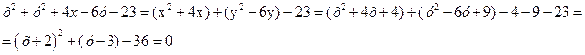
Звідки (х+2)²+(у-3)²=36.

О(-2;3), R=6.

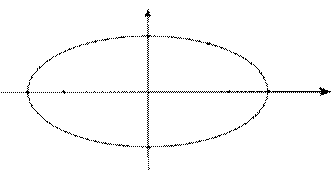
2.Еліпс. Еліпсом називають множину всіх точок площини, сума відстаней яких від двох даних точок цієї площини, які називаються фокусами, є величина стала і більша від відстані між фокусами.

Нехай F₁ і F₂ фокуси еліпса у прямокутній системі координат, Ох проходить через F₁ і F₂ початок координат ділить відрізок F₁F₂ навпіл.

a) б)

Рис.1

Нехай F₁F₂=2с, тоді F₁(-с;0), F₂(с;0). М(х;у)- довільна точка, яка належить еліпсу, а F₁М+ F₂М=2 а. Тобто (6)

Формула (6) задає еліпс.

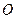Спростимо її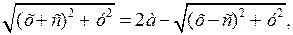

; звідки , ,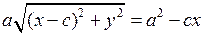

,

, .

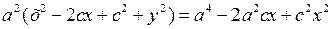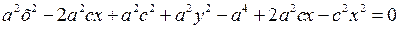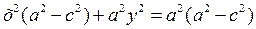Позначимо 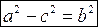(7) (бо a>c).

Одержимо: . Тоді

(8) - канонічне рівняння еліпса з центром О(0;0), велика та мала півосі відповідно дорівнюють а та b.

Примітка 1.

1. Рівняння еліпса містить тільки в парних степенях х та у, тому разом з точкою М(х;у) еліпсу належатимуть точки з координатами (-х;у),

(-х;-у), (х;-у). Значить еліпс симетричний відносно осей Ох, Оу та відносно початку координат. Він вміщується в прямокутник зі сторонами 2а та 2b.

2. Якщо а=b, то рівняння (8) набуває виду 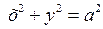. А це рівняння кола.

3. Міра відхилення еліпса від кола характеризується величиною, яка називається ексцентриситетом еліпса 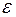і дорівнює відношенню половини фокальної відстані до довжини більшої півосі. 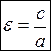(9) – ексцентриситет еліпса.

Причому 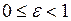, оскільки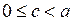

4. Нехай М(х;у) – довільна точка еліпса з фокусами F₁ та F₂. відстан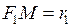і і 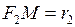– називають фокальними радіусами точки М. 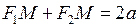за означенням еліпса. Прямі 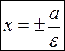(10) називаються директрисами еліпса.

Рис. 2

Відношення фокальних радіусів довільної точки М до відстаней цієї точки від відповідних директрис є величина стала і дорівнює ексцентрицитету. (11).

5. Якщо центром еліпса з півосями а і b є точка 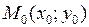, то його рівняння має вигляд 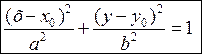(12)

Приклад 2. Скласти канонічне рівняння еліпса, фокуси якого лежать на осі Ох симетрично початку координат, якщо відстань між фокусами дорівнює 14, а ексцентриситет дорівнює .

Розв’язання

Канонічне рівняння еліпса має вигляд: 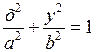, а ексцентрицитет 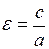, де . Тоді , .

З рівності (7): , .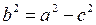

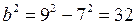Рівняння еліпса матиме вигляд: .

Приклад 3. Довести, що в полярній системі координат рівняння еліпса має вигляд: .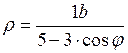

Розв’язання.

Оскільки , , 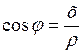то задане рівняння приймає вигляд ,

_,

5

25, ,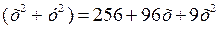

, ,

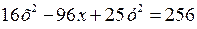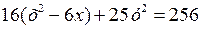
– еліпс з центром (3;0) і півосями а =5, b=4.

3. Гіпербола.

Гіперболою називають множину всіх точок площини, модуль різниці відстаней яких від двох точок і 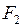(фокусів) є величиною сталою і дорівнює 2а.

Якщо вісь Ох проходить через фокуси і 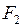, вісь Оу – через середину відрізка 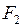, то канонічне рівняння гіперболи має вигляд:

(13)

Осі Ох і Оу – є осями симетрії, а точка О(0;0) є центром симетрії гіперболи. Точки та перетину гіперболи з віссю Ох є вершинами гіперболи, а точки і – її фокусами, причому (14). Число а – називають дійсною піввіссю, а число b –уявною піввіссю гіперболи. (13).

Щоб побудувати графік гіперболи, треба:

1) побудувати прямокутник зі сторонами 2а та 2b, точка перетину діагоналей якого співпадає з точкою О(0;0);

2) провести прямі 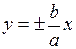, що містять діагоналі прямокутника –асимптоти гіперболи;

3) побудувати фокуси гіперболи;

4) побудувати вітки гіперболи, з вершинами в точках 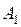та .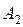

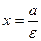
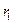
Рис. 3

Ексцентрицитет гіперболи (13) –це відношення відстані між фокусами до дійсної осі 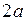, тобто 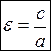, (15) причому .

Криву (16) – називають гіперболою спряженою до гіперболи (13). У цієї кривої дійсною піввіссю є число b, а уявною – число а, причому її фокуси лежать на осі Оу. У цьому випадку ексцентриситет гіперболи .

Якщо 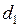і –відстані точки М(х;у) гіперболи від директрис, і –фокальні радіуси точки М, то .

Приклад 4.

Визначити канонічне рівняння гіперболи у якої уявна піввісь b=3, а ексцентриситет .

Розв’язання

Щоб записати канонічне рівняння гіперболи, треба знайти піввісь а.

Оскільки 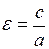, то 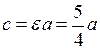. З рівності (12) одержимо 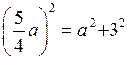, , , 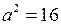звідки 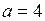. Отже, шукане рівняння гіперболи має вигляд .

Асимптотами даної гіперболи є прямі 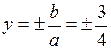, а директрисами –прямі .

Примітка. Якщо центром симетрії гіперболи є точка , то рівняння гіперболи має вигляд 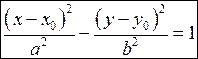(17).

Приклад 5.

Визначити вид і розміщення на площині даної кривої:

а) , б) ,

в) .

Розв’язання

а) – еліпс з центром в точці (1;-2) та півосями а =2; b=3.

б) – гіпербола з центром в точці (-2;4) та півосями а =4; b=3.

б) , , , 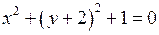– у множині дійсних чисел геометричного образу не існує (кажуть – порожня множина).

Дата добавления: 2014-01-07