Суперконвейерные процессоры

Ч

, Переход \

/ произошел \

i__________ ^^w Перехода _________ ^^^

/tr ^"^ч. ^не было j^"^ ^^v.

₁ г Предсказать, что Л------------------ ►• Предсказать, что N «

у^^ переход будет >/*~_п------------ Л^ перехода не будет )

^~~~~- -------- " произошел г^~ —"i^

\ Перехода ' \ не было.

Рис. 9.13. Диаграмма состояний автомата А1

Если команда завершилась переходом, то в соответствующий элемент РНТ за­носится единица, иначе — ноль. Очередное предсказание совпадает с итогом пре­дыдущего выполнения команды. После обработки очередной команды содержи­мое элемента корректируется.

Два других автомата предполагают большее число состояний, поэтому в них используются РНТ с многоразрядными элементами. Чаще всего ограничиваются двумя разрядами (т = 2) и, соответственно, автоматами с четырьмя состояниями.

В двухразрядном автомате А2 элементы РНТ отражают исходы двух последних выполненных команд условного перехода и заполняются по схеме регистра сдвига. После обработки очередной команды УП содержимое выделенного этой команде элемента РНТ сдвигается влево на один разряд, а в освободившуюся позицию за­носится единица (если переход был) или ноль (если перехода не было). Если в эле­менте РНТ присутствует хотя бы одна единица, то при очередном выполнении команды делается предсказание, что переход будет. При нулевом значении эле­мента РНТ считается, что перехода не будет. Диаграмма состояний для такого ав­томата показана на рис. 9.14.

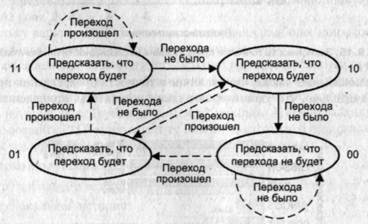
Рис. 9.14. Диаграмма состояний двухразрядного автомата А2

Двухразрядная схема автомата А2 используется относительно редко. Большую известность получила трехразрядная модель. Она, в частности, реализована в про­цессоре HP РА 8000.

Элементы РНТ в автомате A3 можно рассматривать как реверсивные счетчики, работающие в режиме с насыщением. При поступлении на конвейер команды ус­ловного перехода происходит обращение к соответствующему счетчику РНТ, и в зависимости от текущего состояния счетчика делается прогноз, определяющий дальнейший порядок извлечения команд программы. После прохождения ступе­ни исполнения, когда фактический исход команды становится ясным, содержи­мое счетчика увеличивается на единицу (если команда завершилась переходом) или уменьшается на единицу (если перехода не было). Счетчики работают в режи­ме насыщения. Это означает, что добавление единиц сверх максимального числа в счетчике, а также вычитание единиц при нулевом содержимом счетчика уже не

производятся. Основанием для предсказания служит состояние старшего разряд; счетчика. Если он содержит единицу, то принимается, что переход произойдет в противном случае предполагается, что перехода не будет.

Интуитивное представление о том, что с увеличением глубины предыстории (увеличением т) точность предсказания должна возрастать, на практике не под­тверждается. На рис. 9.15 показаны результаты одного из многочисленных иссле­дований, свидетельствующие, что при т > 3 точность предсказания начинает сни­жаться.

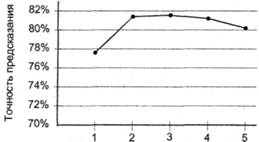
Разрядность счетчика в РНТ Рис. 9.15. Зависимость точности предсказания от разрядности элементов РНТ

График показывает также, что различие в точности предсказания при т = 3и m = 2 незначительно, что удостоверяют также результаты, приведенные в [197] (рис. 9.16).

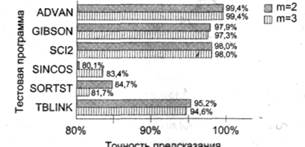
Рис. 9.16. Точность предсказания при использовании в РНТ двухразрядных и трехразрядных счетчиков

Как следствие, в большинстве известных процессоров используются двухраз­рядные счетчики (m = 2). Логика предсказания переходов применительно к двух­разрядным счетчикам известна как алгоритм Смита [193]. Алгоритм предполага­ет четыре состояния счетчика:

* 00 — перехода не будет (сильное предсказание);

■ 01 — перехода не будет (слабое предсказание);

■ 10 — переход будет (слабое предсказание);

11 — переход будет (сильное предсказание).

Рис. 9.17. Диаграмма состояний двухразрядного автомата A3

Логику предсказания можно описать диаграммой состояний двухразрядногс автомата A3 (рис. 9.17).

Поскольку вариант РНТ со счетчиками получил наиболее широкое распрост­ранение, в дальнейшем будем ссылаться именно на него.

После определения способов учета истории переходов и логики предсказания необходимо остановиться на особенностях использования таблицы, в частности на том, какая информация выступает в качестве шаблона для доступа к РНТ и ка­кого рода история фиксируется в элементах таблицы. Именно различия в спосо­бах использования РНТ определяют ту или иную стратегию предсказания.

В качестве шаблонов для доступа к РНТ могут быть взяты:

Ш адрес команды условного перехода;

Ш регистр глобальной истории;

■ регистр локальной истории;

Я комбинация предшествующих вариантов.

Схема, где для доступа к РНТ выбран адрес команды условного перехода (со­держимое счетчика команд), позволяет учитывать поведение каждой конкретной команды УП. При многократном выполнении большинства команд условного пе­рехода наблюдается повторяемость исхода: переход либо, как правило, происхо­дит, либо, как правило, не происходит (имеет место бимодальное распределение исходов). Индексация РНТ с помощью адреса команды УП дает возможность от­делить первые от вторых и, соответственно, повысить точность предсказания. Каж­дой команде условного перехода в РНТ соответствует свой счетчик. Когда коман­да завершается переходом, содержимое счетчика увеличивается на единицу, а в противном случае — уменьшается на единицу (естественно, с соблюдением логи­ки счета с насыщением). В качестве шаблона для поиска в РНТ служат младшие k разрядов содержимого счетчика команд (рис. 9.18).

При ^-разрядном индексе таблица может содержать 2 элементов.

Схема обеспечивает достаточно высокий процент правильных предсказаний для тех команд УП, которые в ходе вычислений выполняются многократно, например

Рис. 9.18. Индексирование РНТ с помощью адреса команды перехода

предназначены для управления циклом. В. то же время в любой программе имеет­ся достаточно много команд перехода, выполняемых лишь однократно или малое число раз. Как показали исследования, исход для таких команд в значительной мере зависит от поведения предшествующих им команд УП, связь которых с рас­сматриваемой командой не столь очевидна. Иными словами, между исходами ко­манд условного перехода в программе существует известная взаимосвязь, учет которой дает возможность повысить долю правильных предсказаний. Эта идея реализуется схемой с регистром глобальной истории.

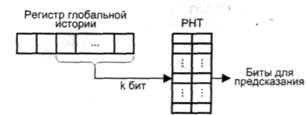
Регистр глобальной истории (GHR, Global History Register) представляет со­бой /-разрядный сдвиговый регистр (рис. 9.19). После выполнения очередной ко­манды условного перехода содержимое регистра сдвигается на один разряд, а в освободившуюся позицию заносится единица (если исходом команды был пере­ход) или ноль (если перехода не было). Следовательно, кодовая комбинация в GHR отражает историю выполнения последних / команд условного перехода. Под ин­дексирование массива предикторов (элементов механизма предсказания) выделя­ются k младших разряда GHR (чаще всего / = k). Каждой ^-разрядной комбинации исходов последовательно выполнявшихся команд УП в массиве дескрипторов со­ответствует свой счетчик. Таким образом, счетчик РНТ определяется тем, какая комбинация исходов имела место в k предшествовавших командах перехода. Со­держимое счетчика используется для предсказания исхода текущей команды пе­рехода и впоследствии модифицируется по результату фактического выполнения команды.

S

Рис. 9.19. Индексирование РНТ с помощью регистра глобальной истории

Регистр локальной истории (LHR, Local History Register) по логике работы ана­логичен регистру глобальной истории, но предназначен для фиксации последова­тельных исходов одной и той же команды УП. В схемах предсказания с LHR при­сутствует так называемая таблица локальной истории, представляющая собой массив регистров локальной истории (рис. 9.20).

Рис. 9.20. Индексирование РНТ с помощью регистров локальной истории

Как и в схеме с адресом команды перехода, каждый счетчик в РНТ фиксирует историю исхода только одной команды УП, но базируясь на более детальных зна­ниях, отражающих к тому же и последовательность исходов.

Ранее уже отмечалось, что действие команды условного перехода зависит не только от результатов предшествующих выполнений данной команды, но и от ис­хода других команд перехода. Учет обоих факторов позволяет повысить точность предсказаний. С этой целью в ряде динамических методов предсказания шаблон для доступа к РНТ формируется путем объединения адреса команды перехода и со­держимого GHR (либо LHR), при этом используется одна из двух операций: кон­катенация (сцепление) и сложение по модулю 2 («исключающее ИЛИ»).

При конкатенации ^-разрядный шаблон для обращения к РНТ образуется по­средством взятия q младших битов из одного источника, к которым пристыковы­ваются k-q младших разрядов, взятых из второго источника (рис. 9.21).

Регистр глобальной Счетчик команд

(локальной) истории

j ______ j рнт

У______________ - —---- — _^_ Биты для

--------- j^g^--------- *--------- ~г предсказания

Рис. 9.21. Формирование шаблона для доступа к РНТ путем конкатенации

Эффективность предсказания на основе подобного шаблона зависит от соотно­шения количества разрядов (q и k-q), выбранных от каждого из двух источников. Здесь многое определяется и характером программы. В качестве иллюстрации на рис. 9.22 приведена зависимость точности предсказания от соотношения числа битов, взятых от счетчика команд (СК) и регистра глобальной истории (GHR). Данные получены на тестовой программе xlisp (интерпретатор языка LISP) при объеме РНТ, равном 1024 входам.

Рис. 9.22. Зависимость точности предсказания от соотношения разрядов в шаблоне

при конкатенации [197J

Вариант со сложением по модулю 2 предполагает побитовое применение опе­рации «Исключающее ИЛИ» к обоим источникам (рис. 9.23). В качестве шаблона используются k младших разрядов результата. Сформированный шаблон содер­жит больше полезной информации для предсказания, чем каждый из источников по отдельности.

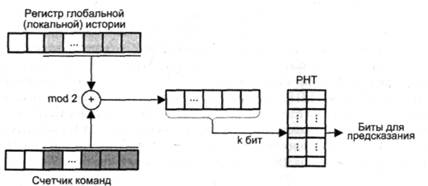
Рис. 9.23. Формирование шаблона для доступа к РНТ путем сложения по модулю 2

Для сравнительной оценки рассмотренных вариантов доступа к РНТ обратим­ся к результатам экспериментов, приведенным в [64]. Исследовались четыре тес­товых программы: в compress — сжатие файлов (10 млн УП);

■ eqntott — преобразование логических функций, заданных таблицей истиннос­ти (178 млн УП); espresso — минимизация логических функций (73 млн УП);

* xlisp — интерпретатор LISP (772 млн УП).

Результаты, усредненные по всем четырем программам для различных по объему таблиц РНТ, показаны на рис. 9.24.

Первый вывод, вытекающий из представленных данных, очевиден — с увели­чением размера РНТ точность предсказания возрастает. Среди четырех рассмот­ренных схем наилучшую точность обеспечивает схема со сложением по модулю два. Схема со счетчиком команд относится к наименее эффективным. Объясняет­ся это тем, что каждый отдельный счетчик РНТ в схеме со счетчиком команд за-действуется значительно реже, а некоторые счетчики вообще остаются без внима-

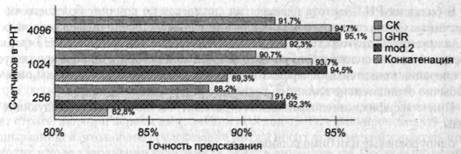
Рис. 9.24. Зависимость точности предсказания от способа доступа к РНТ и размера таблицы

ния. Результаты для схемы с конкатенацией получены для случая, когда в шабло­не используется одинаковое число разрядов из СК и GHR. При малых объемах РНТ вариант с конкатенацией дает наихудшие результаты, но при больших РНТ эта схема превосходит модель со счетчиком команд.

В реальных схемах предсказания переходов размер таблицы РНТ ограничен. Типичное количество элементов РНТ (элементарных счетчиков) в разных про­цессорах варьируется от 256 до 4096. Для выбора определенного входа в РНТ (нуж­ного счетчика) применяется ^-разрядный шаблон, где k определяется размером массива. Для упомянутых выше размеров РНТ значение k лежит в диапазоне от 8 до 12. Если обращение к РНТ определяется счетчиком команд, разрядность кото­рого обычно больше, чем k, в качестве шаблона выступают k младших битов СК. Как следствие, две команды условного перехода, адреса которых в младших k раз­рядах совпадают, будут обращаться к одному и тому же элементу РНТ, и история выполнения одной команды будет накладываться на историю выполнения дру­гой, что, естественно, будет влиять на точность предсказания. Ситуация известна как эффект наложения (aliasing). Та же проблема существует и при доступе к РНТ на основании содержимого регистра глобальной истории или регистра локальной исто­рии. В зависимости от типа программы и других факторов наложение может при­водить к повышению точности предсказания, ее ухудшению либо вообще не сказы­ваться на точности предсказания. Соответственно, эффекты наложения класси­фицируют как конструктивный, деструктивный и нейтральный.

Рассмотрим, насколько часто предсказания производятся на основании тех счетчиков РНТ, при обращении к которым имел место эффект наложения (рис. 9.25) [64].

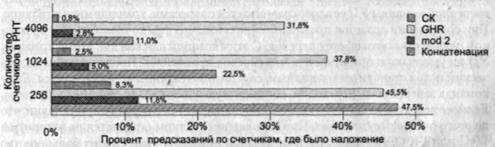
Рис. 9.25. Интенсивность наложения при различных способах доступа к РНТ

В больших РНТ частота перекрытия снижается по причине большего числа счетчиков. Схема со счетчиком команд в наименьшей степени подвержена эффек­ту наложения. С другой стороны, в схемах, где шаблон для доступа к РНТ форми­руется на основе содержимого регистра глобальной истории, причем использует­ся операция конкатенации, эффект наложения сказывается в значительной мере и обычно отрицательно влияет на точность предсказания переходов.

При классификации динамических стратегий обычно выделяют следующие их виды:

Ш одноуровневые или бимодальные; Я двухуровневые или коррелированные;

■ гибридные;

■ асимметричные.

Одноуровневые схемы предсказания переходов. В многочисленных исследо­ваниях, проводившихся на самых разнообразных программах, была отмечена ин­тересная закономерность. В поведении многих команд условного перехода явно прослеживается тенденция повторяемости исхода: одни команды программы, как правило, завершаются переходом, в то время как другие — остаются без оного, то есть имеет место бимодальное распределение исходов. Идея одноуровневых схем предсказания, известных также под вторым названием — бимодальные схемы [ 165], сводится к отделению команд, имеющих склонность завершаться переходом, от команд, при выполнении которых переход обычно не происходит. Такая диффе­ренциация позволяет для каждой команды выбрать наиболее подходящее пред­сказание. Для реализации идеи в составе схемы предсказания достаточно иметь лишь одну таблицу, каждый элемент которой отображает историю исходов одной команды УП. Для обращения к элементу, ассоциированному с определенной ко­мандой УП, используется адрес этой команды (или его младшие биты). Таким об­разом, одноуровневые схемы предсказания переходов можно определить как схе­мы, содержащие один уровень таблиц истории переходов (обычно единственную таблицу), адресуемых с помощью адреса команды условного перехода.

В первом из возможных вариантов одноуровневых схем строится сравнитель­но небольшая таблица, куда заносятся адреса п последних команд У П, при выпол­нении которых переход не случился. В сущности, это ранее упоминавшийся буфер адресов перехода (ВТВ), но с противоположным правилом занесения информа­ции (фиксируются адреса команд, завершившихся без перехода). Таблица обычно реализуется на базе ассоциативной кэш-памяти. При поступлении на конвейер очередной команды УП ее адрес сравнивается с адресами, хранящимися в таблице. При совпадении делается предположение о том, что перехода не будет, в против­ном случае предсказывается переход. С этих позиций для каждой новой команды УП по умолчанию принимается, что переход произойдет. После того как факти­ческий исход становится очевидным, содержимое таблицы корректируется. Если команда завершилась переходом, соответствующая запись из таблицы удаляется. Если же перехода не было, то адрес команды заносится в таблицу при условии, что до этого он там отсутствовал. При заполнении таблицы опираются на алгоритмы LRU или FIFO. По точности предсказания стратегия превосходит большинство стратегий статического предсказания.

Вторая схема ориентирована на то, что команды программы извлекаются из кэш-памяти команд. Каждая ячейка кэш-памяти содержит дополнительный раз­ряд, который используется только применительно к командам условного перехода. Состояние разряда отражает исход предыдущего выполнения команды (1 — пере­ход был, 0 — перехода не было). Новое предсказание совпадает с результатом пред­шествующего выполнения данной команды. При занесении такой команды в кэш-память рассматриваемый разряд устанавливается в единицу. Это напоми­нает стратегию «при первом выполнении переход обязательно происходит» с той лишь разницей, что первое предсказание, хотя и носит статический характер, про­исходит в ходе заполнения кэш-памяти, то есть динамически. После выполнения команды состояние дополнительного бита корректируется: если переход имел ме­сто, в него заносится единица, а в противном случае — ноль. Эффективность стра­тегии характеризуют данные, полученные в [197] (рис. 9.26).

Рис. 9.26. Точность предсказания схемы с дополнительным битом в кэш-памяти команд

Главный ее недостаток заключается в дополнительных затратах времени на обновление состояния контрольного разряда в кэш-памяти команд.

В третьей схеме (рис. 9.27) РНТ состоит из одноразрядных элементов и носит название таблицы истории переходов (ВНТ, Branch History Table).

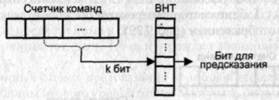
Рис. 9.27. Однобитовая бимодальная схема предсказания

Состояние элемента ВНТ определяет, произошел ли переход в ходе последнего выполнения команды условного перехода (1) или нет (0). Каждой команде УП в ВНТ соответствует свой элемент, для обращения к которому используются k младших разрядов адреса команды. Предсказание совпадает с исходом предыду­щего выполнения команды. Если команда условного перехода участвует в органи­зации цикла, то стратегия всегда приводит к неправильному предсказанию пере­хода в первой и последней итерациях цикла.

Схема была реализована в процессорах Alpha 21064 и AMD K5. Согласно результатам большинства исследований, средняя точность успешного прогно­за с помощью однобитовой бимодальной схемы не превышает 78%. В то же время в работе [197] получено значение 90,4%.

Точность предсказания перехода существенно повышается с увеличением разрядности элементов ВНТ. В четвертой из рассматриваемых одноуровневых схем каждый элемент ВНТ состоит из двух битов, выполняющих функцию двухразрядного счетчика, работающего в режиме с насыщением. Иными словами, реализуется алгоритм Смита. Каждый счетчик отображает историю выполнения одной команды УП, то есть адресуется младшими разрядами счетчика команд (рис. 9.28).

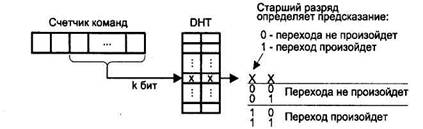
Рис. 9.28. Одноуровневая схема предсказания с таблицей DHT

Для обозначения таблицы истории переходов в данной схеме используют аббревиатуру DHT (Decode History Table). Слово «decode» (декодирование) в названии отражает особенность работы с таблицей. Если к обычной ВНТ обращение происходит при выборке любой команды, вне зависимости от того, на самом ли деле она команда условного перехода, поиск в DHT начинается только после декодирования команды, то есть когда выяснилось, что данная команда является командой условного перехода. Реализуется DHT на базе обычного ЗУ с произвольным доступом.

Последняя из обсуждаемых одноуровневых схем предсказания известна как схема Смита или бимодальный предиктор. Отличие от предыдущего варианта выражается лишь в способе реализации ВНТ (в схеме Смита сохранено именно это название таблицы). Таблица истории переходов организуется на базе кэш-памяти с ассоциативным отображением (рис. 9.29).

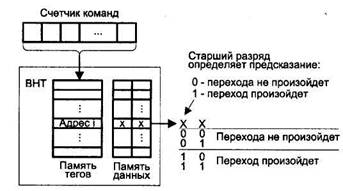
Рис. 9.29. Схема с таблицей истории переходов

В качестве ассоциативного признака (тега) при поиске нужного счетчика выступает адрес команды условного перехода. Такой подход позволяет ускорить поиск нужного счетчика и устраняет эффект наложения, но связан со значительными аппаратными затратами.

Результаты моделирования бимодальной схемы с двухразрядными счетчиками показаны на рис. 9.30. По этим данным среднюю точность предсказания можно оценить как 92,6%.

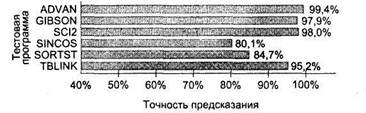
Рис. 9.30. Точность предсказания двухразрядной бимодальной схемы [197]

В экспериментах, где данная идея проверялась на программах тестового пакета SPEC_95, средняя точность предсказания по всем программам пакета составила 53,9%. Несмотря на это, бимодальная схема с двухразрядными счетчиками довольно распространена. На ее основе построены схемы предсказания переходов в процессорах Alpha 21164, R10000, PowerPC 620, UltraSPARC и др.

В заключение отметим, что во многих одноуровневых решениях таблица истории переходов (DHT или ВНТ) совмещена с буфером адреса перехода (ВТВ), что позволяет сэкономить на вычислении исполнительных адресов точек перехода.

Двухуровневые схемы предсказания переходов. Одноуровневые схемы предсказания ориентированы на те команды УП, очередной исход которых существенно зависит от их собственных предыдущих исходов. В то же время для многих команд программы наблюдается сильная зависимость не от собственных исходов, а от результатов выполнения других предшествующих им команд УП. Это обстоятельство призваны учесть двухуровневые адаптивные схемы предсказания переходов, впервые предложенные в [229]. Такие схемы часто называют коррелированными, подчеркивая тот факт, что они отражают взаимозависимость команд условного перехода.

В коррелированных схемах предсказания переходов выделяются два уровня таблиц. В роли таблицы первого уровня может выступать регистр глобальной истории (GHR), и тогда двухуровневую схему предсказания называют глобальной. В качестве таблицы первого уровня может также быть взят массив регистров локальной истории (LHR), где отдельный регистр отражает последовательность последних исходов одной команды УП. Такая схема предсказания носит название локальной. Каждый элемент таблицы второго уровня служит для хранения истории переходов отдельной команды УП. Таблица второго уровня обычно состоит из двухразрядных счетчиков и организована в виде матрицы (рис. 9.31). Содержимое счетчика команд (адрес команды УП) определяет один из регистров в таблице первого и одну строку в таблице второго уровня. В свою очередь, кодовая комбинация (шаблон), хранящаяся в выбранном регистре таблицы первого уровня, определяет нужный счетчик в указанном ряду таблицы второго уровня. Выбранный счетчик используется для формирования предсказания. После выполнения команды содержимое регистра и счетчика обновляется.

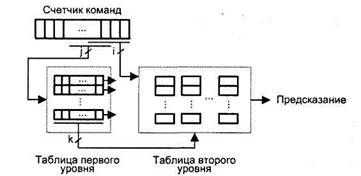
Рис. 9.31. Общая структура двухуровневой схемы предсказания переходов

Из описания логики двухуровневого предсказания следует, что выбор нужного счетчика обусловливается двумя источниками — адресом команды, для которой делается предсказание, и шаблоном, отражающим историю предшествующих переходов. Того же эффекта можно добиться при помощи схемы двухразрядного бимодального предиктора, если для доступа к ВНТ использовать шаблон, сформированный путем сложения по модулю 2, как это показано на рис. 9.23. Такая схема известна под названием gshare.

Гибридные схемы предсказания переходов. Для всех ранее рассмотренных стратегий характерна сильная зависимость точности предсказания от особенностей программ, в рамках которых эти стратегии реализуются. Та же самая схема, прекрасно проявляя себя с одними программными продуктами, с другими может давать совершенно неудовлетворительные результаты. Кроме того, необходимо учитывать еще один фактор. Прежде уже отмечалось, что точность предсказания повышается с увеличением глубины предыстории переходов, но происходит это лишь после накопления соответствующей информации, на что требуется определенное время. Период накопления предыстории принято называть временем «разогрева». Пока идет «разогрев», точность предсказания весьма низка. Иными словами, ни одна из элементарных стратегий предсказания переходов не является универсальной — со всех сторон лучшей в любых ситуациях. Гибридные или соревновательные схемы объединяют в себе несколько различных механизмов предсказания — элементарных предикторов. Идея состоит в том, чтобы в каждой конкретной ситуации задействовать тот элементарный предиктор, от которого в данном случае можно ожидать наибольшей точности предсказания.

Гибридная схема предсказания переходов, предложенная Макфарлингом [165], содержит два элементарных предиктора, отличающихся по своим характеристикам (размером таблиц предыстории и временем «разогрева») и работающих независимо друг от друга. Выбор предиктора, наиболее подходящего в данной ситуации, обеспечивается селектором, представляющим собой таблицу двухразрядных счетчиков, которые часто называют счетчиками выбора предиктора (рис. 9.32).

Адресация конкретного счетчика в таблице (индексирование) осуществляется k младшими разрядами адреса команды условного перехода, для которой осуществляется предсказание. Обновление таблиц истории в каждом из предикторов производится обычным образом, как это происходит при их автономном использовании. В свою очередь, изменение состояния счетчиков селектора выполняется по следующим правилам. Если оба предиктора одновременно дали одинаковое предсказание (верное или неверное), содержимое счетчика не изменяется. При правильном предсказании от первого предиктора и неверном от второго содержимое счетчика увеличивается, а в противоположном случае — уменьшается на единицу. Выбор предиктора, на основании которого делается результирующая оценка, реализуется с помощью мультиплексора, управляемого старшим разрядом соответствующего счетчика селектора.

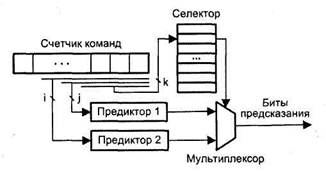
Рис. 9.32. Гибридный предиктор Макфарлинга

В работе [95] идея гибридного механизма была обобщена на случай n предикторов. Общая структура такой схемы предсказания переходов показана на рис. 9.33. При выполнении команды УП предсказания формируются одновременно всеми предикторами, однако реальные действия осуществляются на основании только одного из них.

Рис. 9.33. Общая схема гибридного предиктора

Выбор подходящего предиктора обеспечивает механизм селекции (рис. 9.34). В схеме имеется буфер предыстории переходов (ВТВ), в котором каждая запись дополнена п двухразрядными счетчиками выбора предиктора, по числу используемых элементарных предикторов. Счетчики позволяют отследить самый предпочтительный элементарный предиктор для каждой команды УП, представленной в ВТВ.

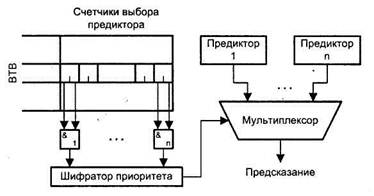
Рис. 9.34. Механизм выбора предиктора

При записи в ВТВ нового элемента во все ассоциированные с ним счетчики заносится число 3. Для каждой команды условного перехода предсказание генерируется всеми n предикторами, но во внимание принимаются только те из них, для которых соответствующий счетчик выбора предиктора содержит число 3. Если это число встретилось более чем в одном счетчике, выбор единственного предиктора, на основании которого и делается окончательное предсказание, обеспечивает шифратор приоритета. После выполнения команды условного перехода содержимое соответствующих ей счетчиков выбора обновляется, при этом действует следующий алгоритм. Если среди предикторов, счетчики которых равнялись 3, хотя бы один дал верное предсказание, то содержимое всех счетчиков, связанных с неверно сработавшими предикторами, уменьшается на единицу. В противном случае содержимое всех счетчиков, связанных с предикторами, прогноз которых подтвердился, увеличивается на единицу. Такая политика гарантирует, что по крайней мере в одном из счетчиков будет число 3. Еще одно преимущество рассматриваемой схемы выбора состоит в том, что она позволяет, например, отличить предиктор-«оракул», давший правильное предсказание последние пять раз, от предиктора, верно определившего исход последние четыре раза. Стандартные счетчики с насыщением такую дифференциацию не обеспечивают.

По имеющимся оценкам, точность предсказания переходов с помощью гибридных стратегий в среднем составляет 97,13%, что существенно выше по сравнению с прочими вариантами.

Асимметричная схема предсказания переходов. Асимметричная схема сочетает в себе черты гибридных и коррелированных схем предсказания. От гибридных схем она переняла одновременное срабатывание нескольких различных элементарных предикторов. В асимметричной схеме таких предикторов три, и каждый из них использует собственную таблицу РНТ. Для доступа к таблицам, аналогично коррелированным схемам, используется как адрес команды условного перехода, так и содержимое регистра глобальной истории (рис. 9.35).

Шаблон для обращения к каждой из трех РНТ формируется по-разному (применены различные функции хэширования). При выполнении команды условного перехода каждый из трех предикторов выдвигает свое предположение, но окончательное решение принимается по мажоритарной схеме. После завершения команды условного перехода содержимое всех трех таблиц обновляется.

Рис. 9.35. Структура асимметричной схемы предсказания переходов

Правильный подбор алгоритмов хэширования позволяет практически исключить влияние на точность предсказания эффекта наложения. Средняя точность предсказания с помощью асимметричной схемы, полученная на тестовом пакете SPEC_95, составила 72,6%.

Эффективность конвейера находится в прямой зависимости от того, с какой частотой на его вход подаются объекты обработки. Добиться n -кратного увеличения темпа работы конвейера можно двумя путями:

ü разбиением каждой ступени конвейера на n «подступеней» при одновременном повышении тактовой частоты внутри конвейера также в n раз;

ü включением в состав процессора n конвейеров, работающих с перекрытием.

В данном разделе рассматривается первый из этих подходов, известный как суперконвейеризация (термин впервые был применен в 1988 году). Иллюстрацией эффекта суперконвейеризации может служить диаграмма, приведенная на рис. 9.36, где рассмотрен ранее обсуждавшийся пример (см. рис. 9.3). Каждая из шести ступеней стандартного конвейера разбита на две более простые подступени, обозначенные индексами 1 и 2. Выполнение операции в подступенях занимает половину тактового периода. Тактирование операций внутри конвейера производится с частотой, вдвое превышающей частоту «внешнего» тактирования конвейера, благодаря чему на каждой ступени конвейера можно в пределах одного «внешнего» тактового периода выполнить две команды.

В сущности, суперконвейеризация сводится к увеличению количества ступеней конвейера как за счет добавления новых ступеней, так и путем дробления имеющихся ступеней на несколько простых подступеней. Главное требование — возможность реализации операции в каждой подступени наиболее простыми техническими средствами, а значит, с минимальными затратами времени. Вторым, не менее важным, условием является одинаковость задержки во всех подступенях.

Критерием для причисления процессора к суперконвейерным служит число ступеней в конвейере команд. К суперконвейерным относят процессоры, где таких ступеней больше шести. Первым серийным суперконвейерным процессором считается MIPS R4000, конвейер команд которого включает в себя восемь ступеней. Суперконвейеризация здесь стала следствием разбиения этапов выборки команды и выборки операнда, а также введения в конвейер дополнительного этапа проверки тега, появление которой обусловлено архитектурой системы команд машины.

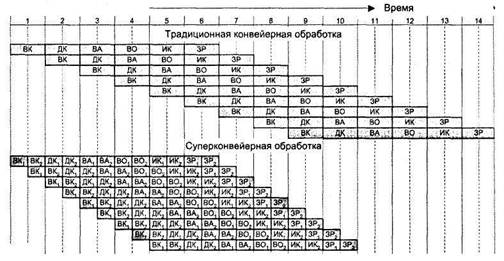
Рис. 9.36. Традиционная и суперконвейерная обработка команд

Таблица 9.1. Длина конвейера команд в популярных микропроцессорах

Тип микропроцессора	Количество ступеней в конвейере команд
MIPS R4400
UltraSPARC
Pentium III
Itanium
UltraSPARC III
Pentium 4

К сожалению, выигрыш, достигаемый за счет суперконвейеризации, на практике может оказаться лишь умозрительным. Удлинение конвейера ведет не только к усугублению проблем, характерных для любого конвейера, но и возникновению дополнительных сложностей. В длинном конвейере возрастает вероятность конфликтов. Дороже встает ошибка предсказания перехода — приходится очищать большее число ступеней конвейера, на что требуется больше времени. Усложняется логика взаимодействия ступеней конвейера. Тем не менее создателям ВМ удается успешно справляться с большинством из перечисленных проблем, свидетельством чего служит неуклонное возрастание числа ступеней в конвейерах команд современных процессоров (табл. 9.1).

Архитектуры с полным и сокращенным набором команд

Современная технология программирования ориентирована на языки высокого уровня (ЯВУ), главная задача которых — облегчить процесс написания программ. Более 90% всего процесса программирования осуществляют на ЯВУ. К сожалению, операции, характерные для ЯВУ, отличаются от операций, реализуемых машинными командами. Эта проблема получила название семантического разрыва и ведет она к недостаточно эффективному выполнению программ. Пытаясь преодолеть семантический разрыв, разработчики ВМ расширяют систему команд, дополняя ее командами, реализующими сложные операторы ЯВУ на аппаратурном уровне, вводят дополнительные виды адресации и т. п. Вычислительные машины, где реализованы эти средства, принято называть ВМ с полным набором команд (CISC — Complex Instruction Set Computer). К типу CISC можно отнести практически все ВМ, выпускавшиеся до середины 80-х годов и значительную часть из выпускаемых в настоящее время.

Характерные для CISC способы решения проблемы семантического разрыва, вместе с тем ведут к усложнению архитектуры ВМ, главным образом устройства управления, что, в свою очередь, негативно сказывается на производительности в целом. Кроме того, в CISC очень сложно организовать эффективный конвейер команд, который, как уже отмечалось, является одним из наиболее перспективных путей повышения производительности ВМ. Все это заставило более внимательно проанализировать программы, получаемые после компиляции с ЯВУ. Был предпринят комплекс исследований [128,158,177,178,209], в результате которых обнаружились интересные закономерности:

ü Реализация сложных команд, эквивалентных операторам ЯВУ, требует увеличения емкости управляющей памяти в микропрограммном УУ. Микропрограммы сложных команд могут занимать до 60% управляющей памяти, в то времякак их доля в общем объеме программы зачастую не превышает 0,2%.

ü В откомпилированной программе операторы ЯВУ реализуются в виде проце­дур (подпрограмм), поэтому на операции вызова процедуры и возврата из нее приходится от 15 до 45% вычислительной нагрузки.

ü При вызове процедуры вызывающая программа передает этой процедуре некоторое количество аргументов. Согласно [209], в 98% случаев число передаваемых аргументов не превышает шести. Примерно такое же положение сложилось и с параметрами, которые процедура возвращает вызывающей программе. Более 80% переменных, используемых программой [177,178], являются локальными, то есть создаются при входе в процедуру и уничтожаются при выходе из нее. Количество локальных переменных, создаваемых отдельной процедурой, в 92% случаев не превышает шести [209].

ü Почти половину операций в ходе вычислений составляет операция присваивания, сводящаяся к пересылке данных между регистрами, ячейками памяти или регистрами и памятью.

Детальный анализ результатов исследований привел к серьезному пересмотру традиционных архитектурных решений, следствием чего стало появление архитектуры с сокращенным набором команд (RISC — Reduced Instruction Set Computer). Термин «RISC» впервые был использован Паттерсоном и Дитцелем в 1980 году.

Дата добавления: 2014-01-07