
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розробка програми
|
|
|
|
2.1 Обчислювальна схема методу Рунге-Кута:
1. Виклик функції Yravnen() - приклади рівнянь користувачу.
2. Вводимо вихідні дані:
o а). номер рівняння, яке потрібно вирішити - chose;
o б). початок і кінець даного відрізка [x0,x];
o в). кількість кроків n;
o г). значення y0.
3. Обчислюємо величину кроку. h=(x-x0)/h
4. Привласнюємо у0 до першого елементу масиву у. y[0]=y0
5. Обчислюємо розв’язання рівняння, яке вибрали. Для цього робимо цикл від 0 до n і для кожного значення х обчислюємо значення у: for(int i=0; i<=n; i++)
{
· а). обчислюємо i-ий крок. x1=x0+i*h;
· б). визначаєм перший коефіциєнт даного методу. k1=h*F(x1,y[i],chose)
· в). визначаєм другий коефіцієнт даного методу. k2=h*F(x1+h/2,y[i]+k1/2,chose)
· г). визначаєм третій коефіцієнт даного методу. k2=h*F(x1+h/2,y[i]+k2/2,chose)
· д). визначаєм четвертий коефіцієнт даного методу.k2=h*F(x1+h,y[i]+k3,chose)
· е). обчислюємо значення у: y[i+1]=y[i]+(k1+2*k2+2*k3+k4)/6;
ж). виводимо значення у[i+1] при його значенні х1:cout <<x1<<” ”<<y[i+1]
}// кінець цикла при i=n.
6. Кінець програми.
Опис функції F(x,y, chose).
Функція має три формальні змінні:
· 1. значення х;
· 2. значення у;
· 3. номер обраного рівняння chose.
double F(float x,float y,int chose)
Дана функція, вибирає потрібне рівняння, по значенню chose:
double f;
if (chose==1) f=x+y;
if (chose==2) f=cos(x)+sin(y);
if (chose==3) f=2*x*x+sqrt(y+x);
if (chose==4) f=cos(x)+y/6;
if (chose==5) f=(x*x+2*y)/sin(x);
Дана функція повертає значення типу double
return f;
Опис функції Yravnen();
Дана функція не має формальних перемінних і повертає тип void.
У ній виводяться на екран приклади рівнянь для користувача:
cout<<"1. f=x+y \n";
cout<<"2. f=cos(x)+sin(y) \n";
cout<<"3. f=2*x*x+sqrt(y) \n";
cout<<"4. f=cos(x)+y/6 \n";
cout<<"5. f=(x*x+2*y)/sin(x) \n";
Блок – схема.




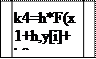

 |  | ||

 |
|
x, x0 , y0, ---------| (k1+2*k2+2*k3+k4)/6
n,chose |
 | |||
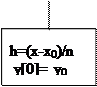 | |||

х1, y[i+1]

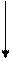 Yravnen()
Yravnen()



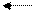 |  |

 1. f=x+y
1. f=x+y
2. f=cos(x)
 +sin(y)
+sin(y)
 |


3. f=2*x*x
 +sqrt(y)
+sqrt(y)
 |

 4.f=cos(x)
4.f=cos(x)
 + y/6
+ y/6
 |
 |

5.f=(x*x+

 2*y)/sin(x)
2*y)/sin(x)
 | |||
 | |||


 |  |
F(x,y)-вибір функції
 | |||
 |



 ні ні
ні ні
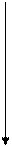 |  |

 так так
так так
 | 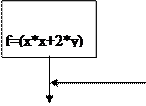 |

 ні
ні
 | |||
 |
 так
так
 |
ні
 | |||
 |

 так
так
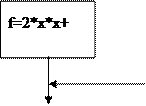 |
 ні
ні
 | |||
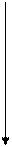 |
 так
так
 |
 | |||
 | |||


 |  |


x, x0 , y0,
n,chose
 |

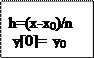 | |||||
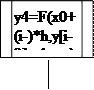 | |||||
 | |||||

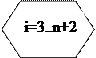 |
|


 -------------|(h/24)*(55*y1-59*y2+37*y3-*y4).
-------------|(h/24)*(55*y1-59*y2+37*y3-*y4).

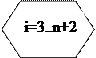 |
|



y[i+1]


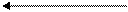 | |||
 |

 |
2.2 Обчислювальна схема методу Адамса:
1. Виклик функції Yravnen() - приклади рівнянь користувачу.
2. Вводимо вихідні дані:
а). номер рівняння, яке потрібно вирішити - chose;
б). початок і кінець даного відрізка [x0,x];
в). кількість кроків n;
г). значення y0.
3. Обчислюємо величину кроку. h=(x-x0)/h
4. Привласнюємо у0 до першого елемента масиву у. y[0]=y0
5. Обчислюємо розв’язання рівняння, яке вибрали. Для цього робимо цикл від 3 до n+2 і при кожнім наступному кроці обчислюємо значення у: for (int i=3; i<=n+2; i++)
{
а). обчислюємо i-ий шаг. x1=x0+(i-2)*h;
б). визначаємо перше початкове значення методу Адамса. y1=F(x0+i*h,y[i],chose)
в). визначаємо друге початкове значення методу Адамса. y2=F(x0+(i-1)*h,y[i-1],chose)
г). визначаємо третє початкове значення методу Адамса. y3=F(x0+(i-2)*h,y[i-2],chose)
д). визначаємо четверте початкове значення методу Адамса. y4=F(x0+(i-3)*h,y[i-3],chose)
е). обчислюємо значення у: y[i+1]=y[i]+(h/24)*(55*y1-59*y2+37*y3-9*y4);
ж). виводимо значення у[i+1] при його значенні х1: cout <<x1<<” ”<<y[i+1]
}// кінець цикла при i=n+2.
6. Кінець програми.
Функція F(x,y) має три формальні змінні і вона ідентична функції, що описана в методі Рунге-Кута.
Функція Yravnen() не має формальних перемінних, повертає значення типу void; описана вище, у методі Рунге-Кута.
2.3 Обчислювальна схема методу Крилова:
1. Виклик функції Yravnen() - приклади рівнянь користувачу.
2. Вводимо вихідні дані:
а). номер рівняння, яке потрібно вирішити - chose;
б). початок і кінець даного відрізка [x0,x];
в). кількість кроків n;
г). значення y0.
3. Обчислюємо величину кроку.
h=(x-x0)/h
4. Привласнюємо у0 першому елементу масива у.
y[0]=y0
5. Обчислюємо розв’язання рівняння, яке обрали. Для цього робимо цикл від 0 до n і при кожнім наступному кроці обчислюємо значення у:
for (int i=0; i<=n; i++)
{
а). обчислюємо i-ий шаг. x1=x0+i*h;
б). обчислюємо значення:
q[i]=h*F(x1,y[i],chose); y1[i+1]=y[i]+(5/12)*q[i].
в). обчислюємо значення:
q1[i+1]=h*F(x1+h,y1[i+1],chose), y1[i+2]=y[i]+(5/12)q[i]+(2/3)*q1[i+1];
q1[i+2]=h*F(x1+h,y1[i+2],chose).
г). обчислюємо значення:
y2[i+2]=y1[i+2]+(2/3)*q1[i+2]-(1/12)*q[i]; q2[i+2]=h*F(x1+2*h,y2[i+2]).
д). обчислюємо значення:
y2[i+3]=y1[i+2]+(2/3)*q1[i+2]-(1/12)*q[i]+(5/12)*q2[i+2],
q2[i+3]=h*F(x1+2*h,y2[i+3]).
е). обчислюємо значення в:
y1[i+3]=y[i]+(5/12)*q[i]+(2/3)*q1[i+2]-(1/12)*q2[i+3],
y[i+1]=y1[i+3].
ж). виводимо значення в[i+3] при його значенні х1:
cout <<x1<<” ”<<y[i+3]
}// кінець циклу при i=n.
6. Кінець програми.
Функція F(x,y) і Yravnen() має такий же вид, як і в методі Рунге-Кутта, Адамса, описані вище.
 |  |  |



y1[i+2]=y[i]+(5/
12)*q[i]+(2/3)*
q1[i+1]
 | |||
 | |||
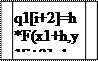

x0, x, n,
y0,chose
 | |||
 | |||


y2[i+2]=y1[i+2]+
(2/3)*q1[i+2]-(1/
12)*q[i]
 | |||
 | |||

 y2[i+3]=y1[i+2]+ |
y2[i+3]=y1[i+2]+ |
(2/3)*q1[i+2]-(1/ ---------------| q2[i+2]
12)*q[i]+(5/12)* |
 |  |

 |
|
-------------------| (5/12)*q[i]+(2/3)*q1[i+2]-(1/12)*q2[i+3]
|
 |  | ||

y[i+3],x1
 | |||
 | |||
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 260; Нарушение авторских прав?; Мы поможем в написании вашей работы!