
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Начало видео-трансляции лекции: 19:30 в 234 аудитории ГК
|
|
|
|
Кредит
Деньги
Логика
План
Ноября 2013 г.
Р А С П И С А Н И Е
установочных лекций для студентов 3 курса заочной формы обучения
НЮИ (ф) ТГУ
| ВРЕМЯ | ПРЕДМЕТ | ПРЕПОДАВАТЕЛЬ | АУД. |
| 14.00-14.30 | Трудовое право | Доц. Архипова ОА | 1 ауд. |
| 14.35-15.05 | Уголовное право | Доц. Минстер МВ | 1 ауд. |
| 15.10-15.40 | Уголовный процесс | Доц. Аверченко АК | 1 ауд. |
| 15.45-16.15 | СОБРАНИЕ | ДЕКАНАТ | 1 ауд. |
| 16.20-16.50 | Земельное право | Доц. Калганова СГ | 1 ауд. |
| 16.55-17.25 | Гражданское право | Доц. Карцева НС | 1 ауд. |
| 17.30-18.00 | Гражданский процесс | Ст.пр. Омельченко ЮП | 1 ауд. |
| 18.05-18.35 | Муниципальное право | Доц. Шерстобоев ОН | 1 ауд. |
ПРИМЕЧАНИЕ: Занятия будут проходить по адресу: ул. Широкая, 33
Зам. директора НЮИ (ф) ТГУ С.В. Азарова
1. Проблема харчування в минулому.
2. Шлях до здоров'я через правильне харчування в наші дні.
2.1 Критерії раціонального харчування
2.2 Незбалансоване харчування
2.3 Недостатнє харчування та його наслідки
3. Клімат і харчування.
Термінологічний словник: раціональне харчування, режим харчування, незбалансоване харчування, йодна недостатність, обмін речовин, вітаміни та мікроелементи, нормальний обмін речовин, дистрофія, ожиріння, атеросклероз, карієс
Усім відомо, що сучасна система освіти базується на вивченні таких наук, як біологія, фізика, механіка, соціологія, що необхідні для забезпечення виробництва й соціального життя. Відрадно, що сьогодні освіта і суспільство робить ще одну спробу на користь людини, запроваджуючи в школах, вищих навчальних закладах науку про здоров'я людини.
Нічого дивного в цьому немає. Високоосвічена сучасна людина може бути неперевершеною в галузі техніки, науки або мистецтва, але так мало знає про те, як потрібно піклуватися про свій власний організм. Зокрема, це стосується нашого повсякденного харчування. Хвороби, обумовлені неправильно організованим харчуванням, серед високоосвічених людей поширені так само, як і серед малоосвічених. Це логічний наслідок нашої системи освіти, в тому числі й шкільної.
1. Проблема харчування в минулому
Ще древні мислителі розуміли, що помірність у їжі — запорука здоров'я і довголіття, а про тих, хто занадто багато їв, говорили: "Ненажера риє собі могилу зубами".
Витоки науки про правильне (здорове) харчування знаходяться в далекому минулому. Наприклад, у Китаї перші лікарі-дієтологи були вже за часів династії Чжоу (бл. ІІ ст. до н е.), вони давали свої рекомендації щодо лікування і профілактики різних захворювань.
Згідно з традиційною медициною Китаю, усі харчові продукти поділялися на холоди: (хань) і гарячі (же), ті, які сприяють збільшенню маси (бу) і схудненню (се) організму.
На сьогодні в Китаї склався традиційний тип харчування, котрий ураховує не тільки сезонні кліматичні зміни, але й географічні, у першу чергу, особливості деяких областей країни. У вологих східних областях перевагу надають гострій, приправленій перцем, їжі. Вона допомагає організмові звільнитися від надлишку вологи. На півдні люблять солодке, на заході — кисле, на півночі їжу добре присолюють.
У цілому традиційна медицина народів Сходу стверджувала, що в харчуванні необхідно враховувати індивідуальні особливості людини. Організм потребує всіх продуктів, але їх співвідношення і кількість повинні змінюватися в залежності від віку, конституції, звичок, клімату.
Тисячоліття тому наші предки вважали, що фізичний стан організму змінюється у відповідності до змін у фізичному стані природи, тобто до сезонних кліматичних змін.
Так, у зимовий час надавали перевагу їжі, що "зігрівала організм". Це яйця, страви, виготовлені із зернових продуктів: пшениці, ячменю, вівса. Вживали гостру їжу — цибулю, молоду редьку, перець; жирні сорти м'яса і риби. Вважалося, що зимою обмін речовин активізується, тому потрібно їсти більше жирної і гострої їжі.
Улітку, навпаки, організм потребує охолодження, і в раціоні повинні переважати "охолоджуючі" продукти: рис, картопля, морква, капуста, редька, фрукти, ягоди, телятина, риба (нежирна).
Говорячи про харчування, не можна забувати про таке. Вибір певних продуктів і страв різними верствами населення не є показником їх реальної поживної цінності. Перевага, як правило, надається їжі, яка швидко викликає почуття насиченості. Прийом їжі — одна з форм соціального самовираження, що відображає стиль життя, матеріальні ресурси, які є у розпорядженні людей.
Кулінарні традиції, що склалися у світових культурах, потрібно розглядати як одну з рис їх самобутності. Загальна трапеза передбачає й загальні відчуття. Тому в багатьох народів різні свята супроводжувалися банкетами.
Існували країни, де в минулі часи харчування було культом. Прийом їжі перетворювався навіть не в насичення, а в ненажерство, яке вважалося за відвагу. Так було в Стародавньому Римі. В той же час у Стародавній Спарті воїни були привчені до їжі бідної, їли один раз на добу, але були сильнішими і здоровішими.
Як правильно харчуватися? Видатний лікар древності Гіппократ так відповідав на це запитання: "Ваша їжа повинна стати ліками, а ваші ліки повинні стати їжею".
Віра в те, що цілющі сили приховані всередині самого організму, який лікує природа, а лікар тільки допомагає, лежала в основі принців лікування Авіценни, Парацельса та інших відомих лікарів минулого.
З середини XVIII століття натуропатія (вживання в їжу натуральних продуктів) як окремий напрямок стала розвиватися в Німеччині. У XX столітті особливого розвитку вона досягла в Швейцарії, Німеччині, Англії, Америці, де стали розроблятися її наукові принципи (Біхнер-Беннер та ін.), а також практичні рекомендації дієтики, тобто науки про раціональне харчування (Г.Шелтон, П.Брегг, А.Шмідт та ін.).
Усі традиційні медичні системи (індійська, китайська, тібетська та ін.) широко використовували харчові рослини для дієтичного харчування і, навпаки, лікарські рослини часто потрапляли на стіл у вигляді страв. Так, наприклад, алтей, лікарську рослину, відому своїми вражаючими властивостями, розводять на Цейлоні як овочеву культуру. В їжу йдуть квіти й листя, а плоди використовують для подолання спраги. А такі відомі зернові і овочеві культури, як рис, пшениця, ячмінь, овес, горох, часник, цибуля, редька, ріпа тощо, широко використовувалися тібетськими медиками з лікувальною метою.
Цілий розділ стародавніх тібетських трактатів "Чжуд-ши" та "Вайдурья-онбо" присвячений рослинам, які використовуються як харчові продукти. Вважалося, що проварена рисова каша зупиняє пронос, вона приємна і задовольняє спрагу, цибуля продовжує сон, збуджує апетит, а часник сприяє лікуванню паразитичних хвороб.
Важко не погодитися з цими на сьогодні практично всім відомими властивостями рисової каші, цибулі, часнику. Але досвід використання рослинної сировини стародавніми медичними системами, не обмежується цими відомими прикладами. Сьогодні не можна стверджувати, що він достатньо вивчений, а те, що вивчене, не завжди береться на озброєння.
Рослини і препарати на їх основі були улюбленими засобами лікування, у тому числі дієтичного, в медицині стародавніх народів.
Так, традиційна медицина Грузії велику увагу приділяла рослинній їжі. В "Усцоро карабадіні читаємо: "Коли пізнаєш хворого, добре подумай, які ліки потрібні, які ні і яка їжа потрібна". У щоденний раціон у Грузії входила велика кількість дикорослих і культивованих рослин: щавель, кропива, черемша, дикий часник, портулак, спаржа, люпин, хміль, петрушка, лебеда, естрагін та ін.
Навряд чи сучасний житель може похвалитися таким асортиментом трав на своєму столі щодня. У кращому випадку навесні дехто урізноманітнює свій стіл першими стравами з кропиви або щавеля і салатом з листків кульбаби. У той же час відомо, що в минулі часи наші предки дуже широко використовували рослини в їжу, в тому числі й дикорослі. Так, у Сибіру в допетровські часи молоді, ще м'які ялинові шишки служили ласощами для людей. Шишки варили з патокою і вживали "для здоров'я". Настої соснових і ялинових бруньок приймали як внутрішній засіб при хворобах дихальних шляхів.
Так, усім відому зараз лікарську рослину хвощ польовий вживали в їжу. Широко було відоме прислів'я: "Хвощ — селянський овоч". Шишковидні утвори на коріннях хвоща, схожі на горшки, у давнину вживали замість ріпи й картоплі. З цими горшками, багатими на крохмаль, жарили яєчню, використовували в сирому вигляді як зелень. Хвощ відомий як,,зілля потрібне “ при цинзі.
Поширене в народі вживання в їжу дикорослих трав пояснюється тим фактом, що ввізні рослини були не доступні через дорожнечу. Так, ціна одного лимона наприкінці XVI-XVII століття була рівна ціні коня.
Досвід використання древніми культивованих і дикорослих рослин з поживними і лікарськими властивостями ще більш цікавий для сучасника тому, що в останній час погляди вчених на харчування значною мірою змінилися.
2. Шлях до здоров'я через правильно харчування в наші дні
Ми живемо у важкий час. Особливо дає про себе знати повсякденна напруга сучасній людині середніх років, яка відображається у швидкому зношенні і руйнуванні організму. Причиною багатьох захворювань, у тому числі хронічних, як стверджують лікарі є неправильне харчування. Список цих захворювань очолюють: атеросклероз, ожиріння, високий кров'яний тиск, цукровий діабет, серцеві напади, рак та ін.
У кожного з нас ще з дитинства виробився певний стереотип харчування. Сьогодні внаслідок економічної нестабільності, зниження матеріального рівня життя багатьох громадян харчовий раціон дуже збіднів. Але прикро те, що ми, з властивою нам наполегливістю все ж ухитряємося їсти не ті продукти, які нам корисні, а навпаки. Та й щодо норм, культури харчування можна поставити багато знаків питання.
Соціально прийняті норми харчування передусім залежать від рівня розвитку, який переживає суспільство, національних традицій, кліматичних умов і, нарешті, індивідуальних особливостей людей: віку, стану здоров'я, способу життя, звичок, релігійних переконань.
Та й раніше, у важкі часи, яких у нас було немало, харчування вважалося достатнім, якщо воно мінімально підтримувало сили організму. Тому найбільшу цінність являли собою висококалорійні продукти — жири, вуглеводи (хліб), м'ясо, необхідні для поновлення енергетичних витрат. Якщо десятки мільйонів у перше тридцятиліття радянської влади стали прямими жертвами голоду, то навіть у відносно "ситих" п’ятдесятих, раціон основної маси народу залишався вкрай далеким від дієтологічно обґрунтованих норм.
Психологічні фактори, свіжа ще пам'ять про пережиті голодні роки підштовхнули до переїдання, тим більше, що вуглеводні продукти (цукор, хліб, мучні вироби) стали нарешті загальнодоступними. У цих умовах стало звичайним "крохмальне ожиріння", яке спричиняється до діабету, серцево-судинних та інших захворювань.
Слід пам'ятати, що неправильно підібрана їжа не тільки впливає на травний тракт, подразнюючи його, викликаючи в ньому запалення, виразки або новоутворення. але також впливає на біохімію організму в цілому. Вираз: "Ми суть те, що ми їмо" — справедливий як у давнину, так і сьогодні. Людина, котра живе на хлібі, м'ясі, м'ясних підливках, картоплі, каві і спиртних напоях, плюс таких приправах, як перець, гірчиця і оцет, кінець-кінцем розплачується хронічними патологічними зрушеннями в організмі.
Неправильне харчування, переїдання, прагнення забезпечити погреби організму в поживних речовинах за рахунок кількості, а не їх якості, спричиняють:
— підвищений механічний і фізичний вплив на опорно-руховий апарат і серцево-судинну систему;
— схильність до варикозного розширення вен, тромбозів, емболії, утрудненого дихання;
— схильність до утворення грижі, серцевої недостатності;
— підвищену схильність до інфекційних захворювань, захворювань шкіри:
— збільшення небезпеки ускладнень і смертності: при хірургічних захворюваннях;
— підвищення тиску;
— захворювання, пов'язані з порушенням обміну речовин;
— діабет;
— захворювання нирок, камені в жовчних протоках:
— нервово-психічні захворювання;
— ускладнення під час вагітності й пологів;
— зменшення тривалості життя та ін.
Існує багато факторів, що впливають на наші стереотипи харчування. Деякі з них ми можемо контролювати, а деякі не підлягають нашому контролю (див. схему № 6). Важливо, щоб кожен навчився розпізнавати ті фактори, які грають певну роль в їхньому житті: позитивну чи негативну. Узагалі кожній людині потрібно усвідомити, що вона може приймати самостійно правильні рішення, зокрема щодо вибору продуктів харчування.
Фактори, що впливають на вибір продуктів харчуванні
|  Вартість Вартість
| 
|  Особисті пристрасті й упередження Особисті пристрасті й упередження
|    
| Етнічне оточення | ||||||

| |||||||||||
 Смак Смак
| Релігія | ||||||||||
| Вплив ровесників | Упаковка | ||||||||||

| Фактори, що впливають на вибір продуктів харчування | ||||||||||
| Енергетична цінність | Зручність у приготуванні | ||||||||||

|   
| ||||||||||
| Емоції | Реклама | ||||||||||
| Склад продукту (вміст білків, жирів, вуглеводів, вітамінів, мікроелементів | Родинні зв’язки і спосіб життя | Настрій | |||||||||
Аналіз негативних стереотипів харчування сучасної людини дозволив визначити такі помилки:
Помилка 1-ша: Ми неправильно вибираємо їжу. Неповноцінність їжі пов'язана з відсутню достатньої кількості вітамінів, що містяться у свіжих овочах та фруктах, клітковини, повноцінного білка, молока і риби. Але в нашому раціоні надмірна кількість білого хліба, тістечок та інших борошняних виробів.
Помилка 2-га: Ми намагаємося вживати багато жирної їжі. При добовій нормі 80 г, людина з'їдає в середньому 132 г жиру, що створює реальну небезпеку для здоров'я.
Помилка 3 - тя: Ми нехтуємо природними запасами рідини — водою. Натомість вводимо в організм багато алкоголю і солодких напоїв.
Помилка 4 - та: Ми неправильно готуємо їжу. Зловживаємо кухонною сіллю, жареним і вареним навіть тоді, коли цього можна було б уникнути.
Помилка 5 - та: Ми харчуємося без урахування досягнутого віку. Дорослі не лімітують прийом їжі і не привчають до цього дітей. Люди похилого віку забувають про те, що їм необхідно обмежити харчування через зменшення витрат енергії.
Помилка 6 - та: Ми погано знаємо про основи здорового харчування. Наука має велику кількість даних про раціональне харчування, але більшість людей, нажаль, користуються ними мало.
3. Клімат і харчування
В умовах суворого холодного клімату вимагається один вид харчування, а в жаркому кліматі — інший. Деякою мірою можна погодитися з тим, що люди бувають здоровіші, коли їдять те, що їли їх предки.
Холодна мої ода або холодний клімат передбачають сніданки, обіди і печері, складені з калорійних продуктів, які легко засвоюються. Не слід вживати на сніданок печені пиріжки і м'ясо, як це роблять деякі американці й нанайці.
Обіди в умовах холодного клімату можуть складатися з двох страв: багатої гарячої страви овочевого супу; компоту; звареного рису або іншої круп'яної або білкової страв.
Страви на вечерю повинні містити рівну кількість свіжої сирої їжі та їжі, яка зварена на пару або у воді.
Жарка погода і теплий клімат вимагають холодної їжі. Людина, котра живе в жаркому кліматі, вживає в їжу у великій кількості сирі фрукти.
Без сумніву, в жаркому кліматі не слід харчуватися жирною їжею: страви з цукром також не рекомендуються. У літній період у спеку не потрібно зовсім вживати м'ясо, навіть горіхи не бажані.
Солодкі фрукти, такі, як фініки, фіги та ізюм, не рекомендується використовувати в їжу плітку. їх можна їсти тільки на вечерю, коли не так спекотно. Фрукти, особливо ті, які захищені щільною шкірочкою, такі, як апельсини, виноград, ананаси і дині, не шкідливі. Фрукти, зрозуміло, вживають тільки свіжі й чисті.
Люди, які дотримуються такої дієти, хоч і живуть у тропічному кліматі, не хворіють інфекційними захворюваннями.
Розумне харчування населення, яке відповідає клімату і погоді, зробить будь-яке суспільство більш здоровим і щасливим.
Питання для самоперевірки
1. Який підхід був характерним у створенні норм харчування в давнину? Відповідь обґрунтуйте.
2. Які тенденції переважають у виборі продуктів харчування сучасною людиною?
3. Прокоментуйте схему "Фактори, що впливають на вибір продуктів харчування ".
4. Які патологічні зрушення в організмі спричиняються переїданням, вибором продуктів за кількістю, а не за якістю тощо?
5. Назвіть помилки, проаналізувавши негативні стереотипи нашого повсякденного харчування. Чи характерні вони для вас?
6. Який існує взаємозв 'язок між кліматом і вибором продуктів харчування?
Література
1. Григорян Г. Была ли диетотерапия в прошлом? Чего бы такого поесть...//Твое здоровье. — 1991 —№ l.-С. 3-8.
2. Лозинский B.C. Учитесь быть здоровыми. — К., 1993. — С. 40-43.
3. Мсдкова И.Л., Павлова Т.Н. Пища, которая лечит. — М., 1995 — С. 97-98.
4. Шмидт A.A. Вопросы питания здорового и больного человека. — Рига, 1960. — 68 с.
Логика – это нормативная наука о формах и приемах интеллектуальной познавательной деятельности, осуществляемой с помощью языка.
Познание – процесс отражения в человеческом мозге некоторой информации. Познание бывает:
· Чувственное
· Рациональное (вербальность, абстрактность, целенаправленность)
Язык – знаковая система, предназначенная для обработки, фиксирования, передачи и хранения информации.
Естественный язык создается в историческом процессе, основная задача – общение.
Искусственный язык создается целенаправленно для решения определенных задач.
Объектный язык – это тот язык, которым ведется какое-либо исследование.
Метаязык – тот язык, который используется для изучения другого языка.
Знак – это объект, который выступает в качестве представителя какого-либо другого объекта. Характеристики знака:
· Значение – тот самый объект, представителем которого является данный знак
· Смысл – информация о представляемом объекте, которую несет сам знак или которая связывается с ним в процессе человеческого общения или познания.
С точки зрения
1. значения знаки бывают:
· пустые – на заданной предметной области нет ни одного объекта, представителем которого выступал бы этот знак
· непустые – на заданной предметной области знак выступает представителем хотя бы одного объекта
2. смысла знаки бывают:
· описательные – знак сам несет информацию о представляемом объекте
· неописательные – информация связывается в процессе человеческого общения/познания
Семиотика – наука о знаках. Делится на:
· Синтактика – изучает отношения между самими знаками
· Семантика – изучает отношения между знаком и представляемым им объектом
· Прагматика – изучает отношения между знаком и его интерпретатором
Классическая теория высказываний (КЛВ)
КЛВ – логическая теория, содержащая один тип нелогических символов – пропозициональные переменные, и один тип логических символов – пропозициональные связки.
Высказывание – повествовательное предложение, о котором однозначным образом можно утверждать, что оно истинное или ложное.
Язык КЛВ:
· Алфавит
o p, q, r, s, p1, … - пропозициональные переменные
o ˥, &, V,  ,
,  , V – пропозициональные связки
, V – пропозициональные связки
o), (- технические символы
˥ - отрицание (не)
& - конъюнкция (и)
V – дизъюнкция (или)
V – строгая дизъюнкция (либо, либо)
 - импликация (если, то)
- импликация (если, то)
 - эквивалентность (тогда и только тогда, если и только если)
- эквивалентность (тогда и только тогда, если и только если)
· Определение ППФ
o Всякая пропозициональная переменная – это ППФ
o Если A – ППФ, то ˥A – так же ППФ
o Если A и B – ППФ, то (A&B), (AVB), (A V B), (A B), (A
B), (A B) – ППФ
B) – ППФ
o Ничто иное не является ППФ
Пример: если гора не идет к Магомету, то Магомет идет к горе.
P – гора идет к Магомету
Q – Магомет идет к горе
˥P Q
Q
Таблицы истинности
1 = истинно
0 = ложно
| A | B | A&B (*) | AVB (+) | A V B (-) | A B (≤) B (≤)
| A B (=) B (=)
|
Всего строк 2n где n – это число различных пропозициональных переменных, вошедших в формулу.
Результирующий столбец таблицы находится под главным знаком формулы.
Виды формул:
1. Тождественно-ложные (противоречия) – если и только если в каждой строке результирующего столбца она принимает значение «ложь» (0).
2. Выполнимые – если и только если она принимает значение «истина» хотя бы в одной строке результирующего столбца.
3. Собственно выполнимая – если и только если в каждой строке результирующего столбца она принимает значение «истина»
3 закона КЛВ
1. Закон тождества A A
A
2. Закон исключенного третьего AV˥A
3. Закон противоречия ˥(A&˥A)
4. Закон контрпозиции (A B)
B)  (˥B
(˥B ˥A)
˥A)
Отношения между формулами:
· Фундаментальные (основные) – формулы некоторого множества Г находятся в отношении совместимости по ложности если и только если хотя бы в одной строке их совместной таблицы они одновременно принимают значение ложь
· Вспомогательные – формулы некоторого множества Г находятся в отношении совместимости по истинности если и только если хотя бы в одной строке их совместной таблицы они одновременно принимают значение «истина»
· Из множества формул Г логически следует формула B (Г|=B) если и только если в их совместной таблице не находится такой строки, в которой все формулы из Г одновременно принимают значение «истина», а формулы B – ложь.
· Формулы A и B находятся в отношении контрарности если и только если они совместимы по ложности и не совместимы по истинности
· Формулы A и B находятся в отношении субконтрарности если и только если они совместимы по истинности и не совместимы по ложности
· Формулы A и B находятся в отношении контрадиктности если и только если они не совместимы по ложности и не совместимы по истинности или не совместимы по ложности
· Формула B находится в отношении подчинения к формуле A если и только если из формулы A|=B, а из формулы B не следует A
· Формулы A и B находятся в отношении эквивалентности если и только если A|=B и B|=A
· Формулы A и B находятся в отношении независимости если и только если они совместимы по истинности, совместимы по ложности и не следуют друг из друга
Классическая логика предикатов (КЛП)
Язык КЛП:
· Алфавит
o a, b, c, d, a1 … - индивидуальные константы (имена собственные)
o x, y, z, x1… - индивидуальные переменные (имена нарицательные)
o f′, g′ - функторы
o P1, Q1, R1, S1, R2 – предикаты
o ˥, &, V,  - пропозициональные связки
- пропозициональные связки
o Ǝ, 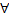 - кванторы
- кванторы
o), (- технические символы
Предметные функторы – термины, с помощью которых в языке представляются предметные функции (с помощью предметных функторов – выражения).
Пример: Аристотель – a
отец Аристотеля - f′(a)
Предикаты – термины, выражающие в языке предметно-истинностные функции (свойства и отношения)
· Определение правильно построенного терма:
o Всякая индивидуальная константа – это ППТ
o Всякая индивидуальная переменная – это ППТ
o Если Фn – n-местный предметный фактор, а t₁, t₂, t₃, …, tn – правильно построенные термы, то Фn (t₁, t₂, t₃, …, tn) – это ППТ
o Ничто иное не является ППТ
· Определение правильно построенной формулы (ППФ)
o Если П - n-местный предикат, а t₁, t₂, t₃, …, tn – это ППТ, тогда П n(t₁, t₂, t₃, …, tn) – ППФ
o Если A – ППФ, то ˥A – ППФ
o Если A и B – ППФ, то (A&B), (AVB), (A B) – ППФ
B) – ППФ
o Если A и B – ППФ, α – индивидуальная переменная, то ƎαA, 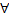 αA – ППФ
αA – ППФ
o Ничто иное не является ППФ
Пример:
4 = a 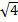 - f1(a)
- f1(a)
5 = b 4+5 - g2(a, b)
√ = f1 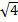 +5 - g2(f1(a), b)
+5 - g2(f1(a), b)
+ = g2 (4+4)+(5+5) - g2(g2(a, a), g2(b, b))
В формулах вида 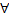 αA и ƎαA формула A называется областью действия квантора по переменной α.
αA и ƎαA формула A называется областью действия квантора по переменной α.
В произвольной формуле каждая индивидуальная переменная имеет некоторое число вхождений.
Вхождение индивидной переменной в некоторую формулу называется связанным, если оно следует непосредственно за квантором или находится в области действия квантора по данной переменной, в противном случае вхождение переменной в формулу называется свободным.
Индивидная переменная называется свободной в некоторой формуле, если существует по крайней мере одно свободное вхождение в эту формулу.
Терм называется замкнутым, если он не содержит в своем составе ликвидных переменных.
Формула называется замкнутой, если никакая индивидная переменная не является в ней свободной.
1. Закон подчинения
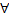 αA
αA ƎαA
ƎαA
2. Закон противоречия
˥ (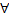 αA&˥
αA&˥ 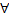 αA)
αA)
3. Закон непустоты предметной области
4. ƎαA V ˥ ƎαA
Рассуждение – это логическая процедура последовательного перехода от одних высказываний, принятых в качестве посылок, к другим высказываниям. Каждый шаг такого перехода осуществляется по какому-либо правилу вывода. Последняя формула рассуждения – заключение.
Дедуктивное рассуждение – рассуждение, в котором между высказываниями, принятыми в качестве исходных, и заключением сохраняются отношения логического следования.
Аналитические таблицы (АТ)
Логические теории бывают разрешимыми (КЛВ) и неразрешимыми (КЛП).
Теория называется разрешимой если существует эффективная процедура (алгоритм), позволяющая для любой формулы языка данной теории в конечное число шагов решить вопрос о том, является ли эта формула законом теории или нет. В противном случае теория называется неразрешимой.
Метод от противного: |=A допустим: ˥A
Особенности АТ
1. Аналитическая таблица состоит из отмеченных формул (к которым добавили знак t или f)
2. АТ двумерна – это дерево отмеченных формул. Цепь АТ – последовательность, без пропусков, вхождений отмеченных формул, начинающаяся с самой верхней формулы таблицы (кроме дерева) до 1 из самых нижних формул.
Таблица, соответствующая одному шагу рассуждений от противного, содержит одну начальную цепь формул и выражает исходные допущения данного рассуждения (т. е. антитезис).
Правила редукции:
| t (A&B) | f (A&B) | |
| t A, t B | f A | f B |
| t (A V B) | f (A V B) | |
| t A | t B | f A, f B |
t (A  B) B)
| f (A  B) B)
| |
| f A | t B | t A f B |
| t ˥A | f ˥A | |
| f A | t A | |
t 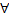 αA (α) αA (α)
| f 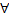 αA (α) αA (α)
| |
| t A (k) где A (k) – результат замены всех свободных вхождений α в A на произвольной замкнутый терм k | f A (k) где A (k) – результат замены всех свободных вхождений α в A на произвольной замкнутый терм k, который не содержится в отмеченных формулах цепи | |
| t ƎαA (α) | f ƎαA (α) | |
| t A (k) | f A (k) |
Аналитическая таблица – конечное или бесконечное дерево отмеченных формул. Цепь называется замкнутой, если в ней встречается две отличные формулы tC и fC. АТ называют замкнутой, если каждая ее цепь является замкнутой.
Формула A является общезначимой (|=A) если и только если существует замкнутая аналитическая таблица, начальная цепь которой начинается с отмеченной формулы fA.
A₁, A₂, A₃, …, An |=B если и только если существует замкнутая аналитическая таблица, начальная цепь которой начинается с отмеченных формул tA₁,t A₂,t A₃, …,t An fB.
Натуральные исчисления. Исчисления высказываний.
Правила редукции (вывода):
1. &в: 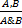
2. Vв: 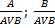
3.  в:
в: 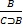 (последняя посылка вывода)
(последняя посылка вывода)
4. &и: 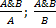
5. Vи: 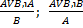
6. ˥в: 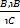
7.  и:
и: 
8. ˥и: 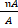
Вывод – это непустая конечная последовательность формул C₁, C₂, C₃, …, Cn, удовлетворяющая следующим условиям:
1. Каждая Ci является либо посылкой, либо получена из предыдущей формулы по одному из правил вывода
2. Если в выводе принимались правила  B или ˥B, то все формулы, начиная с последней посылки вплоть до результата применения этого правила, считаются исключенными из вывода и не участвуют в дальнейшем построении вывода.
B или ˥B, то все формулы, начиная с последней посылки вплоть до результата применения этого правила, считаются исключенными из вывода и не участвуют в дальнейшем построении вывода.
Доказательство – вывод из пустого множества не исключенных посылок.
· B – введение импликации
˥B – введение отрицания
Силлогистика
Аристотель (384 - 322 до н. э.)
Силлогистика – это логическая теория, изучающая простые категорические атрибутивные высказывания (ПКАВ) и отношения между ними.
Состав ПКАВ:
1. Квантор
2. Термины:
· S – субъект высказывания, логическая подлежащее, тот объект, о котором идет речь
· P – предикат, логическое сказуемое, то, что говорится о субъекте, предицируется субъектом
3. Связка (есть, является, суть, -)
Пример: Все мишки любят мед
 | |||
 | |||
Виды высказываний
I. По количеству:
a. единичные – субъект которых указывает ровно на один предмет
b. множественные – субъект которых указывает более чем на один предмет
i. общие – субъект говорит обо всех элементах класса S
ii. частные – субъект говорит о некоторых (возможно, всех) элементах класса S
II. По качеству:
a. Утвердительные – перед связкой не стоит частица «не»
b. Отрицательные – перед связкой стоит частица «не»
A ff i rmo - утверждаю
N e g o – отрицаю
Отсюда обозначения (гласные буквы приведенных выше слов)
Общеутвердительные – все S являются P (a)
общеотрицательные - все S не являются P (e)
частноутвердительные - некоторые S являются P (i)
частноотрицательные - некоторые S не являются P (o)
единичноутвердительные – a является P
единичноотрицательные – a не является P
На единичные букв не хватило. Ну и ладно, всё равно это частный случай общих.
Язык силлогистики
· Алфавит
o S, P, M, S₁ - термины
o a, e, i, o – логические константы
o ~ - терминное отрицание («не»)
o ˥, &, V,  - пропозициональные связки
- пропозициональные связки
o), (- технические символы
· Определение правильно построенного терма (ППТ)
o Всякий термин является ППТ
o Если α – ППТ, то ~α – ППТ
o Ничто иное не является ППТ
· Определение ППФ
o Если α и β – это ППТ, то α a β, α i β, α e β, α o β – ППФ
o Если A – ППФ, то ˥A – ППФ
o Если A и B – ППФ, то (A&B), (AVB), (A B) – ППФ
B) – ППФ
o Ничто иное не является ППФ
Модельные схемы
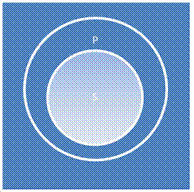
I. Высказывание «Все S являются P» истинно тогда и только тогда. Когда классы S и P находятся в одном из следующих отношений: S+aP-


II. Высказывание «Все S не являются P» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: S+eP+


III. Высказывание “Некоторые S являются P» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: S-iP-

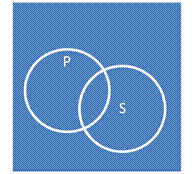

 (закрашено пересечение)
(закрашено пересечение)
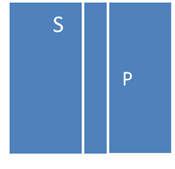
IV. Высказывание «Некоторые S являются P»» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: S-oP+




 (закрашено S без P)
(закрашено S без P)
V. Высказывание «a является P»» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: a+P-

VI. Высказывание «a не является P»» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: a+P+
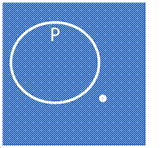
Термин считается распределенным если и только если на всех модельных схемах, которые являются условием истинности того высказывания, в которое он входит, он полностью заштрихован или полностью не заштрихован, в противном случае термин считается нераспределенным.
Единичные высказывания являются вырожденным случаем общих.
Формула A является законом силлогистики если и только если она истинна на всех модельных схемах.
Из множества формул Г логически следует формула B если и только если не найдется такой модельный схемы, на которой все формулы из Г – истинны, а формулы B ложны.
Простой категорический силлогизм (ПКС) – умозаключение, в котором на основании некоторого отношения между терминами P и M, а так же терминами S и M делают вывод о наличии определенного отношения между S и P.
Состав ПКС
S – это субъект заключения, меньший термин, посылка, в которой он находится. Называется меньшей.
P – это предикат заключения, больший термин. Посылка, в которой он находится, называется большей.
M – это средний термин, встречается в обеих посылках, но никогда в заключениях.
Модус – разновидность силлогизма, которая определяется видами высказываний, вошедших в этот силлогизм.
Силлогизм является верным если и только если он удовлетворяет следующим условиям:
I. Правило посылок:
1. Хотя бы одна посылка должна быть утвердительной.
2. Если обе утвердительные, то и заключение должно быть утвердительным.
3. Если одна из посылок отрицательная, то и заключение – отрицательное.
II. Правило терминов:
1. Средний термин должен быть распределен хотя бы в одной из посылок.
2. Если термин распределен в заключении, то он должен быть распределен и в посылке.


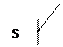

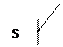

 Пример: Настоящие йогурты содержат живые бактерии.
Пример: Настоящие йогурты содержат живые бактерии.
Йогурты Danone содержат живые бактерии, значит, йогурты Danone – настоящие йогурты.
+PaM-
+SaM-
+SaP-
Силлогизм неверен.
Энтимема – простой категорический силлогизм, у которого пропущена одна из посылок или заключение.
Виды энтимем:
· Корректные – восстанавливаются до правильного силлогизма с истинными посылками
· Некорректные – не восстанавливаются до правильного силлогизма, или восстанавливаются, но одна из посылок – ложная

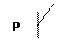

 Пример: Все кролики едят капусту. Все кролики – вегетарианцы.
Пример: Все кролики едят капусту. Все кролики – вегетарианцы.
+SaM-
+MaP-
+SaP-
Все, кто ест капусту – вегетарианцы. – ложь => энтимема некорректна
Непосредственные умозаключения – это умозаключения, в которых вывод делается на основании одной только посылки.
I. Выводы по логическому квадрату – это непосредственные умозаключения со следующей структурой
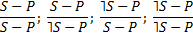
| контрарность | ||
| п о д ч и н е н и е | п о д ч и н е н и е | |
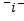
| субконтрарность | 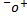
|
1. 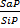
2. 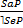
3. 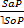
4. 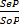
5. 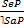
6. 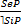
7. 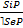
8. 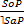
9. 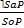
10. 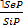
11. 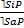
12. 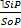
13. 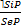
14. 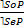
15. 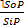
16. 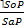
II. Обращение – это непосредственное умозаключение со следующей структурой
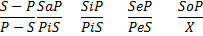
III. Превращение – это неполное умозаключение со следующей структурой
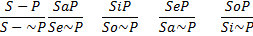
IV. Противопоставление субъекту – это непосредственное умозаключение со следующей структурой (обращение - превращение)
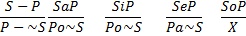
V. Противопоставление предикату – это непосредственное умозаключение со следующей структурой (превращение – обращение)
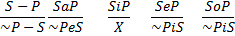
VI. Противопоставление субъекту и предикату - это непосредственное умозаключение со следующей структурой (превращение – обращение – превращение)
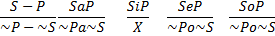
Понятие
Понимать термин – значит по любому предъявленному предмету уметь определять, подпадает ли он под данный термин или нет.
Понятие – это мысль, в которой на основании некоторого признака выделяются из универсума и обобщаются в класс все предметы, обладающие этим признаком.
αA (α) – универсалия.
Предмет α из универсума U такой, что он обладает признаком A (α).
Универсум U, по которому пробегает α, называется родом, а признак A (α) – видовым отличием.

 Пример: человек, изучающий логику
Пример: человек, изучающий логику
A (α) – содержание

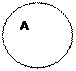
 Объем W α A (α)
Объем W α A (α)
U - человек
Элемент объёма
У всякого понятия есть две основные характеристики: содержание и объем.
Содержание понятия – это тот самый признак, на основании которого предметы выделяются из универсума и обобщаются в класс.
Объем понятия – это класс всех тех предметов, которые обладают признаком, указанным в понятии.
 α A (α)
α A (α)
Объем W α A (α) содержание A (α)
Виды понятий
I. По объему:
· Пустые – пустым считается понятие, в объеме которого нет ни одного элемента
· Непустые – непустым считается понятие, в объеме которого есть хотя бы один элемент
üЕдиничные – в объеме понятия ровно один элемент
üОбщие – в объеме понятия больше одного элемента
§ Универсальные – объем понятия совпадает с универсумом
§ Неуниверсальные – объем понятия меньше универсума
· Конкретные – конкретным считается понятие, элементами объема которого являются отдельные предметы или их множества
· Абстрактные – абстрактным считается понятие, элементами объема которого являются свойства, отношения или их множества.
· Собирательные - собирательным считается понятие, элементами объема которого являются множества.
· Несобирательные - несобирательным считается понятие, элементами объема которого являются отдельные предметы, свойства, отношения
II. По содержанию:
· Простые – признак не содержит логических констант (пропозициональных связок и кванторов).
· Сложные – содержат хотя бы одну логическую константу.
· Положительные – признак не содержит пропозициональные связки и отрицание.
· Отрицательные – признак содержит отрицание.
· Относительные – признак является реляционным свойством (признак не содержит свободным переменных).
· Безотносительные – признак не является реляционным свойством.
Булевы операции над объемами и понятиями.
1. Пересечения 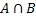
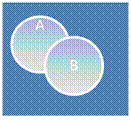
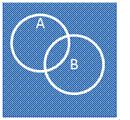
Пересечь два множества, являющиеся объёмами понятий A и B – значит указать объем нового понятия, элементами которого являются те и только те объекты, которые одновременно принадлежат и объему A, и объему B.
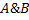
2. Объединение 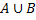
Объединить два множества, являющиеся объёмами понятий A и B – значит указать объем нового понятия, элементами которого являются те и только те объекты, которые принадлежат или объему A, или объему B.
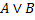
3.  Вычитание
Вычитание 
Вычесть из множества, являющиеся объёмом понятия A, понятие, множество, являющееся множеством понятия B – значит указать объем нового понятия, элементами которого являются те и только те объекты, которые принадлежат объему A, но не принадлежат объему B.
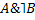
4.  Взятие дополнения
Взятие дополнения 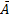
Взять дополнение к множеству A, значит указать объем нового понятия, элементами которого являются те и только те объекты, которые не принадлежат объему A.
˥A
1. 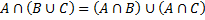

2. 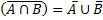
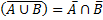
3. 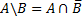
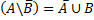
Два понятия α A (α) и α B (α) считаются сравнимыми, если и только если их универсумы совпадают. В противном случае понятия считаются несравнимыми.
3 фундаментальных отношения:
1. α A (α) и α B (α) находятся в отношении совместимости если и только если для их объемов верно, что в них имеется по крайней мере один общий элемент.
2. α B (α) находится в отношении включенного понятия α A (α) если и только если для их объемов A и B верно, что каждый элемент из B является так же элементом A.
3. Два понятия α A (α) и α B (α) находятся в отношении исчерпывания если и только если для их объемов A и B верно, что каждый элемент универсума является элементом A или элементом B.
Вспомогательные отношения.
1.  Равнообъемность
Равнообъемность
1. Совместимость
2. Обоюдная включенность
3. Неисчерпывание
2. 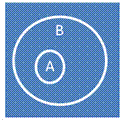 A подчиняется B
A подчиняется B
1. Совместимость
2. A включается в B
3. Неисчерпывание
3. 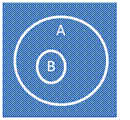 B подчиняется A
B подчиняется A
1. Совместимость
2. B включается в A
3. Неисчерпывание
4.  Дополнительность
Дополнительность
1. Совместимость
2. Невключение
3. Исчерпывание
5. 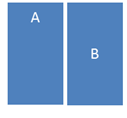 Противоречие
Противоречие
1. Несовместимость
2. Невключение
3. Исчерпывание
6. 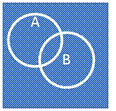 Пересечение
Пересечение
1. Совместимость
2. Невключение
3. Неисчерпывание
7. 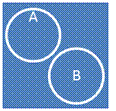 Соподчинение
Соподчинение
1. Несовместимость
2. Невключение
3. Неисчерпывание
Операции над объемами понятий
1. Обобщить непустое понятие α A (α) значит указать такое понятие α B (α), что для их объемов A и B будет верно включение первого во второе.
Предел обобщения – универсальное понятие.
2. Ограничить непустое понятие α B (α), значит указать такое непустое понятие α A (α), что для их объемов A и B будет верно включение первого во второе.
Предел ограничения – единичное понятие.
3. Под делением непустого понятия α B (α) понимают переход от объема этого понятия B к системе 
α B (α) – делимое понятие
S – система членов деления
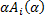 - член деления
- член деления
основание деления – это та характеристика элементов из объема делимого понятия, модификация которой и вызывает систему членов деления S.
Деление считается правильным если и только если оно удовлетворяет следующим условиям:
1. Каждый член деления является видовым по отношению к делимым понятиям.
2. Члены деления попарно несовместимы.
3. Объединение всех членов деления равно объему делимого понятия.
4. Каждый член деления не пуст.
5. Деление должно проводиться по одному основанию.
Виды деления:
· Дихотомическое
· По видоизменению основания
Определение
Определение – это логическая процедура придания точного смысла языковым выражениям (терминам языка).
Основная функция определения – задание значения для определяемого термина.
3 приема, сходных с определением:
1. Остенсивное «определение» (указание на предмет)
2. Описание (простое перечисление известных характеристик предмета)
3. Сравнение (одного предмета с другим)
Требования, предъявляемые к определению
1. Ясность и четкость – определение должно даваться через знакомые термины, не должно содержать лишней информации.
2. Система определений не должна содержать порочного круга (не должна замкнуться).
Виды определений: явные и неявные
· 
 Явные – задаются лингвистической конструкцией следующего вида:
Явные – задаются лингвистической конструкцией следующего вида:


В определяемой части содержится определяемый термин.
Виды явных определений в зависимости от того, к какой языковой категории принадлежит A:
1. Определение имени
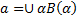 – сложное имя
– сложное имя
a – тот самый α который обладает признаком B(α)
2. 
 Определение универсалии
Определение универсалии
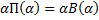
3. Определение высказывательной формы
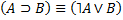
4. Определение функционального выражения
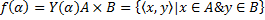
α – индивидуальная константа или индивидуальная переменная
П – предикат
f – функтор
Определяемый термин не должен содержаться в определяемой части.
Явные определения:
· Родовидовые
o Генетические – B(α) указывает на способ порождения предикатов
o Квалифицированные - B(α) указывает на существования характеристики или структурные особенности предмета
o Целевые - B(α) указывает на значение предмета
o Операциональные - B(α) указывает на процедуру, с помощью которой можно определить подпадает ли данные предмет под неявное определение
· Неродовидовые
Определения универсалий бывают перечислительными определениями.
Определение имени – определение имени через гипостазирование.
I. Обобщающая абстракция
отцовство - «x отец y»
<x, y> (мужчина x & родители (x, y))
II. Изолирующая абстракция
«быть отцом»
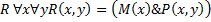
III. Гипостазирование: имя отношения «отцовство»
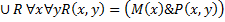
IV. Определение
отцовство = 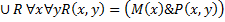
Закон
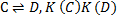
Неявные определения
Задаются лингвистической конструкцией следующего вида:
A есть то, что удовлетворяет условию 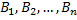
Особенности неявного определения:
1. 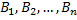 - высказывания, могут быть истинными или ложными
- высказывания, могут быть истинными или ложными
2. Определяемый термин может содержаться в определяемой части
3. Не действует принцип замены по дифиниции
Бывают:
· Индуктивные (с их помощью задаются множества)
1. Базис индукции
2, 3, 4…n индуктивные шаги
n+1 ничто иное не является A
· Рекурсивные – с их помощью задаются функции
1. Базис рекурсии
2. Рекурсия
…
x+0=x
· Аксиоматические (фундаментальные понятия)
Еще определения бывают:
· Контекстуальные – определяемая или определяющая часть содержит контекст употребления данного определения.
· Неконтекстуальные
А так же:
· Реальные
С семантической точки зрения, реальное определение – это то, которое дается действительно существующему объекту или его характеристикам
С прагматической – которое дается для уточнения смысла.
· Номинальные – выражает собой простую конвекцию называть тот или иной объект каким либо словом.
Подробнее об индукции советую прочитать в работе А. И. Ноткина «Учебник по индукции»
1.2 Денежное обращение и его структура
1.2.1 Сущность денежного обращения
Денежное обращение – движение денег в наличных и безналичных формах, обслуживающее реализацию товаров и нетоварные платежи и расчеты в хозяйстве. Денежное обращение является результатом товарного производства. По своей структуре денежное обращение делится на две сферы:
- наличную;
- безналичную.
Наличное денежное обращение – движение наличных денег, обслуживается бумажными деньгами, разменной монетой, банкнотой. В развитых капиталистических странах банковские билеты выпускаются ЦБ и составляют подавляющую часть наличного денежного обращения. Незначительная часть выпуска денег приходится на Казначейство, которое выпускают, в основном, монеты и мелкокупюрные денежные бумажные знаки – казначейские билеты. Безналичное денежное обращение – движение денег без наличного оборота: банковские депозиты на счетах клиентов, использование которых осуществляется с помощью чеков, кредитных карточек, электронных переводов. В денежном обращении так же участвуют: векселя, сертификаты и другие обязательства. Между наличным денежным оборотом и безналичным денежным оборотом существует тесная взаимосвязь, т.к. деньги переходят из одной формы в другую. Соотношение между наличным и безналичным оборотом зависит от многих факторов. Так, например, в некоторых странах наличный оборот составляет 10%, а безналичный – 90%.
1.2.2. Законы денежного обращения
Закон денежного
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 329; Нарушение авторских прав?; Мы поможем в написании вашей работы!
