Рассмотрим более подробно второй закон Снелля

Угол q меняется от 0 до p/2 (p/2 – предельное значение).

Угол падения, при котором q = p/2, назовём критическим:

,

это возможно, если .

При j > j_кр правая часть становится больше единицы. Если q – вещественный, это невозможно.

Будем полагать: .

Тогда: .

Чтобы sin q >1 достаточно: и 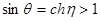, а cosq – мнимый.

С учётом этого при любом h ¹ 0:

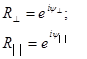
То есть средняя плотность потока энергии одинакова в падающей и отражённой волнах.

Поле в первой среде (после того, как за скобки вынесли exp(iy_^/2)):

;

Итак, в первой среде ЭМП имеет структуру плоской волны, распространяющейся вдоль поверхности раздела (вдоль z) – направленная волна.

Поверхности равных фаз – плоскости, перпендикулярные Z.

Амплитуды E и H зависят от X и от j.

Поверхности равных амплитуд–плоскости, перпендикулярные X.

Эта волна - неоднородная плоская волна, у которой есть продольная составляющая Hz.

(для волны с параллельной поляризацией–Ez).

Фазовая скорость:

,

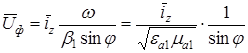то есть 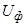больше , но меньше . Причём, чем больше j, тем меньше .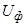

Длина волны вдоль Z: .

Изменение Е и Н вдоль оси Х имеет характер стоячей волны в первой среде: .

Поперечные составляющие изменяются в фазе, а продольная сдвинута на 90°, в результате комплексный вектор Пойнтинга:

Знак ’+’ – перпендикулярная поляризация.

Знак ‘_’ - параллельная поляризация.

В среднем энергия распространяется только вдоль оси Z, а в перпендикулярном по отношению к Z направлении – только реактивный поток энергии:

Рассмотрим поле во второй среде:

Так как cos q – мнимая величина, то:

где

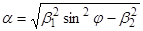
при j > j_кр a – вещественная величина.

Знак ’’–’’ чтобы поле не росло до бесконечности (невозможно физически).

Для поля во второй среде:

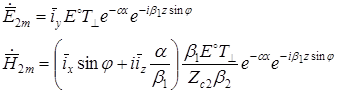
Итак, во второй среде электромагнитное поле имеет структуру плоской неоднородной волны, распространяющейся вдоль оси Z.

Поверхности равной фазы и амплитуды взаимно перпендикулярны.

Энергия распространяется в среднем вдоль z, а вдоль x она убывает по экспоненциальному закону.

Такую волну называют поверхностной.

Любая из поверхностей X_n = const могла быть заменена на металлическую – это не изменит картины.

Поток энергии на плоскостях X_n = const - отсутствует (n = 1,2...).

Если вместо двух диэлектрических сред – граница раздела металл (идеально проводящий) и диэлектрик, то .

Тогда R_^= -1; T_^= 0; y_^= p;

R_êê= 1; T_êê= 0; y_êê= 0;

при любом угле падения j.

Структура поля в первой среде та же, 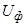и – не меняются, а во второй среде поля нет.

На границе раздела с поглощающей средой можно воспользоваться полученными выражениями, если предположить, что b₂ – комплексная величина: .

Тогда sinq – тоже комплекс, то есть q – не геометрический угол, под которым распространяется преломлённая волна.

Введём обозначения:

a, b_x, b_z – вещественные.

Для нормально поляризованной волны:

То есть в поглощающей среде – поле – плоская волна и если j ¹ 0 – неоднородная.

Поверхности равной амплитуды:

Х = const.

Поверхности равной фазы:

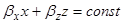
Во второй среде направление распространения образует угол q_Д с осью x.

q_Д - истинный (действительный) угол: .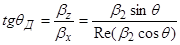

(волна расположена перпендикулярно поверхностям равных фаз).

Во второй среде амплитуда убывает по экспоненте, причём во второй среде есть продольная составляющая.

Для параллельной поляризации то же самое.

Практически важный случай .

Например, металлы: , тогда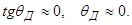

То есть при любом угле падения j на поверхность хорошо проводящей среды преломлённая волна распространяется практически вдоль нормали к границе раздела.

Плоскости равных фаз и амплитуд практически совпадают - волна однородная.

Волна - поперечная, причём Е и Н сдвинуты по фазе на .

Так как амплитуда быстро убывает, то поле есть практически в тонком поверхностном слое (явление поверхностного эффекта).

По закону Ома: J = dE, весь ток сосредоточен возле поверхности. Эффективное сечение меньше геометрического, а активное сопротивление на ВЧ может быть во много раз больше, чем по постоянному току (проводник можно выполнить в виде трубы).

Используют математическую модель, полагают, что ток течёт в виде бесконечно тонкого слоя:

,

Z_СМ - поверхностное сопротивление проводника, d - глубина проникновения.

Это выражение было получено на основе граничных условий Леонтовича–Щукина.

Особенность в том, что они выражают соотношение между векторами электромагнитного поля вблизи границы с реальными металлическими телами через параметры металла, без учёта поля в нём.

Мы уже определили, что в хорошо проводящей среде поле распространяется вдоль нормали к границе раздела:

.

На границе раздела:

.

Векторы Е и Н параллельны границе раздела, следовательно:

,

так как

,

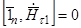то вместо 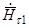можно использовать полный :

.

На поверхности реального проводника 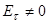и, хотя она очень мала (), она определяет нормальную составляющую П (поток энергии, уходящий в металл).

Составляющую в расчётах учитывают только тогда, когда рассчитывают потери.

Если граница раздела не плоская, то дополнительное условие - радиус кривизны должен превышать глубину проникновения.

Отражение от системы слоёв

На занятие решим задачу отражения от слоя.

Здесь приведём выражения для коэффициента отражения от системы слоёв.

Полагаем, что между двумя полубесконечными средами находится n – слоёв.

Коэффициент отражения: 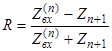где .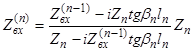

- входной импеданс системы, причём, если угол падения не равен нулю, то следует использовать:

ç

ç

при перпендикулярной и параллельной поляризациях соответственно.

Углы j рассчитывают исходя из законов Снелля.

Дата добавления: 2014-01-06