Прямоугольный металлический волновод

Прямоугольный металлический волновод

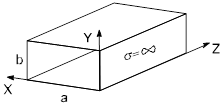это полая металлическая идеально проводящая () труба с поперечным сечением прямоугольной формы.

Будем полагать, что волновод заполнен средой с параметрами (воздух) 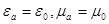. Найдем все типы электромагнитных волн, которые могут существовать внутри волновода на всем протяжении оси (как они созданы пока не рассматриваем).

Волны типа – H:

Для этих волн характерно . Тогда из системы (3.2):

; ;

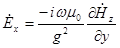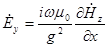; (3.3)

Где функция 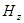является решением уравнения Гельмгольца (- производные только по поперечным координатам):

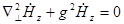, где и отыскивается в виде: .

При решении следует учитывать граничные условия (тангенциальная составляющая Е на металле обращается в 0):

при y = 0, y = b

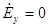при x = 0, x = а

При решении удобнее выразить их через :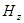

при у = 0, у = b

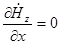при x = 0, x = а

Таким образом, надо решить краевую задачу Неймана (в ноль обращается производная, иначе Дирихле).

Используем метод Фурье, представляем 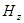в виде:

,

подставляем его в уравнение Гельмгольца:

,

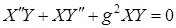разделим это уравнение на неизвестное решение:

.

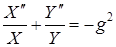g - не зависит от X и Y, поэтому, чтобы последнее уравнение выполнялось при всех X и Y, надо чтобы:

,,

где - некоторые числа удовлетворяющие: .

Общие решения двух последних уравнений выражаются через гармонические функции:

;

.

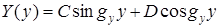Отсюда: .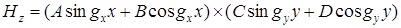

Остается выбрать шесть величин A, B, C, D, , так, чтобы выполнялись граничные условия на стенках волновода.

Граничные условия при X = 0 и Y = 0 будут выполнятся, если А = С = 0.

Произведение двух оставшихся амплитудных коэффициентов можно обозначить через и тогда:

.

Теперь остается подобрать величины 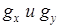так, чтобы граничные условия выполнялись при

X = а и Y = b:

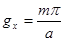; g;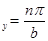

Где m и n – любые целые положительные числа не равные нулю одновременно (иначе силовые линии магнитного поля Н - незамкнуты и нарушается четвертое уравнение Максвелла).

Краевая задача имеет решения отличные от нуля только при условии:

.

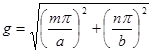Каждому значению g, (собственное значение) соответствует одно из множества решений уравнений Максвелла, которое в данном случае называют волной , где m и n – индексы волны данного типа. Физически они означают количества стоячих полуволн, возникающих внутри волновода вдоль координатных осей x и y соответственно.

Структура ЭМП волны типа

.

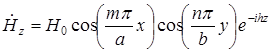Мы получили выражение для проекции 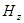, используем формулы перехода:

; .

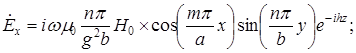
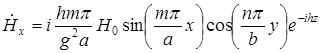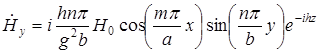Приведенная система формул содержит исчерпывающую информацию об электромагнитном поле волн типа . Картина поля периодична вдоль оси z; пространственным периодом служит длина волны в волноводе:

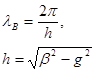
Если рабочая длина волны 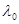мала настолько, что 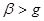, то h-действительна и электромагнитное колебание распространяется в виде бегущей волны постоянной амплитуды. Если увеличить 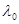так, что 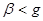, то вместо бегущих волн в волноводе могут существовать лишь не распространяющиеся колебания, амплитуда которых уменьшается по экспоненте вдоль z, а фаза во всех поперечных сечениях постоянна – волновод работает в режиме отсечки. Пограничный случай возникает на такой рабочей частоте, когда: .

При этом h = 0, , а длину волны генератора называют критической:

,

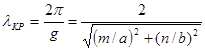соответственно:

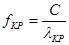(3.4)

Подставляем вместо 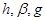их выражения: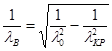

или

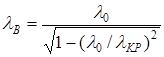(3.5)

Закон зависимости от 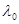называют дисперсионной характеристикой волновода, причем, т.к. эта характеристика найдена лишь при условии, что зависимость от z определяется exp(-ihz), и в предположении существования режима отсечки, то эта зависимость относится к волне любого типа в полом металлическом волноводе с любым сечением.

Отличия в определении . Изобразим дисперсионную характеристику.

До 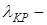область прозрачности т.к. следовательно:

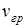определяем по общему правилу: 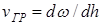, (3.6)

тогда .

Групповая скорость всегда меньше скорости света, причем для одного типа:

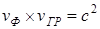(3.7)

на любой частоте.

Волна .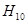

Для наглядного представления пространственной структуры поля построим картину силовых линий электрического и магнитного полей.

Критическая 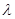при m = 1 n = 0 из формулы (3.4):

(3.8)

Подставим эти постоянные в выражения для составляющих поля волны .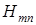

;

;

;

.

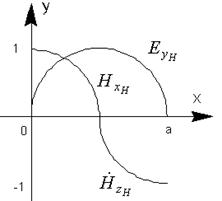
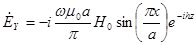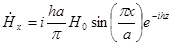Построим зависимости, нормированные на максимальные значения.

В поперечном сечении - стоячая волна и эта картина смещается вдоль z с фазовой скоростью.

1. Вид спереди. Для Е - концентрация в центре максимальна, а на боковых стенках – 0.

2. Силовые линии для Н должны быть замкнуты и зависимость от у – отсутствует.

Вид сверху.

Максимумы 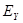и 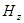сдвинуты в пространстве по фазе на 90(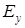и совпадают). Через каждые полдлины волны направление меняется.

В объеме для волныН-типа.

Вектор Пойнтинга, как следует из выражений для составляющих поля, имеет две составляющие -, но в среднем поле распространяется только вдоль оси z:

т.е. максимум энергии приходится на середину волновода.

Дата добавления: 2014-01-06